Zginanie proste belek

Zginanie proste belek
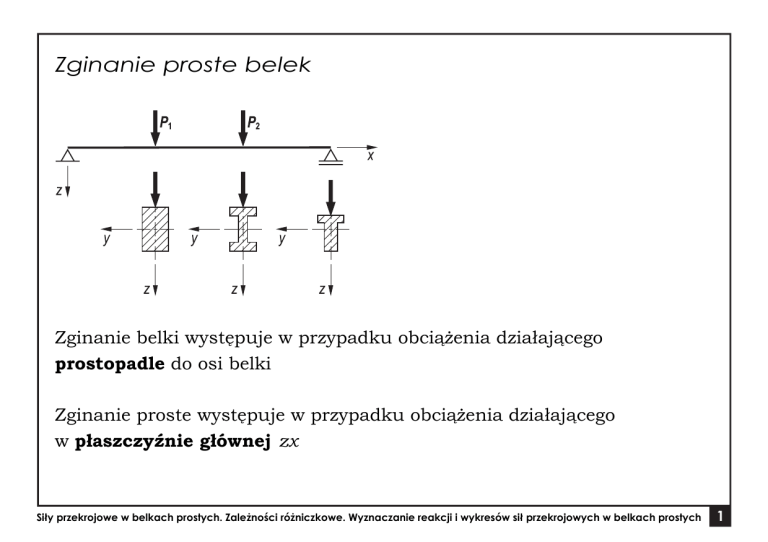
Zginanie belki występuje w przypadku obciążenia działającego
prostopadle do osi belki
Zginanie proste występuje w przypadku obciążenia działającego
w płaszczyźnie głównej zx
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
1
Zginanie proste belek
Rozpatrzmy belkę swobodnie podpartą o przekroju prostokątnym
obciążoną siłą skupioną P w środku rozpiętości
h≤
l
10
Hipoteza Bernoulli’ego:
Przekroje poprzeczne pozostają
płaskie i prostopadłe do osi
odkształconej belki
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
2
Zginanie proste belek
Rodzaje obciążeń
Obciążenie belki mogą stanowić:
— siły skupione P [N]
— momenty skupione M [N·m]
— obciążenia ciągłe q [N/m]
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
3
Zginanie proste belek
Wartość reakcji określamy wykorzystując równania równowagi statycznej:
ΣPix = 0
(5.1a)
ΣPiz = 0
(5.1b)
ΣM i = 0
(5.1c)
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
4
Zginanie proste belek
Wielkości przekrojowe:
Siła tnąca (poprzeczna) T — w danym przekroju jest sumą rzutów
sił zewnętrznych działających po jednej stronie rozpatrywanego przekroju
na kierunek styczny do przekroju.
Moment gnący (zginający) M — w danym przekroju jest sumą momentów
obciążeń zewnętrznych działających po jednej stronie rozpatrywanego
przekroju względem środka masy tego przekroju.
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
5
Zginanie proste belek
Zależności różniczkowe
ΣPiz = 0 :
− T + q ⋅ dx + T + dT = 0
dT
= −q
dx
(5.2)
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
6
Zginanie proste belek
Zależności różniczkowe
ΣM iC = 0 :
− M + (M + dM ) − (T + dT ) ⋅ dx − (q ⋅ dx ) ⋅
dM
=T
dx
dx
=0
2
(5.4)
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
7
Zginanie proste belek
Wyznaczanie wykresów sił przekrojowych
— metoda przepisów funkcyjnych
— metoda rzędnych charakterystycznych
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
8
Zginanie proste belek
Wyznaczanie wykresów sił przekrojowych
— metoda przepisów funkcyjnych
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
9
Zginanie proste belek
Wyznaczanie wykresów sił przekrojowych
— metoda przepisów funkcyjnych
odcinek AB: 0 ≤ x ≤ l
siła tnąca
T ( x ) = R Az
moment gnący
M ( x ) = R Az ⋅ x
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
10
Zginanie proste belek
Wyznaczanie wykresów sił przekrojowych
— metoda przepisów funkcyjnych
odcinek BC: l ≤ x ≤ 2l
siła tnąca
T (x ) = R Az − P1
moment gnący
M (x ) = R Az ⋅ x − P1 ⋅ (x − l )
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
11
Zginanie proste belek
Wyznaczanie wykresów sił przekrojowych
— metoda przepisów funkcyjnych
odcinek CD: 2l ≤ x ≤ 3l
siła tnąca
T (x ) = R Az − P1 − P2
moment gnący
M (x ) = R Az ⋅ x − P1 ⋅ (x − l ) − P2 ⋅ (x − 2l )
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
12
Zginanie proste belek
Wyznaczanie wykresów sił przekrojowych
— metoda rzędnych charakterystycznych
siły tnące (od lewej strony)
TAB = R Az
TBC = R Az − P1
TCD = R Az − P1 − P2
siły tnące (od prawej strony)
TCD = −RDz
TBC = −RDz + P2
TAB = −RDz + P2 + P1
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
13
Zginanie proste belek
Wyznaczanie wykresów sił przekrojowych
— metoda rzędnych charakterystycznych
momenty gnące (od lewej strony)
MA = 0
M B = R Az ⋅ l
M C = R Az ⋅ 2l − P1 ⋅ l
M D = R Az ⋅ 3l − P1 ⋅ 2l − P2 ⋅ l = 0
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
14
Zginanie proste belek
Wyznaczanie wykresów sił przekrojowych
— metoda rzędnych charakterystycznych
momenty gnące (od prawej strony)
MD = 0
M C = RDz ⋅ l
M B = RDz ⋅ 2l − P2 ⋅ l
M A = RDz ⋅ 3l − P2 ⋅ 2l − P1 ⋅ l = 0
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
15
Zginanie proste belek
Cechy charakterystyczne wykresów sił przekrojowych
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych
16
BIBLIOGRAFIA
Dyląg Z., Jakubowicz A., Orłoś Z., Wytrzymałość materiałów, tom I, WNT,
Warszawa 1999.
Klasztorny M., Skrypt do wytrzymałości materiałów [w przygotowaniu].
Siły przekrojowe w belkach prostych. Zależności różniczkowe. Wyznaczanie reakcji i wykresów sił przekrojowych w belkach prostych