laboratorium techniki cieplnej

LABORATORIUM TECHNIKI CIEPLNEJ
INSTYTUTU TECHNIKI CIEPLNEJ
WYDZIAŁ INŻYNIERII ŚRODOWISKA
I ENERGETYKI
POLITECHNIKI ŚLĄSKIEJ
INSTRUKCJA LABORATORYJNA
Temat ćwiczenia:
WYZNACZANIE WSPÓŁCZYNNIKA WNIKANIA CIEPŁA
DLA KONWEKCJI WYMUSZONEJ W RURZE
Wyznaczanie współczynnika wnikania ciepła dla konwekcji wymuszonej w rurze
OZNACZENIA
Gr – bezwymiarowa liczba Grashoffa,
Nu – bezwymiarowa liczba Nusselta
Pr – bezwymiarowa liczba Prandtla
Re – bezwymiarowa liczba Reynoldsa
a – współczynnik przewodzenia temperatury,m2/s
g – przyspieszenie ziemskie, m/s2
L – wymiar charakterystyczny powierzchni, m
q& – gęstość strumienia ciepła, W/m2
∆T – różnica temperatury ścianki i płynu, K
Tp – średnia temperatura płynu, K
Ts – średnia temperatura ścianki, K
w – średnia prędkość płynu, m/s
c – pojemność cieplna właściwa płynu, J/(kg K)
α – konwekcyjny współczynnik wnikania ciepła, W/(m2K)
β – współczynnik rozszerzalności objętościowej, K-1
λ – współczynnik przewodzenia ciepła, W/(m K)
ν - kinematyczny współczynnik lepkości płynu, m2/s
Instrukcja laboratoryjna
LABORATORIUM TECHNIKI CIEPLNEJ
2
Wyznaczanie współczynnika wnikania ciepła dla konwekcji wymuszonej w rurze
1.
3
PODSTAWY TEORETYCZNE
Konwekcja polega na przekazywaniu ciepła od ścianki do omywającego ją płynu lub
odwrotnie. Na intensywność konwekcyjnego strumienia ciepła duży wpływ ma prędkość
przepływającego płynu. Konwekcyjna wymiana ciepła charakteryzowana jest za pomocą
współczynnika wnikania (przejmowania) ciepła α określającego globalny efekt zjawiska, tzn.
związek między gęstością strumienia ciepła wymienianego przez ściankę z płynem a różnicą
temperatury powierzchni i płynu:
q& = α ⋅ ∆T
(1)
Celem niniejszego ćwiczenia jest poznanie podstawowych zależności występujących przy
konwekcji wymuszonej. Rozróżnia się dwa przypadki:
1- czynnik płynie wewnątrz kanału,
2- czynnik omywa z zewnątrz powierzchnię wymieniającą ciepło.
Ponadto przepływ czynnika może być uwarstwiony (laminarny), przejściowy lub burzliwy
(turbulentny ).
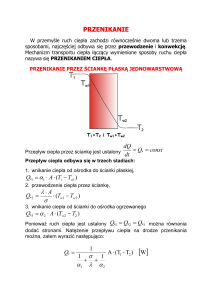
Analiza przepływu ciepła przez konwekcję sprowadza się zazwyczaj do określenia
współczynnika wnikania ciepła, który w postaci bezwymiarowej przedstawia liczba Nusselta:
Nu =
α⋅L
.
λ
(2)
Liczbę Nusselta możemy wyrazić w zależności od innych liczb bezwymiarowych: Reynoldsa,
Prandtla, Grashoffa:
Nu = f (Re, Pr, Gr ) .
(3)
Liczba Reynoldsa decyduje o charakterze przepływu:
Re =
w ⋅L
ν
(4)
Liczba Grashoffa uwzględnia samoistny ruch płynu spowodowany zmianą jego gęstości:
Gr =
β ⋅ g ⋅ ∆T ⋅ L3
,
ν2
(5)
gdzie:
∆T = Ts – Tp,
(6)
Dla gazów doskonałych
β=
1
.
T
(7)
Pr =
ν
,
a
(8)
λ
.
cρ
(9)
Liczba Prandtla opisuje własności płynu:
gdzie:
a=
Instrukcja laboratoryjna
LABORATORIUM TECHNIKI CIEPLNEJ
Wyznaczanie współczynnika wnikania ciepła dla konwekcji wymuszonej w rurze
4
Dla przepływu laminarnego słuszna jest zależność (3), gdzie liczba Grashoffa uwzględnia
ruch swobodny, którego wpływ jest w niektórych przypadkach znaczny. Dla przepływu
burzliwego wpływ ruchu swobodnego jest znikomy i równanie kryterialne przybiera postać:
Nu = f (Re, Pr ) .
(10)
W celu uwzględnienia dodatkowych czynników, nie dających się ująć w ramy liczb
kryterialnych wprowadza się do równań poprawki. Uwzględniają one między innymi:
- zwiększenie się średniej wartości współczynnika wnikania ciepła na tzw. odcinku
rozbiegowym – εl,
- wpływ kierunku przepływu ciepła (od ścianki do płynu lub odwrotnie) – εt,
- wpływ krzywizny kanału przepływu – εr.
2.
WYZNACZANIE KONWEKCYJNEGO
CIEPŁA NA DRODZE TEORETYCZNEJ
WSPÓŁCZYNNIKA
WNIKANIA
Liczbę Nusselta (Nu) wyznacza się na podstawie równania kryterialnego. W przypadku
konwekcji wymuszonej przy przepływie czynnika wewnątrz kanału o przekroju kołowym
równania kryterialne mają postać:
a) przepływ laminarny (Re < 24001)
Nu = 0.17 ⋅ Re 0.33 ⋅ Gr 0.1 ⋅ Pr 0.43 ⋅ ε t ⋅ ε l ,
(11)
b) przepływ przejściowy (2400 ≤ Re ≤ 10 000)
Nu = K 0 ⋅ Pr 0.43 ⋅ ε t ⋅ ε l ,
Re·10
K0
-3
2.2
2.2
2.3
3.6
2.5
4.9
3.0
7.5
K 0 = f (Re )
3.5
4.0
5.0
10.0 12.2 16.5
(12)
6.0
20.0
7.0
24.0
8.0
27.0
9.0
30.0
10.0
33.0
c) przepływ turbulentny (Re > 10 000)
Nu = 0.021 ⋅ Re 0.8 ⋅ Pr 0.43 ⋅ ε t ⋅ ε l .
(13)
Po wyznaczeniu wartości liczby (Nu) wartość konwekcyjnego współczynnika wnikania ciepła
α wyznacza się z równania (2), które po przekształceniu ma postać:
α = Nu
λ
.
L
(14)
Wartości liczb kryterialnych oraz własności płynu wyznacza się dla średniej temperatury
płynu Tp.
Poprawkę εl oblicza się z zależności:
 Prp 

ε t = 
 Prs 
0.25
,
1
(15)
UWAGA: w literaturze podawane są różne wartości granicznej liczby Reynoldsa dla przepływu laminarnego;
zakres tych wartości – 2000 ... 3000, chociaż wartość Re = 2400 pojawia się najczęściej.
Instrukcja laboratoryjna
LABORATORIUM TECHNIKI CIEPLNEJ
Wyznaczanie współczynnika wnikania ciepła dla konwekcji wymuszonej w rurze
5
gdzie Prp i Prs oznaczają wartości liczby Prandtla wyznaczone dla temperatury płynu Tp i
ścianki Ts.
Wartość poprawki εl zależy od wartości Re oraz stosunku długości do średnicy kanału. W
powyższych obliczeniach można przyjąć εl = 1.0
Własności fizyczne suchego powietrza konieczne przy obliczaniu wartości liczb kryterialnych
podano w załączniku do instrukcji.
3.
WYZNACZANIE KONWEKCYJNEGO
CIEPŁA NA DRODZE POMIARÓW
WSPÓŁCZYNNIKA
WNIKANIA
3.1 Stanowisko pomiarowe
Głównym elementem stanowiska pomiarowego (rys.1) jest rura przepływowa 1, na którą
nawinięta jest grzałka elektryczna 2. Całość jest zaizolowana termicznie 3. Temperatura gazu
oraz ścianki rurki mierzona jest za pomocą termopar NiCr-Ni. Przełącznik miejsc
pomiarowych 7 może działać w trybie automatycznym lub ręcznym. Wskaźnik temperatury 8
wyposażony jest układ przeliczający wartość siły termolelektrycznej z termoelementów na
różnicę temperatury oraz układ mierzący temperaturę otoczenia. Z tego powodu odczytywana
z wyświetlacza wartość jest wprost wartością temperatury w danym punkcie pomiarowym.
Powietrze jest dostarczane z instalacji sprężarkowej 11, a natężenie jego przepływu jest
regulowane zaworem 10 i mierzone rotametrem 9.
o
C
9
11
4
7
6
8
5
3
12
10
1
2
Rys. 1 Schemat stanowiska pomiarowego
1 – rura przepływowa, 2 – grzałka elektryczna, 3 – izolacja, 4 – termopara mierząca
temperaturę gazu na dolocie, 5 – termopara mierząca temperaturę gazu na wylocie,
6 – termopary mierzące temperaturę ścianki rurki, 7 – przełącznik miejsc pomiarowych,
8 – wskaźnik temperatury, 9 – rotametr, 10 – zawór regulacyjny natężenia przepływu,
11 – instalacja sprężonego powietrza, 12 – osłona
3.2 Opis pomiarów
Układ pomiarowy należy każdorazowo doprowadzić do stanu ustalonego. Sprawdzianem
osiągnięcia tego stanu jest niezmienność temperatury powietrza i ścianki rury przepływowej.
Instrukcja laboratoryjna
LABORATORIUM TECHNIKI CIEPLNEJ
Wyznaczanie współczynnika wnikania ciepła dla konwekcji wymuszonej w rurze
6
Pomiary należy przeprowadzić dla przepływu burzliwego, przejściowego oraz laminarnego.
Przepływy te uzyskuje się przez odpowiednią regulację wydajności przepływu powietrza
przez ogrzewaną rurę. Wartości przepływu zostaną podane przed ćwiczeniem.
W czasie ćwiczenia należy zwracać szczególną uwagę na stabilność przepływu. Wszelkie
znaczące odchylenia od ustalonej wartości należy korygować za pomocą zaworu
regulacyjnego.
3.2 Przebieg ćwiczenia
Wielkości mierzone:
V& p - strumień powietrza,
tp1, tp2 – temperatura powietrza dopływającego i wypływającego z rury,
ts1, ts2 – temperatura powierzchni ścianki rury przepływowej.
Odczytu temperatury należy dokonać po dostatecznym przybliżeniu stanu ustalonego,
tzn. po ustaleniu się wskazań temperatury we wszystkich punktach pomiarowych co trwa
około 20 minut. W tym czasie należy notować wszystkie wskazania w odstępach czasu
zadanych przez prowadzącego. Po zakończeniu każdego pomiaru należy odczytać wartości
temperatury otoczenia (termometr szklany naścienny) oraz ciśnienia otoczenia (barometr).
3.3 Obliczenie rzeczywistego strumienia powietrza
Strumień gazu odczytuje się na rotametrze, który jest wycechowany w działkach dla
powietrza o temperaturze tn = 20ºC i ciśnieniu pn = 101325 Pa. Aby określić objętość
strumienia powietrza należy skorzystać z charakterystyki rotametru, z której odczytuje się
& w m3/h. Ponieważ w pomieszczeniu laboratoryjnym z reguły panują
natężenie przepływu V
n
warunki nieco różniące się od warunków znamionowych rotametru należy zredukować
odczytaną z charakterystyki wartość do warunków rzeczywistych. Można to zrobić zapisując
równanie stanu Clapeyrona dla warunków znamionowych i warunków rzeczywistych. Po
uproszczeniu otrzymuje się:
T p
V& p = V&n ot n
(16)
Tn p
& - odczyt z charakterystyki rotametru,
V
n
V& - rzeczywisty strumień gazu,
p
T ot - temperatura otoczenia, K
Tn - temperatura znamionowa dla rotametru, 293.15 K
p - ciśnienie bezwzględne na dolocie do rury przepływowej, p = p ot + ∆p (przyrost
ciśnienia w dmuchawie, podaje prowadzący ćwiczenie)
p n - ciśnienie znamionowe dla rotametru, 101325 Pa
Masę strumienia powietrza oblicza się z zależności:
G& = V& p ⋅ ρ ,
(17)
przy czym gęstość gazu ρ określa się w oparciu o tablice własności powietrza dla temperatury
Tot lub oblicza z równania Clapeyrona dla parametrów na dolocie do rury przepływowej. Do
obliczeń masę strumienia powietrza G& należy wyrazić w kg/s.
Instrukcja laboratoryjna
LABORATORIUM TECHNIKI CIEPLNEJ
Wyznaczanie współczynnika wnikania ciepła dla konwekcji wymuszonej w rurze
7
Średnią prędkość powietrza przepływającego przez rurę wyznacza się z zależności:
w=
4 ⋅ V& p
Πd 2
(18)
,
gdzie przez d oznaczono średnicę wewnętrzną rury (d = 9 mm).
3.4 Opracowanie wyników pomiarów
Z bilansu energii dla stanu ustalonego wynika zależność:
Q& g = Q& p + Q& ot ,
(19)
gdzie:
Q& g - strumień ciepła wytwarzanego przez grzejnik,
Q& - strumień ciepła pochłaniany przez przepływające powietrze,
p
Q& ot - strumień ciepła tracony na rzecz otoczenia.
W celu wyznaczenia współczynnika wnikania ciepła należy znać strumień ciepła
pochłoniętego przez powietrze. Strumień Q& p wyznacza się z zależności:
Q& p = G& p c p (T p 2 − T p1 ) .
(20)
Wykorzystując równanie (1) strumień Q& p można wyrazić zależnością:
Q& p = F ⋅ q& = F ⋅ α ⋅ (Ts − T p ) .
(21)
Z równań (18) i (19) wynika:
α=
G& p c p (T p 2 − T p1 )
F (Ts − T p )
,
(22)
gdzie:
Ts, Tp – średnie wartości temperatury ścianki i płynu:
Ts =
Ts1 + Ts 2
2
Tp =
T p1 + T p 2
2
cp – ciepło właściwe przy stałym ciśnieniu w warunkach pomiaru,
F = Πdl – pole powierzchni wymiany ciepła (d = 9 mm, l = 960 mm).
4.
SPRAWOZDANIE
Sprawozdanie powinno zawierać:
- krótkie wprowadzenie teoretyczne, zawierające w szczególności charakterystykę
wyznaczanej wielkości oraz opis metody pomiarowej,
- cel ćwiczenia,
- schemat stanowiska pomiarowego,
- zestawienie wzorów i zależności wykorzystanych w obliczeniach (nie należy powtarzać
wzorów jeżeli pojawiły się we wstępie),
- zestawienie wyników pomiarów dla stanu ustalonego,
- tablice wartości α otrzymanych z obliczeń przy użyciu wzorów kryterialnych i pomiarów,
Instrukcja laboratoryjna
LABORATORIUM TECHNIKI CIEPLNEJ
Wyznaczanie współczynnika wnikania ciepła dla konwekcji wymuszonej w rurze
-
8
wykres zależności α = α(w),
analizę dokładności otrzymanych wyników i przyczyn ewentualnych różnic, uwagi na
temat metody pomiarów.
UWAGI:
1. W przypadku analizy konwekcyjnej wymiany ciepła dla przypadku przepływu
czynnika wewnątrz kanału jako wymiar charakterystyczny zawsze przyjmuje się
średnicę wewnętrzną dla kanałów o przekroju okrągłym lub tzw. średnicę
ekwiwalentną dla kanałów o innych przekrojach.
2. Jeżeli obliczona wartość liczby Reynoldsa zbliżona jest do wartości granicznych
pomiędzy dwoma rodzajami przepływu, zalecane jest obliczenie wartości
konwekcyjnego współczynnika wnikania ciepła z zależności dla obu graniczących
rodzajów przepływów (np. Re = 9500 – liczymy α raz traktując przepływ jako
przejściowy, drugi raz traktując przepływ jako burzliwy).
LITERATURA
[1] Kostowski E.: Przepływ ciepła. Skrypt Politechniki Śląskiej nr 1293, Gliwice 1989.
Instrukcja zaktualizowana 27.02.2004
Instrukcja laboratoryjna
LABORATORIUM TECHNIKI CIEPLNEJ
Wyznaczanie współczynnika wnikania ciepła dla konwekcji wymuszonej w rurze
9
Załącznik 1
WŁASNOŚCI FIZYCZNE POWIETRZA SUCHEGO
PRZY CIŚNIENIU p = 0.101 MPa
T
ρ
cp
λ·102
a·106
ν·106
Pr
K
kg/m3
kJ/(kg·K)
W/(m·K)
m2/s
m2/s
-
273
1,293
1,005
2,44
18,8
13,28
0,707
283
1,247
1,005
2,51
20,0
14,16
0,705
293
1,205
1,005
2,59
21,4
15,06
0,703
303
1,165
1,005
2,67
22,9
16,00
0,701
313
1,128
1,005
2,76
24,3
16,96
0,699
323
1,093
1,005
2,83
25,7
17,95
0,698
333
1,060
1,005
2,90
27,2
18,97
0,696
343
1,029
1,009
2,96
28,6
20,02
0,694
353
1,000
1,009
3,05
30,2
21,09
0,692
363
0,972
1,009
3,13
31,9
22,10
0,690
373
0,946
1,009
3,21
33,6
23,13
0,688
Instrukcja laboratoryjna
LABORATORIUM TECHNIKI CIEPLNEJ