Część IV: Optyczne metody badania oddziaływań
Biofizyka II
przedmiot obieralny
Materiały pomocnicze do wykładów
prof. dr hab. inż. Jan Mazerski
4. OPTYCZNE METODY BADANIA ODDZIAŁYWAŃ
Efekt oddziaływania promieniowania elektromagnetycznego z materią zależy od energii
kwantu tego promieniowania.
Energia pojedynczego kwantu promieniowanie γ i X wynosi powyżej 10 eV, a
tym samym przekracza energię jonizacji wiekszosci substancji organicznych.
Dlatego
promieniowanie
takie
wywołuje
w
układach
biologicznych
występowanie procesu jonizacji.
Kwant światło z obszaru widzialnego i bliskiego nadfioletu ma za mało energii, ok. 1 ev, aby
całkowicie oderwać elektron od cząsteczki. Ma go jednak dostatecznie dużo, aby
przenieść elektron na wyższy poziom energetyczny. Energia niezbędna do
wzbudzenia elektronowego zależy od budowy chemicznej cząsteczki. Z reguły
wzbudzeniu ulegają tylko niektóre fragmenty cząsteczki zwane chromoforami.
Typowe wzbudzenia elektronowe w związkach organicznych dotyczą przejść
π→π* lub n→π.
Promieniowanie podczerwone ma jeszcze niższą energię pojedynczego kwantu, ok. 0,1 eV. Energia ta
wystarcza jedynie do przeniesienia cząsteczki na wyższy poziom oscylacyjny bez
wywołania wzbudzenia elektronowego. Energia wzbudzenia oscylacyjnego zależy od
rodzaju atomów tworzących wiązanie oraz od siły wiązania. Najłatwiej ulegają wzbudzeniu wiązania,
w których jednym z partnerów jest atom wodoru.
Ostatnim rodzajem promieniowania zdolnym do wzbudzenia cząsteczek jest promieniowanie
mikrofalowe. Pojedynczy kwant tego promieniowania ma energię rzędu 0,01 eV i jest
w stanie przenieść małe cząsteczki organiczne lub nieorganiczne na wyższy poziom
rotacyjny.
Warto przy tym pamiętać, że zmiana poziomu energetycznego cząsteczki związana jest z
absorpcją lub emisją kwantu o energii dokładnie równej różnicy poziomów energetycznych całej
cząsteczki. Energię cząsteczki można z rozsądnym przybliżeniem traktować jako sumę energii:
stanów elektronowych, Eel,
stanów oscylacyjnych, Eos, i
stanów rotacyjnych, Erot.
1
Część IV: Optyczne metody badania oddziaływań
W temperaturze pokojowej cząsteczki znajdują się w podstawowym stanie elektronowym i
oscylacyjnym oraz na jednym ze wzbudzonych stanów rotacyjnych. Wzbudzenie elektronowe
związane może być ze wzbudzeniem oscylacyjnym i rotacyjnym, a wzbudzenie oscylacyjne ze
wzbudzeniem rotacyjnym. Dlatego nie można uzyskać czystego widma elektronowego lub
oscylacyjnego.
4.1 Widma elektronowe
Prawdopodobieństwo wystąpienia absorpcji lub emisji światła związanego ze zmianą stanu
elektronowego cząsteczki zależne jest od wartości tak zwanego momentu przejścia, Mmn:
M mn = ∫ ψ*m Mψ n dV
gdzie: ψn – cząsteczkowa funkcja falowa stanu podstawowego,
ψ*m – cząsteczkowa funkcja falowa stanu wzbudzonego,
M – moment dipolowy cząsteczki.
Przejście elektronowe jest tym bardziej prawdopodobne, im większy jest moment przejścia. Gdy
Mmn = 0 mamy do czynienia z tzw. przejściami wzbronionymi. Wzbronione są np. przejścia związane
ze zmianą multipletowości stanu (synglet → tryplet lub odwrotnie). Jednakże w skomplikowanych
cząsteczkach organicznych przejścia wzbronione mają niezerowe prawdopodobieństwo wystąpienia.
Wynikać to może z powodu występowania:
sprzężenia spinu elektronów z ich orbitalnym momentem pędu (tzw. sprzężeń spin – orbita),
kwadrupolowego momentu dipolowego, lub
magnetycznego momentu dipolowego.
Zawsze jednak prawdopodobieństwo przejść wzbronionych jest mniejsze niż przejść dozwolonych,
czasami nawet o rzędy wielkości.
4.1.1 Diagram Francka-Condona
Wygodnym narzędziem pozwalającym na analizę widm elektronowych jest tak zwany diagram
Francka-Condona. Pozwala on zrozumieć położenie pasm zarówno w widmach absorpcyjnych jak i
emisyjnych (fluorescencja). Oś pionowa diagramu repreze ntuje energię, a oś pozioma odległość
atomów tworzących chromofor. Linie krzywe na diagramie przedstawiają przebieg zmian całkowitej
energii
cząsteczki
w
funkcji
odległości
odpowiednio
dla
podstawowego
stanu
elektronowego(niebieska linia na rysunku poniżej) oraz najbliższego elektronowego stanu
wzbudzonego (linia czerwona).
Dla każdego ze stanów elektronowych zaznacza się ponadto jego poziomy oscylacyjne (cienkie linie
poziome w obrębie studni energii). Wzbudzenie elektronowe zachodzi tak szybko, że pozycja jąder nie
zdąży ulec zmianie. Na diagramie odpowiada to tzw. przejściu pionowemu. Przejście elektronowe
2
Część IV: Optyczne metody badania oddziaływań
zachodzi najczęściej ze stanu najbardziej prawdopodobnego, czyli środka najniższego poziomu
oscylacyjnego.
Istnieje jednak niezerowe prawdopodobieństwo przejścia również z któregoś ze wzbudzonych stanów
oscylacyjnych. Dla stanów takich najbardziej prawdopodobne jest występowanie układu w tzw.
punktach zwrotnych, czyli z krańców poziomów oscylacyjnych.
Rozważmy np. absorpcję kwantu z podstawowego stanu oscylacyjnego (szara strzałka pionowa
na wykresie powyżej). Ponieważ krzywe energii są przesunięte względem siebie, więc przejście
pionowe z najbardziej prawdopodobnego stanu podstawowego kończy się zarówno na stanie
wzbudzonym elektronowo jak i oscylacyjnie. Analogicznie, emisja światła z najbardziej
prawdopodobnego elektronowego stanu podstawowego (zielona strzałka) kończy się na podstawowym
stanie elektronowym, ale wzbudzonym stanie oscylacyjnym. Z powyższych rozważań wynika, że:
struktura oscylacyjna widma absorpcyjnego dostarcza informacji o poziomach oscylacyjnych
stanu wzbudzonego, a
struktura oscylacyjna widma emisyjnego o poziomach oscylacyjnych stanu podstawowego.
4.1.2 Elektronowe widmo absorpcyjne
Absorpcję promieniowania elektromagnetycznego w zakresie widzialnym i bliskim nadfiolecie
opisuje prawo Lamberta-Beera:
I = I 0e −ε (λ )cd
gdzie: I i I0 to odpowiednio natężenie po i przed próbką
c – stężenie molowe substancji absorbującej
d – grubość warstwy roztworu
ε(λ) – molowy współczynnik ekstynkcji
3
Część IV: Optyczne metody badania oddziaływań
W codziennym użyciu wygodniejsza jest logarytmiczna postać tego prawa:
A = ln
I0
= ε(λ )cd
I
będąca jednocześnie definicja wielkości zwanej absorbancją.
Molowy współczynnik ekstynkcji
Molowy współczynnik ekstynkcji jest funkcją długości fali, a jego wielkość zależy od:
rodzaju przejścia elektronowego
budowy chemicznej związku
lokalnego otoczenia chromoforu
Pojedyncze pasmo absorpcyjne opisujemy zgrubnie podając ekstynkcje molową w maksimum pasma,
ε(λmax). Jej wartość zależy przede wszystkim od rodzaju przejścia elektronowego:
silne pasma dozwolone (duża zmiana momentu dipolowego) ε(λmax) > 104
słabe pasmo dozwolone ε(λmax) ≈ 103
pasmo zabronione ε(λmax) < 100
Lokalne otoczenie chromoforu
W badaniach biofizycznych nie interesuje nas zwykle szczegółowe poznanie struktury
poziomów energetycznych substancji, a raczej wpływ otoczenia chromoforu na jego widmo.
Położenie, natężenie, a przede wszystkim kształt pasma absorpcyjnego zależy w znacznym stopniu od
lokalnego otoczenia chromoforu. Lokalnym otoczeniem chromoforów w układach biologicznych
mogą być cząsteczki rozpuszczalnika lub fragmenty biopolimeru. Tym samym chromofor może pełnić
rolę sondy pozwalającej na określenie właściwości jego najbliższego otoczenia.
Pomiędzy chromoforem a jego otoczeniem występują oddziaływania, które prowadzą do
powstania lokalnego uporządkowania cząsteczek rozpuszczalnika lub fragmentów biopolimeru.
Charakter, zasięg i stopień tego uporządkowania zmienia się po przejściu ze stanu podstawowego w
stan wzbudzony. Uporządkowanie jak i jego zmiany w wyniku wzbudzenia zależą przy tym bardzo
silnie od właściwości środowiska lokalnego. Np. położenie i kształt długofalowego pasma
absorpcyjnego chromoforu indolowego w łańcuchu bocznym tryptofanu silnie zależy od tego, czy
znajduje się on w otoczeniu hydrofilowym (na powierzchni białka w kontakcie z wodą) czy
hydrofobowym (wewnątrz cząsteczki białka).Ponadto z wielkości i kierunku zmian położenia pasma
absorpcyjnego przy zmianie polarności środowiska wyciągnąć można wnioski na temat rodzaju
przejścia odpowiedzialnego za powstanie pasma. W przypadku przejścia π→π* wzrost polarności
środowiska powoduje przesunięcie pasma w kierunku fal dłuższych. Odwrotnie zachowuje się pasmo
związane z przejściem n→π*.
Wykazano, że położenie maksimum pojedynczego pasma absorpcji zależy od:
położenia maksimum absorpcji w próżni, λmax0
4
Część IV: Optyczne metody badania oddziaływań
momentu dipolowego chromoforu, M
względnej stałej dielektrycznej lokalnego otoczenia chromoforu, ε
lokalnej wartości współczynnika załamania światła.
Aktualne położenie pasma można wyznaczyć, że wzoru:
λ max = λ max 0 −
2M 2
hc
⎡ ε −1
n 2 −1 ⎤
−
⎢
⎥.
⎢⎣ 2ε + 1 2(2n + 1) ⎥⎦
W biofizyce zależność powyższa bywa raczej wykorzystywana do wyznaczania parametrów lokalnego
otoczenia chromoforu, np. współczynnika załamania światła.
4.1.3 Elektronowe widmo emisyjne (fluorescencja)
W wyniku absorpcji kwantu promieniowania o odpowiedniej
energii cząsteczka znajdująca się na podstawowym poziomie
elektronowym i podstawowym poziomie oscylacyjnym przechodzi do
wzbudzonego stanu elektronowego. Jak już mówiliśmy przejście to ma
charakter przejścia pionowego na diagramie Francka-Condona, a więc
odbywa się bez zmiany geometrii cząsteczki. Oznacza to, że
chromofor „trafia” na jeden ze wzbudzonych stanów oscylacyjnych
wzbudzonego stanu elektronowego (linia żółta na wykresie obok). W tym stanie zderza się z
cząsteczkami ze swego otoczenia oraz uczestniczy w drganiach całej cząsteczki. Na skutek tych
oddziaływań może oddać energię wzbudzenia oscylacyjnego na drodze przejść bezpromienistych.
Najczęściej odbywa się to w kilku etapach.
W ten sposób chromofor „schodzi” po drabinie poziomów
oscylacyjnych (czerwone strzałki) aż do podstawowego stanu
oscylacyjnego wzbudzonego stanu elektronowego (zielona linia).
Bezpromieniste przejście pomiedzy stanami elektronowymi jest
bardzo mało prawdopodobne ze względu na dużą różnice poziomów
energetycznych. W efekcie chromofor pozostaje przez czas rzędu
milisekund we wzbudzonym stanie elektronowym.
Zwykle opuszcza ten stan na drodze emisji kwantu promieniowania
(zielone strzałki na rysunku obok). Zjawisko to nazywamy
fluorescencją. Fluorescencja, podobnie jak absorpcja, jest przejściem
pionowym i układ po emisji zatrzymać się może na jednym z kilku
stanów oscylacyjnych podstawowego stanu elektronowego. Dlatego
też widmo fluorescencyjne posiada również strukturę oscylacyjną.
5
Część IV: Optyczne metody badania oddziaływań
Kształt widm emisyjnych i absorpcyjnych
Na widmo absorpcyjne składają się kolejno przejścia: 0→0*, 0→1*, 0→2* itd. Przejściom tym
odpowiada coraz większa energia, więc występują one przy coraz krótszych długościach fali (lewy
panel na rysunku poniżej).
Widmo fluorescencyjne powstaje w wyniku przejść 0*→0, 0*→1, 0*→2 itd. Ponieważ przejścia
kończą się na coraz wyższych poziomach oscylacyjnych, więc na widmie występują przy coraz
większych długościach fali (panel prawy).
widmo
absorpcji
widmo
emisji
Można oczekiwać, że przejście 0→0* w widmie absorpcyjnym i przejście 0*→0 w widmie emisyjnym
powinny się pokrywać. Zwykle jednak występuje pomiędzy nimi niewielka różnica (rysunek poniżej).
Związane jest to z różnym otoczeniem chromoforu w stanie podstawowym i wzbudzonym.
widmo
absorpcji
widmo
emisji
Absorpcja
(szybko)
Emisja
(szybko)
W stanie podstawowym chromofor (szary prostokąt) znajduje się w otoczeniu dopasowanym do
geometrii i rozkładu elektronowego tego stanu (szara elipsa). Absorpcja kwantu zachodzi tak szybko,
że wzbudzony stan elektronowy (zielony równoległobok) początkowo znajduje się w niedopasowanym
do niego otoczeniu. Po pewnym czasie otoczenie dopasowuje się do wzbudzonego stanu
elektronowego (zielona elipsa). Emisja kwantu jest również bardzo szybka, więc powstający
elektronowy stan podstawowy znajduje się początkowo w otoczeniu dopasowanym do stanu
wzbudzonego. Tak więc przejścia 0→0* i 0*→0 nie są sobie równoważne.
Przesuniecie stokesowskie
6
Część IV: Optyczne metody badania oddziaływań
Ponieważ emisja kwantu zachodzi z niższego poziomu en ergetycznego (część energii została
rozproszona na drzodze przejść bezpromienistych), więc
(λ max)abs
(λmax)em
widmo fluorescencji jest przesunięte w stosunku do widma
absorpcji
w
kierunku
większych
długości
fali:
(λmax)em > (λmax)abs. Przesuniecie to nosi nazwę przesunięcia
stokesowskiego. Jego wielkość zależna jest przy tym bardzo
silnie od właściwości lokalnego otoczenia chromoforu.
Wzbudzenie elektronowe związane jest zwykle ze wzrostem
momentu dipolowego chromoforu, więc towarzyszy mu:
polaryzacja chmur elektronowych cząsteczek otaczających chromofor
przesunięcie indukcyjne atomów
polaryzacja orientacyjna
Tak więc przesunięcie stokesowskie będzie tym większe im:
dłuższy będzie czas życia stanu wzbudzonego,
większa będzie przenikalność dielektryczna środowiska, oraz
mniejsza jego lepkość (mikrolepkość).
Intensywność fluorescencji
Na intensywność fluorescencji mają wpływ dwa podstawowe czynniki:
liczba cząsteczek w stanie wzbudzonym zależna od długości fali światła wzbudzającego
wydajność kwantowa fluorescencji związana ze względnym prawdopodobieństwem przejść
promienistych i bezpromienistych
Dużą liczbę cząsteczek w stanie wzbudzonym można uzyskać stosując światło wzbudzające
odpowiadające maksimum absorpcji. Wydajność kwantowa zależy przede wszystkim od
prawdopodobieństwa przejść bezpromienistych. Można ją w pewnym stopniu regulować dobierając
odpowiednie warunki pomiaru.Przejścia energetyczne związane z fluorescencją szczególnie wygodnie
jest śledzić na tzw. diagramie Jabłońskiego (rysunek poniżej). Występują na nim trzy stany
elektronowe: singletowy stan podstawowy, S0, singletowy stan wzbudzony, S1, oraz wzbudzony stan
tripletowy, T1. Strzałki ciągłe pokazują przejścia promieniste, a strzałki przerywane przejścia
bezpromieniste.
7
Część IV: Optyczne metody badania oddziaływań
S1
Absorpcja
Fluorescencja
T1
Fosforescencja
S0
Jedną
z
przyczyn
obniżenia
intensywności
fluorescencji
jest
bezpromieniste
wewnątrzcząsteczkowe przejście pomiędzy singletowym stanem wzbudzonym S1 i singletowym
stanem podstawowym S0. W procesie tym energia stanu wzbudzonego jest rozpraszana na skutek
zderzeń z cząsteczkami rozpuszczalnika i/lub na skutek wewnątrzcząsteczkowego wzbudzania
oscylacyjnego innych fragmentów cząsteczki.
Prawdopodobieństwo występowania tego przejścia silnie zależy od temperatury układu. Zależność ta
komplikuje zastosowanie pomiarów fluorescencyjnych do obserwacji zmian konformacyjnych
biopolimerów wywołanych zmianami temperatury.
Wygaszanie fluorescencji
Zanik stanu wzbudzonego może również zachodzić na skutek zderzeń lub tworzenia
kompleksów z obecnymi w roztworze cząsteczkami zdolnymi do wygaszania fluorescencji. Zjawisko
to można wykryć wykonując pomiary wydajności kwantowej przy różnych stężeniach wygaszacza.
Bardzo wydajnymi wygaszaczami są: gazowy tlen O2 lub jony jodkowe J-. Wygaszacze te są w stanie
zneutralizować stan wzbudzony przy pojedynczym zderzeniu. Szybkość ich działania ograniczona jest
jedynie szybkością dyfuzji.
Fosforescencja
Kolejną przyczyną spadku intensywności fluorescencji jest przejście z singletowego stanu
wzbudzonego S1 do trypletowego stanu wzbudzonego T1 (patrz diagram Jabłońskiego). Jest to
przejście formalnie wzbronione. Występuje jednak z niezerowym prawdopodobieństwem w niektórych
układach molekularnych. Stan trypletowy T1 jest względnie trwały, gdyż przejście promieniste do
stanu podstawowego S0 jest wzbronione. Zachodzi jednak z niezerowym prawdopodobieństwem dając
zjawisko fosforescencji. Cząsteczki mogą pozostawać w stanie trypletowym przez godziny a nawet
dni, wiec fosforescencję można obserwować długo po ustaniu naświetlania wzbudzającego.
8
Część IV: Optyczne metody badania oddziaływań
4.2 Aktywność optyczna
W fali elektromagnetycznej wzajemnie prostopadłe wektory pola elektrycznego, E (niebieski
na rysunku poniżej), i indukcji magnetycznej, B (czerwony), zmieniają sinusoidalnie swoją długość.
Faza zmian pola magnetycznego przesunięta jest o 90° względem zmian pola elektrycznego.
E
B
Za oddziaływanie promieniowania elektromagnetycznego z materią odpowiada oscylacja pole
elektrycznego. Wektor tego pola jest zawsze prostopadły do kierunku rozchodzenia się fali.
Źródła światła generują fale o przypadkowych kierunkach drgań wektora pola
elektrycznego. Światło takie nazywamy światłem niespolaryzowanym (niezorientowanym).
4.2.1 Światło spolaryzowane
W specjalnych warunkach można uzyskać światło w którym wszystkie fale posiadają
jednakową płaszczyznę drgań pola elektrycznego. Światło takie nazywamy światłem spolaryzowanym
liniowo, a wspólną płaszczyznę drgań pola elektrycznego płaszczyzną polaryzacji. Światło
spolaryzowane uzyskać można np. w efekcie odbicia niskokątowego:
Układ optyczny zdolny do przepuszczania jedynie światła spolaryzowanego liniowo w pewnej
wyróżnionej płaszczyźnie nazywamy polaryzatorem.
Układ
dwóch
skrzyżowanych
polaryzatorów nie przepuszcza światła:
9
Część IV: Optyczne metody badania oddziaływań
Roztwory niektórych substancji posiadają zdolność do skręcania płaszczyzny polaryzacji.
Umieszczenie takiego roztworu pomiędzy skrzyżowanymi polaryzatorami powoduje, że za drugim
polaryzatorem pojawia się promień o niezerowym natężeniu:
Miarą aktywności optycznej próbki jest kąt φ o jaki zmienia się położenie płaszczyzny polaryzacji.
Zjawisko to nosi nazwę skręcalności optycznej.
φ
Polaryzacja eliptyczna
Wektor pola elektrycznego fali po przejściu przez aktywną optycznie próbkę nie oscyluje w
płaszczyźnie. Przemieszcza się po elipsie, której oś długa skręcona jest o kąt φ względem płaszczyzny
polaryzacji światła padającego. Światło takie nazywamy spolaryzowanym eliptycznie:
y
y
φ
1
1
2
2
3
3
x
x
4
4
5
5
Światło padające
Światło przechodzące
(polaryzacja liniowa)
(polaryzacja eliptyczna)
Miarą eliptyczności, θ, jest arkus tangens stosunku osi krótkiej i długiej elipsy zakreślanej przez
wektor pola elektrycznego. Np. gdy stosunek osi krótkiej do długiej wynosi 1/100 eliptyczność, θ,
równa jest 0,57 stopnia.
Dichroizm kołowy
Przy opisie polaryzacji eliptycznej wygodnie jest posłużyć się pojęciem światła
spolaryzowanego kołowo. W fali spolaryzowanej kołowo koniec wektora pola elektrycznego porusza
10
Część IV: Optyczne metody badania oddziaływań
się po linii śrubowej. Mogą istnieć dwa rodzaje światła spolaryzowanego kołowo: prawoskretne i
lewoskretne. Światło spolaryzowane liniowo można traktować jako superpozycję dwóch fal: jednej
spolaryzowanej kołowo w lewo, EL, i drugiej spolaryzowanej kołowo w prawo, ER.
y
y
y
1
1
1
3
x
2
2
2
+
3
4
x
=
3
4
4
5
5
EL
ER
x
5
W środowisku aktywnym optycznie absorbancja fali spolaryzowanej kołowo w lewo, AL, i
absorbancja fali spolaryzowanej kołowo w prawo, AR, jest różna.Zjawisko to nosi nazwę dichroizmu
kołowego (CD, ang. Circular Dichroism).
Po opuszczeniu próbki obydwie fale są dalej spolaryzowane kołowo różnią się jednak intensywnością
(promieniem linii śrubowej). Superpozycja tych fal daje w efekcie światło spolaryzowane eliptycznie:
y
y
φ
y
1
1
1
2
3
4
5
x
+
2
2
3
x
3
=
4
4
5
x
5
Miarą dichroizmu kołowego jest eliptyczność θ.
Różnica w absorpcji fali spolaryzowanej kołowo w lewo i w prawo oznacza, że aktywna
optycznie próbka posiada różne współczynniki załamania światła dla fali spolaryzowanej kołowo w
lewo, nL, i w prawo, nR. Jedna z nich porusza się w próbce szybciej niż druga i po opuszczeniu próbki
różnią się one fazą oscylacji. Przejawia się to występowaniem skręcalności optycznej, φ.
Podstawowe zależności
Można wykazać, że pomiędzy opisanymi wielkościami zachodzą relacje:
φ = 180L(n L − n R ) / λ
θ = 2,303(A L − A R )180 / 4π
Różnice we współczynnikach załamania są zwykle bardzo małe, dlatego korzystniej jest mierzyć
skręcalność optyczną bezpośrednio jako kąt φ. Dla typowych roztworów biopolimerów o stężeniu
11
Część IV: Optyczne metody badania oddziaływań
-4
chromoforu ok. 10 M i drodze optycznej L = 1 cm kąt skręcenia φ wynosi od 0,01 do 0,001 stopnia.
Współczesne sterowane komputerem przyrządy są w stanie zmierzyć skręcalność na poziomie
-5
10 stopnia.
Eliptyczność, θ, światła opuszczającego próbkę jest zwykle bardzo mała i trudna do precyzyjnego
pomiaru. Dlatego dichroizm kołowy najłatwiej jest zmierzyć przepuszczając naprzemiennie przez
próbkę wiązki spolaryzowane kołowo w lewo i w prawo i mierząc różnicę w natężeniu obu wiązek.
Różnica ta, ΔA, wynosi zwykle od 0,03% do 0,3% ogólnej absorbancji. Jest to wielkość łatwo
mierzalna przez współczesne aparaty.
4.2.2 Widma aktywności optycznej
Skręcalność optyczna próbki, φ, i jej zdolność do indukowania eliptyczności, θ, silnie zależą od
długości fali i mają największe natężenie w obszarze pasma absorpcji. Zależność φ(λ) nazywamy
dyspersją skręcalności optycznej lub widmem ORD (ang. Optical Rotatory Dispersion), a zależność
θ(λ) widmem dichroizmu kołowego lub widmem CD.
Widmo absorpcyjne
200
220
240
260
280
300
Widmo ORD
Widmo CD
200
200
220
240
260
280
220
240
260
280
300
300
Widmo CD
Dla przejście dozwolonego (np. π→π*) kształt widma
Widmo absorpcyjne
CD jest bardzo zbliżony do kształtu widma absorpcji (tzw. efekt
Cottona). Dzieje się tak dlatego, że w zakresie pasma absorpcji
ΔA
jest
zwykle
proporcjonalne
do
A.
Poza
pasmem
200
220
240
260
280
300
absorpcyjnym AL ≈ 0 i AR ≈ 0, więc ich różnica proporcjonalna do eliptyczność θ też jest bliska 0.
Efekt Cottona może mieć znak dodatni lub ujemny w zależności
Widmo CD
od asymetrii występującej w otoczeniu chromoforu. Natężenie
+
200
220
240
260
280
300
12
Część IV: Optyczne metody badania oddziaływań
efektu Cottona silnie zależy nawet od niewielkich zmian w strukturze i otoczeniu chromoforu.
Widmo ORD
Widmo ORD
Kształt widm ORD przypomina przebieg pierwszej
pochodnej
widma
absorpcyjnego.
Podstawowa
+
różnica
występuje poza pasmem absorpcji: skręcalność optyczna, φ, ma
200
220
240
260
280
300
niezerową wartość nawet daleko poza pasmem absorpcji. Na
krzywych ORD znak efektu Cottona przejawia się kolejnością skręcalności dodatniej i ujemnej.
Widma ORD stosuje się w zasadzie jedynie do cząsteczek o
pojedynczym
chromoforze.
Przy
większej
Widmo ORD - dwa izolowane chromofory
liczbie
chromoforów, nawet o oddzielnych pasmach absorpcji,
krzywe ORD poszczególnych chromoforów nakładają się
200
220
240
260
280
300
320
praktycznie uniemożliwiając analizę widma.
Pasma efektu Cottona w widmach CD są węższe a same widma łatwiejsze do analizy.
4.3 Polaryzacja fluorescencji
Procesom absorpcji i emisji promieniowania elektromagnetycznego przez cząsteczki
towarzyszy zmiana momentu dipolowego. Momenty dipolowe stanu podstawowego i wzbudzonego
leżą zwykle w tej samej płaszczyźnie, lecz mają różne kierunki:
M*
M
Stan podstawowy
Stan wzbudzony
Jeżeli oświetlimy próbkę światłem spolaryzowanym liniowo, to pochłaniać światło będą przede
wszystkim te cząsteczki, których momenty dipolowe są równoległe do kierunku drgań wektora pola
elektrycznego. Gdy absorbujące cząsteczki są unieruchomione, to fluorescencja jest również
spolaryzowana i to w kierunku równoległym do kierunku polaryzacji światła wzbudzającego.
Mierząc natężenie fluorescencji po przejściu przez polaryzator zorientowany:
I||
równolegle
I⊥
i prostopadle
13
Część IV: Optyczne metody badania oddziaływań
do płaszczyzny polaryzacji światła wzbudzającego otrzymujemy dwie wartości natężenia
fluorescencji: I|| oraz I⊥. Miarą polaryzacji fluorescencji może być:
stopień polaryzacji, P, definiowany wzorem:
P=
anizotropia fluorescencji, r, obliczana jako:
r=
I || − I ⊥
I || + I ⊥
lub
I || − I ⊥
I || + 2 I ⊥
4.4 Dichroizm liniowy (LD)
Dichroizm liniowy, LD (ang. Linear Dichroism) jest techniką spektroskopową używaną przede
wszystkim do badania struktury i orientacji chromoforów w cząsteczkach. Zjawisko dichroizmu
liniowego związane jest z różną absorpcją światła spolaryzowanego równolegle i prostopadle w
stosunku do wybranej osi cząsteczki. Wyniki pomiarów rejestrowane są w formie widma LD, czyli
zależności natężenia zjawiska od długości fali.
Obecnie największe zastosowanie znajduje technika LD przy badaniu biopolimerów (DNA, białka)
oraz polimerów syntetycznych. Niektóre wersje tej techniki pozwalają również na badanie
małocząsteczkowych związków organicznych oraz kryształów.
4.4.1 Podstawy teoretyczne
Gdy wiązka światła pada na cząsteczkę część z niej ulega absorpcji.
Ilość zaabsorbowanego światła zależy przede wszystkim od długości fali, λ.
Na przykład chlorofil absorbuje światło głównie przy długości fali ok.
430 nm (niebieskie) i 670 nm (czerwone). Ponadto w widmie absorpcyjnym
chlorofilu występuje jeszcze kilka dużo słabszych pasm absorpcji.
Absorpcja promieniowania elektromagnetycznego z zakresu widzialnego i
bliskiego nadfioletu związana jest ze wzbudzeniem elektronowym, czyli
przejściem elektronu na wyższy poziom energetyczny.
Wielkością
która
determinuje
prawdopodobieństwo wzbudzenia
r
elektronu jest dipolowy moment przejścia μ if . Jest to wektor, którego
r
E
θ
r
μ if
przestrzenna orientacja jest dla danego rodzaju chromoforu i typu
wzbudzenia (σ→σ*, n→π*, π→π*) jednoznacznie zdefiniowana.
Wzbudzenie elektronowe zmienia przestrzenny rozkład gęstości elektronowej w cząsteczce i
wywoływane jest przez składową elektryczną fali elektromagnetycznej. Zależność pomiędzy
r
wydajnością wzbudzenia a wektorem pola elektrycznego fali elektromagnetycznej, E , i wektorem
r
momentu przejścia, μ if , dana jest zależnością:
(
r r
dN i
∝ μ if ⋅ E
dt
)2 = μif2 E 2 cos 2 (θ)f (λ )
14
Część IV: Optyczne metody badania oddziaływań
gdzie: f(λ) definiuje kształt pasma absorpcji.
Z zależności tej wynika jednoznacznie, że wydajność wzbudzenia, a więc i absorbancja próbki zależy
nie tylko od wielkości dipolowego momentu przejścia, ale również od jego orientacji względem
wektora pola elektrycznego: kąta θ. Dlatego w pomiarach dichroizmu liniowego stosuje się światło
spolaryzowane liniowo, czyli promieniowanie elektromagnetyczne, którego wektor pola elektrycznego
drga tylko w jednej płaszczyźnie.
Dipolowy moment przejścia posiada jednoznacznie zdefiniowaną orientację względem
chromoforu. Orientację tę można wyznaczyć dwoma sposobami:
-
obliczeniowym: orientację momentu przejścia można obliczyć jeżeli znana jest funkcja
falowa cząsteczki w stanie podstawowym i wzbudzonym
-
doświadczalnie z pomiarów absorpcji światła spolaryzowanego przez monokryształ badanej
substancji
Na przykład dwa główne momenty przejścia w cząsteczce chlorofilu a związane są ze wzbudzeniem
układu porfirynowego. Oba wektory momentów przejścia leżą w
670 nm
płaszczyźnie układu porfirynowego, lecz są do siebie prostopadłe
(rysunek na poprzedniej stronie). Można więc korzystając ze
światła spolaryzowanego liniowo określić jak cząsteczka
chlorofilu związana z określonym białkiem lub kompleksem
430nm
białek ustawiona jest w przestrzeni. Należy w tym celu dokonać
pomiaru absorpcji światła spolaryzowanego liniowo w dwóch
wzajemnie prostopadłych kierunkach. Technika spektroskopowa
oparta na takich pomiarach nosi nazwę dichroizmu liniowego,
LD.
Podstawowym ograniczeniem techniki LD jest konieczność
zapewnienia
jednakowej
orientacji
cząsteczek
w
skali
makroskopowej całej próbki. Cząsteczki w roztworach oraz w
większości
ciał
stałych
mają
w
skali
makroskopowej
przypadkową orientację i dlatego w takich środowiskach
dichroizm liniowy jest niemierzalny. Wyjątkiem od tej zasady są
monokryształy oraz zorientowane struktury supramolekularne. Zwłaszcza te ostatnie wykorzystywane
są powszechnie w badaniach biofizycznych.
Wyobraźmy
sobie,
że
udało
nam
się
uzyskać
E||
makroskopową próbkę liniowego dwuniciowego DNA w
której osie wszystkich heliks ustawione są w pewnym
wyróżnionym kierunku. Wektory momentów przejścia
E0||
E⊥
15
E0⊥
Część IV: Optyczne metody badania oddziaływań
zasad występujących w DNA leżą w płaszczyźnie tych zasad, a więc w przypadku helisy B
prostopadle do osi tej helisy. Dokonujemy teraz pomiaru absorpcji światła spolaryzowanego liniowo
równolegle do osi helisy i prostopadle do niej. Wiązka światła spolaryzowana równolegle do osi helisy
(prostopadle do płaszczyzny zasad i wektorów momentów przejścia) powinna przejść przez próbkę
praktycznie niezmieniona podczas gdy wiązka o polaryzacji prostopadłej do osi helisy (równoległej do
wektorów przejścia) powinna zostać w znacznym stopniu zaabsorbowana.
Miernik dichroizmu
Absorbancja wiązki światła poruszającej się wzdłuż osi Oy i spolaryzowanej zgodnie z osią Ox
dana jest wzorem:
A x = kμ 2 cos 2 θ x
gdzie:
cos 2 θ x oznacza wartość uśrednioną po wszystkich cząsteczkach znajdujących się w wiązce
światła
Jeżeli w badanej próbce nie występuje żaden rodzaj uporządkowania chromoforów (próbka jest
izotropowa) to:
cos 2 θ x = cos 2 θ y = cos 2 θz = 1
3
Tym samym:
1
A x = A y = A z = kμ 2 = A izo
3
gdzie: Aizo – absorbancja niespolaryzowanego światła przez izotropową próbkę
Dla wiązki poruszającej się wzdłuż osi Oy najprostszym miernikiem dichroizmu liniowego jest
wielkość:
ΔA = A z − A x
Wadą tego miernika jest jego zależność od stężenia próbki. Dlatego wprowadzono bezwymiarowy
miernik zwany zredukowanym dichroizmem liniowym, LDr:
LDr =
Az − Ax
= cos 2 θz − cos 2 θ x
3A izo
Dla próbki izotropowej wartość tego miernika wynosi:
LDr =
1 1
− = 0,
3 3
a dla próbki w której wektory momentów przejścia są idealnie zorientowane wzdłuż osi Oz wynosi:
LDr = 1 − 0 = 1 .
Istnieją dwie przyczyny dla których zmierzona wartość zredukowanego dichroizmu liniowego
może być mniejsza od 1:
16
Część IV: Optyczne metody badania oddziaływań
częściowa a nie idealna orientacja cząsteczek w próbce,
wektor momentu przejścia nie pokrywa się z kierunkiem orientacji cząsteczek.
W badanej próbce przyczyny te mogą występować oddzielnie lub łącznie. Zwykle orientację wektora
momentu przejścia w stosunku do kierunku orientacji cząsteczki można oszacować z innych
pomiarów. Niewiadomą pozostaje jednak stopień uporządkowania cząsteczek w próbce.
θ μ12
Wektor momentu przejścia nie pokrywa się z kierunkiem orientacji cząsteczki
Rozważmy sytuację, gdy cząsteczki o kształcie pręta są idealnie μ12 θ
zorientowane zgodnie z osią Oz (rysunek obok) i zawierają tylko jeden
chromofor zdolny do absorpcji światła w badanym zakresie długości fali.
Załóżmy ponadto, że pomiędzy kierunkiem wektora momentu przejścia, μ12, a
kierunkiem orientacji występuje niezerowy kąt θ. Spróbujmy przewidzieć jaka będzie w tym
przypadku wartość LDr.
Przede wszystkim musimy zwrócić uwagę, że orientacja cząsteczek zgodnie z osią Oz definiuje
jednoznacznie wartość kąta θ, ale nie określa wartości kąta ϕ. Absorbancję światła spolaryzowanego
zgodnie z kierunkiem osi Oz, Az, można więc łatwo zdefiniować wzorem:
2
A z = kμ12
cos 2 θ .
Wyznaczenie absorbancji światła spolaryzowanego zgodnie z kierunkiem
z
Ox wymaga jednak bardziej skomplikowanych obliczeń:
2
A x = kμ12
θ
2π
1 2
2
2
2
∫ sin θ cos ϕdϕ = 2 kμ12 sin θ .
0
ϕ
Teraz możemy wyznaczyć wartość zredukowanego dichroizmu liniowego:
1
cos θ − sin 2 θ
A − Ax
1
2
=
LDr = z
= 3 cos 2 θ − 1
2
2
3A izo
2
cos θ + sin θ
2
(
μ12
x
y
)
Z uzyskanej zależności wynika, że istnieje taki kąt θM przy którym wartość zredukowanego
dichroizmu równa jest zero pomimo idealnej orientacji wszystkich cząsteczek. Ten tzw. kąt magiczny
występuje, gdy cos2θ = 1/3 i wynosi θM = 54,7°.
4.4.2 Orientacja cząsteczek w próbce
Zjawisko dichroizmu liniowego zostało początkowo stwierdzone w przypadku niektórych
kryształów. Po wyjaśnieniu jego podłoża fizycznego stało się jasne, że technika ta może być
wykorzystana również do badania biopolimerów. Zjawisko dichroizmu liniowego zaobserwowano
początkowo tylko w układach biologicznych o uporządkowaniu dalekozasięgowym. Uporządkowanie
takie występuje np. we włóknach mięśniowych.
17
Część IV: Optyczne metody badania oddziaływań
W latach ’60 XX w. opracowano metody wymuszonej orientacji cząsteczek organicznych.
Mogą być one stosowana w przypadku cząsteczek o wydłużonym kształcie. Ich efektywność wzrasta
jeżeli wektor momentu przejścia rozpatrywanego chromoforu pokrywa się z osią długą cząsteczki lub
jest do niej prostopadły.
Zaproponowano szereg metod orientacji cząsteczek w próbce. W chwili obecnej najczęściej
stosowane są:
rozciąganie folii polimerowych
orientacja hydrodynamiczna
równoległe biwarstwy lipidowe
Rozciągane folie polimerowe
W tej technice dla uzyskania orientacji wymuszonej wykorzystuje się efekt orientujący
rozciąganych łańcuchów polimerowych. Badaną substancję rozpuszcza się w roztworze polarnego
polimeru np. alkoholu poliwinylowego i wylewa do płytkiej wydłużonej rynienki.. Po odparowaniu
rozpuszczalnika ( w badaniach biofizycznych wody) pozostaje prostokątna kształtka polimeru z
równomiernie lecz chaotycznie rozmieszczonymi cząsteczkami badanej substancji (lewy panel na
rysunku poniżej).
Przed
rozciągnięciem
Po rozciągnięciem
Poddając kształtkę naprężeniu rozciągającemu doprowadzamy do plastycznego (trwałego) jej
odkształcenia. Kształtki z alkoholu poliwinylowego można rozciągnąć zwiększając ich wymiar nawet
o 50%. Podczas takiego rozciągania łańcuchy polimeru prostują się, układają równolegle i
przemieszczają się względem siebie ruchem ślizgowym. W tak silnie zorientowanym środowisku
cząsteczki badanej substancji również ulegają orientacji równolegle do kierunku działania sił
rozciągających (prawy panel). Uporządkowanie jest tym silniejsze im bardziej wydłużony kształt
posiada cząsteczka.
Rozciągniętą folię umieszcza się następnie prostopadle do kierunku wiązki światła
spolaryzowanego i wykonuje dwa pomiary lub widma. Podczas pierwszego pomiaru płaszczyzna
polaryzacji światła jest równoległa do kierunku orientacji wymuszonej, a podczas drugiego
prostopadła do tego kierunku.
Orientacja hydrodynamiczna
Obecnie najpowszechniej stosowaną techniką orientacji próbek ciekłych jest technika
hydrodynamiczna wykorzystująca tzw. przepływ Couette’a. Badaną próbkę umieszcza się w wąskiej
18
Część IV: Optyczne metody badania oddziaływań
przestrzeni pomiędzy obracającym się cylindrycznym naczyniem a nieruchomym, osiowo ustawionym
prętem (lewy panel rysunku poniżej).
Przy odpowiednio dobranej prędkości kątowej warstewka cieczy zaczyna się poruszać ruchem
laminarnym (efekt Couette’a). Ten laminarny przepływ cieczy wywołuje silny efekt orientujący na
cząsteczki obecne w roztworze (panel prawy). Efekt ten można dodatkowo zwiększyć używając
roztworów o dużej lepkości.
Równoległe biwarstwy lipidowe
Do ustalenia orientacji badanych cząsteczek w próbce można
również wykorzystać płaskie biwarstwy lipidowe. Na płytce kwarcowej
Z
wytwarza się układ kilkudziesięciu lub nawet więcej biwarstw lipidowych
ω
rozdzielonych warstewkami roztworu wodnego (rysunek obok). Układ taki
uzyskać można przez łagodne odwodnienie zawiesiny pęcherzyków
lipidowych, np. w strumieniu azotu.
B
ω
A
Płytkę kwarcową umieszcza się w przyrządzie pomiarowym w taki sposób, aby możliwy był obrót
płytki. Płytkę oświetla się od dołu wiązką światła (A) spolaryzowanego poziomo (kierunek polaryzacji
pokazuje strzałka B). Kąt ω definiuje położenie normalnej do powierzchni biwarstwy (Z) względem
kierunku płaszczyzny polaryzacji światła (B). Wykonując pomiary przy różnych wartościach kąta ω
określić można kąt φ pomiędzy normalną Z i wektorem momentu przejścia μ12.
4.5 Metody optyczne w badaniu oddziaływań
W wyniku powstawania kompleksów ligand-biopolimer zmianie ulega charakterystyka
spektralna chromoforu. Zmiana ta może być wynikiem:zmiany lokalnego otoczenia chromoforu
wystąpienia lub zaniku oddziaływań chromofor – chromofor
zmiany orientacji momentu dipolowego lub momentu przejścia
indukowanej asymetrii chromoforu
Tym samym chromofor można traktować jaku czułą sondę wrażliwą na zmiany wywołane
wystąpieniem oddziaływania. Jest to powodem szerokiego wykorzystania metod optycznych do
badania oddziaływania ligand-biopolimer.
19
Część IV: Optyczne metody badania oddziaływań
4.5.1 Zmiany lokalnego otoczenia chromoforu
W białkach i kwasach nukleinowych występują ugrupowania chemiczne mogące pełnić rolę
wewnątrzcząsteczkowych chromoforów. Są nimi np. układy aromatyczne takich aminokwasów jak
fenyloalanina, tyrozyna i tryptofan. Można je wykorzystać do śledzenia lokalnych lub globalnych
zmian konformacyjnych. Podejście to bywa wykorzystywane do:
badania wpływu środowiska (temperatura, siła jonowa itp.)
wykrywania powstawania IV-rzędowej struktury białek
określania zmian konformacyjnych indukowanych małocząsteczkowym ligandem (substratem,
modulatorem)
badania zmian konformacyjnych wywołanych modyfikacjami chemicznymi białek, np.
fosforylacją
ustalenia lokalizacji domen białkowych w środowiskach o różnej polarności, np. w błonach
biologicznych.
Podstawową wadą tego podejścia jest jego niska czułość. Naturalne chromofory maja zwykle niskie
ekstynkcje molowe i ich zawartość w biopolimerze też jest zwykle niewielka.
Dużo lepsze wyniki uzyskuje się, gdy chromofor jest ulokowany w ligandzie oddziałującym z
biopolimerem. Można wtedy tak dobrać chromofor, aby uzyskać dużą czułość pomiaru. W wyniku
oddziaływania z biopolimerem zmienia się lokalne otoczenie chromoforu, a tym samym również jego
widmo absorpcyjne i fluorescencyjne.
W przypadku widm absorpcyjnych zmiana lokalnego otoczenia wpływa na:
przesuniecie maksimum absorpcji
zmianę ekstynkcji molowej
zmianę kształtu widma (zmiana względnej intensywności pasm oscylacyjnych)
W przypadku widm fluorescencyjnych zmiany dotyczą:
zmian intensywności fluorescencji (nawet o kilka rzędów wielkości)
zmiany położenia pasma – zmiany barwy emitowanego światła.
Właściwie dobrany chromofor lub fluorochrom pozwala uzyskać bardzo dużą czułość i selektywność
pomiarów. Dotyczy to w szczególności ligandów fluorescencyjnych.
4.5.2 Oddziaływania chromofor-chromofor
Przy bliskim kontakcie 2 chromoforów powstaje nowa funkcja falowa i nowe poziomy
energetyczne. Zmianie ulega położenie i intensywność pasm absorpcyjnych. Wielkość tych zmian
zależy od:odległości chromoforów
kąta pomiędzy momentami przejścia
poziomów energetycznych niezaburzonych chromoforów
20
Część IV: Optyczne metody badania oddziaływań
Znając momenty przejścia niezaburzonych chromoforów można ustalić relacje geometryczne
pomiędzy badanymi chromoforami. Efekty te są najsilniejsza gdy chromofory absorbują w podobnym
zakresie długości fali. Szczególnie silne są wtedy, gdy oddziałują ze sobą takie same chromofory, np.
podczas tworzenia dimerów.
W przypadku gdy jeden z chromoforów jest jednocześnie fluorochromem pojawiają się
dodatkowe efekty: tłumienie fluorescencji (ang. quenching) oraz transfer energii.
Tłumienie fluorescencji
Podstawą zjawiska tłumienia fluorescencji jest oddziaływanie wzbudzonego fluorochromu ze
znajdującym się w jego bezpośredniej bliskości chromoforem. Oddziaływanie to ułatwia
bezpromieniste przejście fluorochromu do podstawowego stanu elektronowego, a tym samym
obniżenie intensywności fluorescencji. Należy z całą mocą podkreślić, że zjawisko to nie polega na
następującej po sobie emisji i absorpcji kwantu światła, lecz ma naturę kwantowo-chemiczną.
Zachodzi wtedy, gdy funkcje falowe obu układów zachodzą na siebie w przestrzeni.
Tłumienie fluorescencji występuje również pomiędzy dwoma fluorochromami – takimi samymi lub
różnymi. Jeden z nich pełni wtedy rolę chromoforu. Tłumienie fluorescencji wyjaśnia znany od wielu
lat fakt, że dimery znaczników fluorescencyjnych wykazują fluorescencję o kilka rzędów wielkości
słabszą niż znaczniki w rozproszeniu monomerycznym.
Metoda wypierania znacznika
Na opisanym powyżej zjawisku opiera się jedna z metod wyznaczania stałej wiązania ligandów
przez biopolimer. Wykorzystuje się w niej znacznik fluorescencyjny wiążący się z biopolimerem jako
monomer i wykazujący w tym stanie bardzo silną fluorescencję. Znacznik musi jednocześnie ulegać
silnej agregacji w roztworze wodnym, a jego agregaty muszą wykazywać, w efekcie tłumienia, bardzo
słabą fluorescencję. Jeżeli do roztworu dodamy teraz lidand wiążący się kompetytywnie do tego
samego miejsca wiązania, to będzie on wypierał znacznik do roztworu, a w efekcie wystąpi spadek
fluorescencji. Miareczkując kompleks biopolimer-znacznik ligandem możemy wyznaczyć takie
stężenie liganda, c50, przy którym intensywność fluorescencji zmniejsza się do połowy wartości
początkowej.
Znając stałą wiązania znacznika oraz jego stężenie oraz wartość c50 możemy łatwo wyznaczyć stałą
wiązania liganda. Technika ta jest np. powszechnie stosowana do wyznaczania stałych interkalacji
różnych związków do dwuniciowego DNA. Jako znacznika fluorescencyjnego używa się zwykle
bromku etydyny.
Transfer energii
Bliskie sąsiedztwo przestrzenne 2 różnych fluorochromów może prowadzić do przeniesienia
wzbudzenia z jednego z nich na drugi. Zjawisko to nosi nazwę transferu energii i można je
przedstawić jako wypadkową trzech kolejno następujących po sobie procesów:
21
Część IV: Optyczne metody badania oddziaływań
D + hν1 = D*
wzbudzenie donora
D* + A = D + A*
transfer energii – przeniesienie wzbudzenia na akceptor
A* = A + hν2
fluorescencja akceptora
Warunkiem wystąpienia transferu energii jest zachodzenie na siebie widma emisyjnego donora i
widma absorpcyjnego akceptora oraz bliskość przestrzenna i odpowiednia orientacja obu
fluorochromów. Analogicznie jak w przypadku tłumienia fluorescencji zjawisko to ma naturę
kwantowo-chemiczną.
Ponieważ podczas transferu energii część energii stanu wzbudzonego donora ulega
rozproszeniu, więc jako akceptor należy wybierać związek fluoryzujący przy większej długości fali niż
donor. Dla jednoznacznej interpretacji uzyskiwanych wyników długość fali światła wzbudzającego, ν1,
musi być tak dobrana, aby nie wywoływała wzbudzenia akceptora. Przy stosowaniu partnerów
spełniających powyższe reguły transfer energii przejawi się jako fluorescencja pochodząca od
znacznika który nie mógł być wzbudzony wiązką oświetlajacą.
Zjawisko transferu energii wykorzystuje się w pomiarach biofizycznych chcąc wykazać
możliwość występowania bliskich kontaktów pomiędzy donorem i akceptorem. Jeden z partnerów
może być np. kowalencyjnie związany z biopolimerem. Wystąpienie transferu energii świadczy wtedy,
że drugi partner ma powinowactwo do tego samego centrum aktywnego.
Innym zastosowaniem transferu energii może być badanie wnikania do błony lipidowej lub
penetracji przez nią. Przy badaniu wnikania jeden z partnerów znajduje się w biwarstwie lipidowej, a
drugi w roztworze wodnym. Wystąpienie transferu energii oznacza, że obaj partnerzy spotkali się
wewnątrz błony lipidowej.
Jeden z partnerów może być zamknięty wewnątrz pęcherzyków lipidowych (liposomów), a drugi
znajdować się w roztworze wodnym na zewnątrz pęcherzyków. Penetracja jednego lub obu partnerów
przez błonę pęcherzyka przejawi się wystąpieniem transferu energii.
4.5.3 Anizotropia fluorescencji
Światło spolaryzowane liniowo preferencyjnie wzbudza cząsteczki, których moment przejścia
jest zorientowany równolegle do płaszczyzny polaryzacji. Jeżeli pomiędzy absorpcją i emisją nie
nastąpi rotacja cząsteczki, to I|| > I⊥, a anizotropia fluorescencji będzie miała wartość maksymalną:
r = 0,4. Jeżeli fluorochrom ma dużą swobodę rotacyjną, to pomiędzy absorpcją i emisją dojdzie do
przypadkowego ustawienia wektora momentu przejścia i anizotropia fluorescencji zaniknie:
r ≈ 0.Kinetyka rotacji fluorochromu zależy od mikrolepkości środowiska lub stopnia usztywnienia
struktury, do której przyłączona jest sonda fluorescencyjna. Znając czas życia stanu wzbudzonego (z
innych pomiarów) i anizotropię fluorescencji możemy oszacować względną sztywność różnych części
układu, np. błony lipidowej.
22
Część IV: Optyczne metody badania oddziaływań
4.5.4 Widma CD
Efekt Cottona występuje w obszarze pasma absorpcyjnego asymetrycznie zaburzonego
chromoforu. Zaburzenie symetrii chromoforu może wynikać z:
obecności centrum chiralnego w sąsiedztwie chromoforu
elementów asymetrii w strukturze biopolimeru, np. α-helisa w białku
elementów asymetrii w strukturze kompleksu, np. śrubowego ułożenia cząsteczek w agregacie
zmiany konformacji liganda pod wpływem oddziaływania asymetrycznych fragmentów
biopolimeru (asymetria indukowana).
Natężenie efektu Cottona jest tym większe im silniejsze jest zaburzenie.
Dublet ekscytoniczny
Bliskie sąsiedztwo przestrzenne asymetrycznych chromoforów prowadzi do wystąpienia w
widmie CD tzw. dubletu ekscytonicznego.
Widm o CD
Widm o CD
200
200
220
240
260
280
220
240
260
280
300
300
Izolowany chromofor
Chromofor zagregowany
Dublet ekscytoniczny powstaje na skutek:
rozszczepienia pasma absorpcyjnego, oraz
przeciwnego znaku efektu Cottona dla każdego z nich.
Znając moment przejścia izolowanego asymetrycznego chromoforu oraz kształt i intensywność
dubletu ekscytonicznego można odtworzyć geometrię układu chromoforów.
Asymetria indukowana
Achiralny
ligand
oddziałujący
z
silnie
asymetrycznym
biopolimerem
może
ulec
asymetrycznemu zaburzeniu. Zjawisko to nazywamy asymetrią indukowaną. Typowym przykładem
asymetrii indukowanej jest występowanie efektu Cottona w widmach polimetylenopiroli (wzór
poniżej) oddziałujących z małym rowkiem podwójnej helisy B DNA. Długa cząsteczka liganda
wpasowuje się w mały rowek przyjmując kształt linii śrubowej. Wywołuje to silne asymetryczne
zaburzenie chromoforów pirolowych tworzących szkielet cząsteczki.
4.5.5 Dichroizm liniowy
Gdy chromofory w próbce są zorientowane wzdłuż wybranego kierunku widmo absorpcyjne
mierzone zgodnie z kierunkiem orientacji jest różne od widma mierzonego prostopadle do tego
kierunku. Efekt ten nazywamy dichroizmem liniowym (LD, ang. linear dichroism), a różnicę tych
23
Część IV: Optyczne metody badania oddziaływań
widm widmem LD. Dichroizm liniowy występuje tylko w zakresie pasma absorpcji zorientowanego
chromoforu.
Warto zapamiętać, że dla wystąpienia dichroizmu liniowego (w odróżnieniu od dichroizmu kołowego)
nie jest niezbędne chiralne zaburzenie chromoforu. Potrzebna jest jedynie makroskopowa orientacja
momentów przejścia.Zjawisko dichroizmu liniowego zaobserwowano początkowo tylko w układach
(biologicznych lub krystalicznych) o samoistnym uporządkowaniu dalekozasięgowym. W układach
ożywionych uporządkowanie takie stwierdzamy np. we włóknach mięśniowych. Obecnie znamy
szereg metod wymuszania orientacji cząsteczek w próbkach. Stosuje się je przede wszystkim do
cząsteczek o wydłużonym kształcie. Efektywność tych metod wzrasta dodatkowo, jeżeli wektor
momentu przejścia rozpatrywanego chromoforu pokrywa się z osią długą cząsteczki lub jest do niej
prostopadły.
DNA
Podwójna helisa DNA jest ze względu na swój kształt i względnie dużą sztywność niemal
idealnym obiektem badań z wykorzystaniem techniki LD. Dichroizm liniowy wykorzystany być może
do uzyskania informacji o:
1. lokalnych zmianach orientacji zasad w stosunku do osi długiej helisy
2. orientacji ligandu oddziałującego z DNA
W pierwszym przypadku korzysta się z pasm absorpcji zasad wchodzących w skład DNA, a w drugim
przypadku z możliwie długofalowych pasm absorpcyjnych liganda.
Białka włókniste
Większość białek strukturalnych ma jeden z wymiarów dużo większy niż pozostałe dwa.
Można je więc badać techniką LD po zorientowaniu jedną z opisanych wcześniej metod. Dla takich
biopolimerów szczególnie przydatna jest metoda hydrodynamiczna.
Pewnym utrudnieniem przy badaniu białek techniką LD jest brak w czasteczce białka chromoforu
posiadającego pasma absorpcji w obszarze widzialnym lub bliskiego ultrafioletu. Najbardziej
długofalowe pasmo absorpcji pochodzi od wiązania peptydowego i występuje przy ok. 210 nm, czyli
na granicy tzw. próżniowego UV. W paśmie tym nakładają się na siebie 3 przejścia: dwa wzajemnie
ortogonalne przejścia π→π* oraz jedno przejście n→π*.
24
Część IV: Optyczne metody badania oddziaływań
π //
π⊥
π⊥
Orientacje odpowiadających im momentów przejścia zależą od: i) rodzaju struktury
II-rzędowej łańcucha peptydowego oraz ii) orientacji tej struktury względem osi długiej cząsteczki.
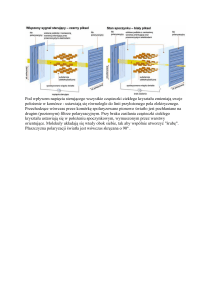
Elementem struktury II-rzędowej białek, szczególnie łatwym do
wykrycia w widmie LD jest helisa alfa. W widmie tej struktury
(rysunek obok) jedno z przejść π→π* jest prawie prostopadłe, a
drugie prawie równoległe do osi helisy. Przejściu n→π*
odpowiada zwykle bardzo słaby sygnał LD. W innych strukturach
II-rzędowych wzajemne proporcje sygnałów pochodzących od
poszczególnych przejść nie są tak charakterystyczne.
Na rysunku obok pokazano również widmo absorpcyjne
próbki w świetle niespolaryzowanym: szara linia i prawa skala. Na
uwagę zasługuje fakt, że dichroizm liniowy pochodzi od przejść,
które na widmie absorpcyjnym są trudne do wychwycenia.
Białka błonowe
W komórce bardzo wiele białek związanych jest z błona komórkową. Mogą to być białka
powierzchniowe (ułożone równolegle do powierzchni błony) lub białka transbłonowe (przebijające
błonę w przybliżeniu prostopadle do jej powierzchni). Do badania białek tego typu techniką LD
szczególnie przydatne okazały się równoległe biwarstwy lipidowe.
Do
badania
oddziaływania
biopolimerów
a
nawet
małocząsteczkowych
związków
organicznych z błona lipidową wykorzystać można również inny układ modelowy: duże
jednopowlokowe pęcherzyki lipidowe (LUV, ang. Large Unilamellar Vesicles). Efekt orientujący
uzyskuje się pośrednio dzięki zastosowaniu metody hydrodynamicznej. LUV są na tyle elastyczne, że
25
Część IV: Optyczne metody badania oddziaływań
przepływu cieczy wywołuje ich deformację: izotropowa forma sferyczna zmienia się w anizotropową
formę elipsoidalną (rys. A poniżej).
Tak zdeformowane pęcherzyki układają się ponadto swymi osiami długimi zgodnie z kierunkiem
przepływu cieczy.
Związki (biopolimery lub małocząsteczkowe ligandy) mogą oddziaływać z błoną na kilka różnych
sposobów (rys. B – E). Jeżeli oddziaływanie to prowadzi do orientacji cząsteczek w stosunku do
powierzchni błony (np. D – równolegle, E – prostopadle) to uzyskamy wyraźne i łatwe do interpretacji
widma LD.
26