Najbardziej realny jest przypadek występowania w półprzewodniku

Zjawiska kontaktowe i powierzchniowe w półprzewodnikach –W4
SMK
Na podstawie: „Przyrządy półprzewodnikowe i układy scalone”, W. Marciniak, WNT,
Warszawa 1987
Najbardziej realny jest przypadek występowania w półprzewodniku jednocześnie obu
rodzajów domieszek – donorowych i akceptorowych. Rodzaj przewodnictwa w
półprzewodniku określony jest tymi domieszkami, których koncentracja jest większa.
W określonym półprzewodniku w określonej temperaturze, iloczyn koncentracji
elektronów i dziur jest wielkością stałą, niezależną od rodzaju domieszkowania, równą ni2.
Półprzewodnik samoistny: ni = pi
Półprzewodnik typu n: n = (ND-NA) dla ND>NA
Półprzewodnik typu p: p = (NA-ND) dla NA>ND
Półprzewodnik skompensowany: NA=ND t.j. ni = pi (domieszkowanie krzemu złotem)
Stan równowagi półprzewodnika – pp ma ustaloną temperaturę i nie jest poddany
żadnym zewnętrznym oddziaływaniom energetycznym (pole elektryczne, jonizujące).
W przypadku elektronów w ciele stałym dodatkowe ograniczenie do rozkładu
energetycznego wprowadza zasada Pauliego, stąd statystyka i rozkład Fermiego-Diraca:
1
f n (W ) 
; f p (W )  1  f n (W );
1  exp(W  WF ) / kT

n
 N (W ) f n (W )dW ; p 
Wc
0
 N (W ) f
p
(W )dW
Wv
fn(W), fp(W) - funkcje rozkładu prawdopodobieństwa zajęcia poziomu o energii W przez
elektron i dziurę, N(W) – rozkład koncentracji poziomów energetycznych w funkcji energii.
WF – energia Fermiego – potencjał chemiczny, tzn. średnia energia swobodna elektronów
liczona na jeden elektron.
Efektywne koncentracje stanów energetycznych sprowadzonych do poziomów dna
pasma przewodnictwa (Nc) oraz wierzchołka pasma walencyjnego (Nv):
n  N c f n (Wc )  N c exp[(WF  Wc ) / kT ]; p  N v f p (Wv )  N v exp[(Wv  WF ) / kT ]
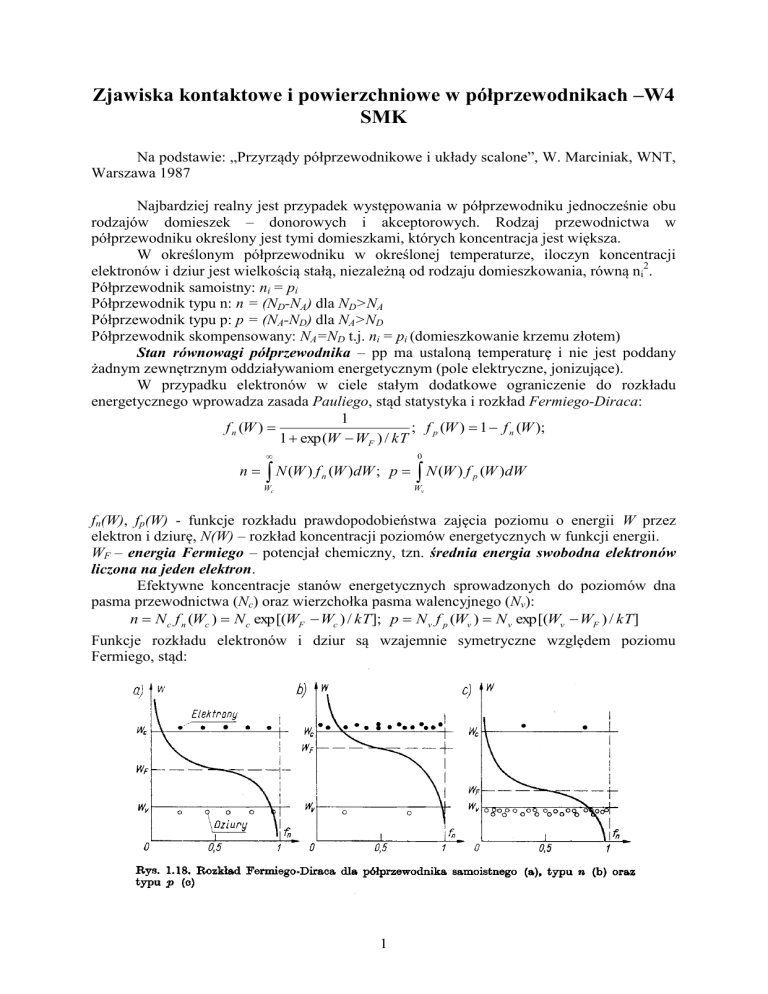
Funkcje rozkładu elektronów i dziur są wzajemnie symetryczne względem poziomu
Fermiego, stąd:
1
Koncentracja nośników w półprzewodniku samoistnym:
T
ni2  N c N v exp( Wg / kT ); ni  B( ) 3 / 2 exp( Wg / 2kT ); N c , N v  T 3 / 2
To
Zależności Boltzmanna:
n  ni exp(q F / kT ); p  ni exp(q F / kT );  F  (Wi  WF ) / q  potencjal Fermiego
Bilans koncentracji nośników:
np  ni2
Równanie neutralności elektrycznej – koncentracja ładunku elektrycznego utworzonego
przez elektrony, dziury, dodatnie jony domieszki donorowej i ujemne jony domieszki
akceptorowej jest równa zeru:
 = q(p-n+ND-NA)=0
Transport nośników w półprzewodniku – w prądzie przewodzenia, utworzonym przez
poruszające się nośniki, należy rozróżnić dwa mechanizmy: unoszenie i dyfuzję:
Jc=Ju+Jd
Unoszenie – strumień nośników poruszających się wskutek działania siły elektrycznej
Ju = qnvu = qnE
vu – średnia prędkość unoszenia w polu elektrycznym, vu=E,  – ruchliwość ładunków,
=qtzd/2mn*. Ruchliwość zależy od koncentracji domieszek, temperatury, natężenia pola
elektrycznego; tzd-średni czas między zderzeniami, mn*-masa efektywna elektronu.
Dyfuzja – składowa prądu dyfuzji występuje wówczas, gdy rozkład koncentracji
nośników prądu jest nierównomierny. W wyniku dyfuzji następuje proces wyrównywania ich
koncentracji. Gęstość prądu dyfuzji jest proporcjonalna do wartości gradientu koncentracji
nośników, a współczynnik proporcjonalności – współczynnik dyfuzji:
J dn  qDn gradn; J dp  qD p gradp
Istnieje ścisły związek pomiędzy ruchliwością a współczynnikiem dyfuzji – wzór Einsteina:
D
kT

q
J  J n  J p  q n nE  qDn gradn  q p pE  qD p gradp

W stanie równowagi termodynamicznej szybkość generacji nośników Go równa się szybkości
ich rekombinacji Ro (Go/Ro – liczba par elektron-dziura powstających/znikających w 1m3
objętości kryształu w czasie 1s).
G  Ro  r * nno * pno
Półprzewodnik w stanie nierównowagi termodynamicznej. Jeśli do pp nośniki są
dostarczone, n*p > ni2 – wstrzykiwanie (injekcja) nośników. Gdy n*p < ni2 – wyciąganie
(ekstrakcja) nośników.
2
Szybkość generacji i rekombinacji jest proporcjonalna do koncentracji elektronów i
dziur. W obecności centrów generacyjno-rekombinacyjnych zwiększa się szybkość generacji i
rekombinacji (Au). Centra generacyjno-rekombinacyjne SRH (Shockley, Read, Hall).
Zjawiska kontaktowe w pp:
Trzy rodzaje kontaktów:
- kontakt pp-pp tego samego rodzaju – złącze p-n, p+-p, n+-n, l-h (styk omowy pp z
metalem),
- kontakt dwóch pp różnego rodzaju (Ge-Si) – heterozłącze
- kontakt metal – pp – złącze m-s
Te kontakty opisywane są przez charakterystykę napięciowo-prądową.
- kontakt metal-izolator-pp (MIS) – charakterystyka pojemnościowo-napięciowa.
1. Złącze p-n (dioda) – istota, opis jakościowy
Bryła pp. monokrystalicznego utworzona przez dwie graniczące ze sobą warstwy typu p i
typu n – podstawowa część składowa diód oraz tranzystorów bipolarnych i polowych.
3
W warstwie N istnieją dodatnie, nieruchome ładunki zjonizowanych atomów domieszki
donorowej oraz prawie o tej samej koncentracji ujemne ładunki ruchomych elektronów
(nośniki większościowe). Występuje tu niewielka liczba dziur – nośników mniejszościowych.
W warstwie P istnieją ujemne, nieruchome ładunki zjonizowanych atomów domieszki
akceptorowej oraz prawie o tej samej koncentracji dodatnie ładunki ruchomych dziur (nośniki
większościowe). Występuje też niewielka liczba elektronów – nośników mniejszościowych.
Obie warstwy przed zetknięciem wykazują obojętność elektryczną. Po ich zetknięciu
następuje proces dyfuzji elektronów z warstwy N do warstwy P oraz dziur z warstwy P do
warstwy N.
W obszarze granicznym warstwy N pozostają nieskompensowane ładunki dodatnie
nieruchomych centrów donorowych, zaś w obszarze granicznym warstwy P
nieskompensowane ładunki ujemne nieruchomych centrów akceptorowych.
W obszarze granicznym powstaje warstwa dipolowa ładunku, wytwarzając pole
elektryczne przeciwdziałające dyfuzji nośników większościowych = warstwa zaporowa
(ładunku przestrzennego). Napięcie wytworzone w obszarze złącza = bariera potencjału
(napięcie dyfuzyjne).
Napięcie to unosi elektrony i dziury w kierunkach przeciwnych do ich dyfuzji (te
dziury w warstwie N oraz te elektrony w warstwie P, które wskutek chaotycznego ruchu
cieplnego znajdą się przypadkowo na granicy warstwy zaporowej zostaną przechwycone
przez pole elektryczne i uniesione do obszaru przeciwnego typu zgodnie z kierunkiem pola).
Powstają dwa strumienie prądu unoszenia nośników mniejszościowych skierowane
przeciwnie do dwu strumieni prądu dyfuzji nośników większościowych.
Dla złącza nie spolaryzowanego napięciem zewnętrznym sumaryczny prąd płynący przez
złącze musi mieć wartość równą zeru, a ładunek przestrzenny wartość ustaloną.
Jdp-Jup=0; Jdn-Jun=0
W celu analizy złącza w stanie nierównowagi (polaryzacja napięciem zewnętrznym)
strukturę złącza dzielimy na trzy obszary: dwa obszary (p, n) obojętne elektrycznie oraz
obszar ładunku przestrzennego = warstwa zaporowa = warstwa zubożona (brak ruchomych
4
nośników ładunku). Z uwagi na małą koncentrację ruchomych nośników ładunku rezystancja
warstwy zubożonej >> od rezystancji obszarów obojętnych.
Prosty model złącza p-n można przedstawić w postaci trzech rezystorów połączonych
szeregowo, przy czym dominujący wpływ na kształt charakterystyki prądowo-napięciowej
złącza ma nieliniowa rezystancja warstwy zaporowej.
Możliwe są dwa rodzaje polaryzacji warstwy zaporowej.
a). Polaryzacja w kierunku zaporowym – źródło zewnętrzne ma biegunowość zgodna z
biegunowością napięcia dyfuzyjnego. Bariera potencjału zwiększa się o wartość napięcia
zewnętrznego – rośnie szerokość warstwy zaporowej (większa wartość ładunku
przestrzennego). Maleją składowe dyfuzyjne prądów elektronowego i dziurowego (nie
zmieniają się składowe unoszenia nośników mniejszościowych).
Przy polaryzacji w kierunku zaporowym składowe prądu dyfuzji nośników
większościowych maleją do zera, niezależnymi od napięcia pozostają składowe prądu
unoszenia nośników mniejszościowych.
W kierunku zaporowym płynie niewielki prąd nasycenia.
b). Polaryzacja w kierunku przewodzenia – biegun dodatni źródła połączony z warstwą P, a
ujemny z N (przeciwna biegunowość do napięcia dyfuzyjnego). Bariera potencjału maleje o
wartość napięcia zewnętrznego. Maleje szerokość warstwy zaporowej, rosną składowe prądu
dyfuzji elektronów i dziur. Składowe prądu unoszenia nośników mniejszościowych pozostają
5
na niezmienionym poziomie. Dla odpowiednio dużych wartości napięcia polaryzacji prąd
dyfuzji nośników większościowych przeważa nad prądem unoszenia nośników
mniejszościowych.
Przy polaryzacji w kierunku przewodzenia przez złącze płynie prąd dyfuzji nośników
większościowych znacznie większy niż prąd unoszenia nośników mniejszościowych.
Gęstość prądu dyfuzji proporcjonalnej do liczby nośników o energii większej od W=q(B-U):
I d  a exp[ q( B  U ) / kT ]
W stanie równowagi:
Id=Iu=aexp[-qB/kT]; Id=Iuexp(qU/kT)
Całkowity prąd:
I=Id-Iu=Iu(ex(qU/kT)-1)
lub:
I=Iu(expU/T-1) równanie Shockleya
T=kT/q potencjał elektrokinetyczny
2. Obszar ładunku przestrzennego.
W rzeczywistych złączach p-n przejście obszaru P w obszar N może być mniej lub
bardziej raptowne (zależnie od technologii). Do analizy teoretycznej przyjmuje się dwa
wyidealizowane modele rozkładu koncentracji domieszek: złącze skokowe (przejście z P do N
raptowne – metoda stopowa, epitaksja, płytkie złącze dyfuzyjne). Złącze liniowe (przejście z
P do N łagodne – głębokie złącza dyfuzyjne).
a) złącza skokowe:
- NA=ND – złącze symetryczne,
- NA>ND lub ND>NA – złącze niesymetryczne
- NA>>ND lub ND>>NA – złącze silnie niesymetryczne
Określmy rozkłady n(x), p(x) dla złącza symetrycznego NA=ND=1022 m-3. Ponieważ w
temperaturze pokojowej wszystkie atomy domieszek są zjonizowane, więc koncentracje
nośników większościowych w obszarach obojętnych elektrycznie są równe koncentracjom
domieszek: nn=ND, pp=NA. Ponieważ:
pp*np=ni2, nn*pn=ni2, ni=1016 m-3 (Si)
pn=ni2/nn=1010 m-3, np=ni2/pp=1010 m-3 - koncentracje nośników mniejszościowych; w
obszarze granicznym nie może być skokowej zmiany koncentracji nośników (1022-1010 m-3).
Wskutek dyfuzji ustalają się więc rozkłady n(x) i p(x) z łagodnym przejściem od
dużych do małych wartości (oba wykresy przetną się dla x=0 przy wartości n = p = n i).
Rozkłady te są symetryczne względem poziomu ni.
6
W obszarze ograniczonym współrzędnymi –lp oraz ln zakłócona jest obojętność
elektryczna. Po stronie warstwy P ładunek zjonizowanych domieszek akceptorowych –qNA>>
od ładunku większościowych nośników (dziur), a ładunek nośników mniejszościowych
(elektronów) ≈ 0. Po stronie warstwy N ładunek zjonizowanych domieszek donorowych
qNd>> od ładunku nośników większościowych (elektronów), a ładunek nośników
mniejszościowych (dziur) ≈ 0.
W pierwszym przybliżeniu można przyjąć, że w warstwie zaporowej istnieją
wyłącznie ładunki zjonizowanych domieszek = przybliżenie warstwy zubożonej =
przybliżenie deplecyjne. Jest ono słuszne dla złącza symetrycznego, mniej dla
niesymetrycznego, a najmniej dla silnie niesymetrycznego.
7
Jaki jest rozkład gęstości ładunku przestrzennego, jaki jest rozkład natężenia pola i
potencjału, jaka jest szerokość warstwy zaporowej…analitycznie?
Zależność pomiędzy polem i rozkładem gęstości ładunku określa prawo Gaussa:
E 
 2


lub

2
x  s

x
s
, r-nie Poissona,  – potencjał, natężenie pola E  

x
EMax=-qNAlp/s=-qNDln/s – poprzez scałkowanie ładunku
Napięcie dyfuzyjne (całkowanie natężenia pola):
B=1/2Emax*ld
Szerokość warstwy zaporowej ld=lp+ln:
l d  2 s ( N D  N A ) B / qN D N A
dla zlacza niesymetry cznego :
l d  2 s B / qN D N A  N D
l d  2 s B / qN A N D  N A
W złączu niesymetrycznym o szerokości warstwy zaporowej decyduje koncentracja
domieszek w obszarze słabiej domieszkowanym.
Napięcie dyfuzyjne można wyznaczyć z warunku równowagi prądu dyfuzji i prądu unoszenia
dla dziur lub elektronów:
8
 B  T ln( p p / pn );  B  T ln(nn / n p );  B  T ln( N A N D / ni2 )
Np. w temperaturze pokojowej NA=ND=1022 m-3,
Dla złącza krzemowego B=670 mV, dla złącza germanowego 300 mV.
W przypadku stanu nierównowagi termodynamicznej:
l d  2 s ( N D  N A )( B  U ) / qN D N A
Rys. 3.12. Wykresy rozkładu gęstości ładunku elektrycznego (a), natężenia pola (b) i
potencjału (c) dla złącza niesymetrycznego
9
b) złącze liniowe
- stan równowagi termodynamicznej (U=0)
l d  3 12 s B / qa ; Emax  1.5 B / l d ;  B  2T ln(al d / 2ni ) ; a=dNAD/dx; =qax
- stan nierównowagi termodynamicznej (U≠0)
l d  3 12 s ( B  U ) / qa
Złącze rzeczywiste:
10
3. Energetyczny model pasmowy złącza p-n
- poziom Fermiego ma jedną stałą wartość w całym obszarze złącza (warunek równowagi
termodynamicznej)
- w obszarach obojętnych elektrycznie (poza warstwą zaporową) nie zmieniają się
koncentracje elektronów i dziur, tzn. położenie poziomu Fermiego w paśmie zabronionym
pozostaje takie, jakie było w oddzielnych warstwach P, N.
Skok poziomu energetycznego dna pasma przewodnictwa oraz wierzchołka pasma
walencyjnego reprezentuje barierę potencjału w złączu, a płynna zmiana energii potencjalnej
elektronów i dziur zachodzi w obszarze warstwy zaporowej.
Energia elektronów rośnie w kierunku „do góry” rysunku, dziur – „do dołu” rysunku.
W stanie równowagi składowe prądu dyfuzji i unoszenia kompensują się oddzielnie
dla elektronów i dziur = liczba elektronów w warstwie N dysponujących energią większą niż
energia bariery jest równa liczbie elektronów w warstwie P. Podobnie z dziurami.
W stanie nierównowagi składowe prądu dyfuzji nośników większościowych i
unoszenia nośników mniejszościowych nie kompensują się. Nie występuje poziom Fermiego
w warstwie zaporowej – obszar o zakłóconej równowadze termodynamicznej – quasi poziom
Fermiego, oddzielny dla elektronów i dla dziur (rys. 3.19 b, c).
11
4. Charakterystyka prądowo-napięciowa
a) Przybliżenie pierwszego stopnia
- pole elektryczne istnieje tylko w warstwie zaporowej; rezystancje obszarów obojętnych
elektrycznie są równe zero, a nośniki wstrzykiwane do tych obszarów są przenoszone tylko na
skutek dyfuzji,
12
- pomija się zjawiska generacji-rekombinacji w warstwie zaporowej,
- poziom wstrzykiwania nośników jest mały (koncentracja nośników nadmiarowych
mniejsza od koncentracji domieszek),
- pomija się zjawiska przebicia.
Do obszarów N, P są wstrzykiwane nośniki mniejszościowe nadmiarowe (dziury do
warstwy N oraz elektrony do warstwy P), dyfundujące w głąb tych warstw i rekombinujące z
nośnikami przeciwnego typu (koncentracja nośników nadmiarowych maleje przy oddalaniu
się od krawędzi warstwy zaporowej).
W stanie ustalonym rozkłady ładunków nadmiarowych nie zmieniają się; każdemu aktowi
rekombinacji musi towarzyszyć proces uzupełniania ładunku. Po rekombinacji nadmiarowej
dziury z elektronem w warstwie N następuje wstrzyknięcie brakującej dziury z warstwy P
oraz dopływ elektronu z głębi warstwy N = dopływ elektronu z obwodu zewnętrznego (tak
zachowana jest stałość sumarycznego prądu dziur i elektronów w dowolnym przekroju złącza
p-n (rys. 3.20c).
Przy małym poziomie wstrzykiwania nośników poza warstwą zaporową obszary P, N
są elektrycznie obojętne = prądy nośników wstrzykiwanych mają charakter dyfuzyjny.
Całkowity prąd płynący przez złącze p-n można wyznaczyć przez dodanie prądów
elektronów i dziur na granicy warstwy zaporowej.
dn p
dp
Całkowity prąd: J  J dn | x' 0  J dp | x' 0  qDn
|
qD p n' | x' 0
' x ' 0
dx
dx
Koncentracje nośników nadmiarowych wstrzykiwanych na jednej ze ścian bryły
półprzewodnika:
n p  n po  n 'p (0) exp(  x / Ln ); pn  pno  pn' (0) exp(  x / L p )
npo, pno – koncentracje nośników mniejszościowych w stanie równowagi, n’p(0), p’n(0) –
koncentracje nośników mniejszościowych nadmiarowych dla x=0, Ln, Lp – długość dyfuzyjna
elektronów, dziur.
Stąd: J  qDn n 'p (0) / Ln  qD p pn' (0) / L p
Aby wyznaczyć koncentracje nośników nadmiarowych trzeba posłużyć się statystyką
Boltzmanna:
n 'p (0)  n po [exp( U / T )  1]; p n' (0)  p no [exp( U / T )  1]
skąd całkowity prąd:
Dn n po D p p no
J  q[

][exp(U / T )  1]  J s [exp(U / T )  1] lub L  D , n po  ni2 / p p
Ln
Lp
p n 0  ni2 / nn , p p  N A ; nn  N D
J  qni2 (
Dn 1

n NA
Dp 1
)[exp(U / T )  1]  J s [exp(U / T )  1]
 p ND
U ze znakiem „+” – kierunek przewodzenia, U ze znakiem „-„ dla kierunku zaporowego
Przy polaryzacji w kierunku zaporowym: J = -Js, a dla złącza niesymetrycznego (NA>>ND):
Dp 1
J s  qni2
 p ND
Charakterystyka napięciowo-prądowa złącza niesymetrycznego określona jest przez
właściwości nośników mniejszościowych (Dp, p) w warstwie słabiej domieszkowanej i
koncentracje domieszek w tej warstwie.
Warstwa słabiej domieszkowana – baza, silniej domieszkowana – emiter złącza p-n.
13
b). Przybliżenie drugiego stopnia
- w obszarze warstwy zaporowej mają miejsce zjawiska generacji-rekombinacji i część
nośników większościowych dyfundujących przez warstwę zaporową ulega rekombinacji,
- wzrasta liczba nośników mniejszościowych, unoszonych w polu elektrycznym warstwy
zaporowej wskutek generacji par elektron-dziura w obszarze tej warstwy.
Przy pracy złącza w kierunku zaporowym generacja przeważa nad rekombinacją. Gęstość
prądu generacji:
1 n 2 s N A  N D
J g  qGld ; G  ni / 2  np / 2 ; J g  q i
( B  U ) ; zas
2 
q NAND
Jg
Js

1
2 ni
2 s N D
( B  U )  N D l d / 2ni L p
q D p p
Jg/Js zależy od koncentracji nośników samoistnych (szerokości pasma zabronionego), od
koncentracji domieszek w bazie złącza oraz od ilorazu szerokości warstwy zaporowej i drogi
dyfuzji.
14
Pominięcie prądu Jg (przybliżenie pierwszego stopnia) jest słuszne dla złączy Ge, a zupełnie
niesłuszne dla złączy Si i GaAs.
Przy pracy złącza w kierunku przewodzenia do warstwy zaporowej są wstrzykiwane
nośniki i proces rekombinacji przeważa nad procesem generacji. W stanie nierównowagi:
n
np  ni2 exp(U / T ) i R  i exp(U / 2T )
2
Gęstość prądu rekombinacji:
1 n
J r  qRl d  q i l d exp(U / 2T ) oraz
2 
J r 1 N D ld

exp( U / 2T )
J d 2 ni L P
dla U  0 J r / J d  J g / J s
Prąd rekombinacji jest mniejszy niż prąd dyfuzji w złączu Ge, ale >> w złączu Si i GaAs.
15