Wykład 2

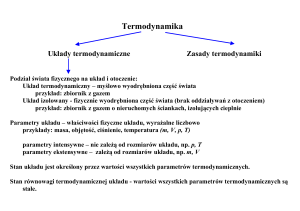
Wykład 2
Przemiany termodynamiczne
Przemiany odwracalne:
1. izobaryczna p = const
2. izotermiczna T = const
3. izochoryczna V = const
4. adiabatyczna  = const
5. izentropowa S = const
6. politropowa m = const
Przemiany nieodwracalne:
7. dławienie
8. mieszanie
9. tarcie
10. wymiana ciepła
Badając stan równowagi czynnika podlegającego przemianom zakłada się,
że w całej jego masie jest jednakowa temperatura, ciśnienie i gęstość,
a inne parametry takie jak U – energia wewnętrzna, I – entalpia oraz
S – entropia są stabilne. Odwracalność przemian polega na możliwości
powrotu do początkowych parametrów stanu gazu ze zwróceniem lub
pobraniem energii cieplnej.
Przemiana izobaryczna (p = const)
V1
T1
a) równanie przemiany: V  T
2
2
b) praca zewnętrzna: dL=p dV
L = p (V2 – V1) = MR (T2 – T1)
c) praca techniczna: dLt=-Vdp
Lt = V (p1 – p2) = 0
d) ciepło doprowadzone w czasie przemiany: dQ=dI=McpdT Q=Mcp(T2-T1)
e) sprawność termiczna:

MR(T2 - T1 ) c p - c v  - 1
praca



ilość doprowadzo nego ciepla Mc p (T2 - T1 )
cp

Dla gazu jednoatomowego =1,67, czyli =0,41, dla dwuatomowego
=1,4, czyli =0,286
T2
f) przyrost entropii podczas przemiany: S2-S1 = M c p ln T
1
Przemiana izochoryczna (V = const)
p1
T1
a) równanie przemiany: p  T
2
2
b) praca zewnętrzna: L=0, bo dV=0
c) praca techniczna: Lt = V(p1-p2)
d) ciepło doprowadzone w czasie przemiany: dQ=dU=McvdT
e) przyrost entropii: S2-S1=Mcvln
Q=Mcv(T2-T1)
T2
T1
10
Przemiana izotermiczna (T = const)
a) równanie przemiany: p1V1 = p2V2
V2
p
=p1V1ln 1
V1
p2
p1
c) praca techniczna: Lt=MRT1ln p = L
2
b) praca zewnętrzna: L=p1V1ln
V2
p
p
= -p1V1 ln 2 = p1V1 ln 1 = L
V1
p1
p2
V
p
e) przyrost entropii: S2-S1=MR ln 2 = MR ln 1
V1
p2
d) ciepło doprowadzane: Q=p1V1 ln
Przemiana adiabatyczna (dQ = 0)
charakteryzuje się brakiem wymiany ciepła pomiędzy czynnikiem a źródłami
zewnętrznymi, przy czym zarówno dQ=0 i Q=0. Ponieważ dQ=0 przy T>0,
czyli dS=0, a więc S=const. Przemiana adiabatyczna odwracalna jest przemianą,
podczas której entropia jest stała, czyli jest to przemiana izentropowa
(S = const).
W odróżnieniu od niej stosujemy określenie przemiana adiabatyczna dla
takiej, przy której wykładnik izentropy  
cp
cv
=const. Podczas takiej przemiany
brak jest wymiany ciepła z otoczeniem, a wytworzone ciepło tarcia powoduje
podwyższenie energii wewnętrznej czynnika.
1-
a) równania przemiany: pV=const, TV-1=const, T p  = const,
b) praca zewnętrzna podczas przemiany adiabatycznej

MRT1   p 2
L  U 1 - U 2  Mc v (T1 - T2 ) 
1-
  1   p 1




 -1


  MRT1

 1

 V
1 -  1
  V2
 -1



 MRT  T 
1

1- 2 

  1  T1 

c) praca techniczna podczas przemiany adiabatycznej
Lt = I1-I2 = Mcp(T1-T2) =Mcv(T1-T2) =L
7. Przemiana politropowa
W tej przemianie istnieje wymiana ciepła dQ=McdT, przy czym średnie ciepło
właściwe „c” dla danej politropy jest stałe i równe: c = cv + p
dV
m-
 cv
dt
m -1
Wykładnik politropy m, stały dla danej rodziny przemian, może być dowolną
liczbą rzeczywistą wiekszą lub mniejszą od . Podczas przemiany politropowej
wykładnik m jest stały.
11
a) równania przemiany: pVm=const, TVm-1=const, T p
b) praca zewnętrzna podczas przemiany politropowej

MRT1   p 2
L
1- 
m  1   p1




m -1
m


  MRT1 1 -  V1
 m  1   V2





m -1
 MRT
1

 m  1
1-m
m
= const,
 T2 
1 - T 

1
c) praca techniczna podczas przemiany adiabatycznej
Lt = I1-I2 =mL
d) ciepło doprowadzone: Q = Mc(T2-T1)
e) przyrost entropii: S2-S1=Mc ln
T2
T1
Zależność pomiędzy parametrami stanów 1 i 2 przemiany politropowej
p 2  V1

p1  V2
m
m

 T  m -1
   2 

 T1 
Jeżeli 1<m< to c<0, co jest równoznaczne z tym, że energia wewnętrzna
układu maleje przy wykonywaniu pracy większej od ilości ciepła
doprowadzanego. Wykładnik politropy można wyznaczyć analitycznie
przy pomocy wzoru:
p2
p1
m
V
lg 1
V2
lg
Typowe przemiany politropowe:
Wykładnik Ciepło
politropy właściwe
0
cp
1


0
cv

Równanie
przemiany
p = const
pV=RT=const
pV = const
V = const
Przemiany
izobaryczne substancji dowolnych
izotermiczne gazów doskonałych
izentropowe gazów doskonałych
izochoryczne substancji dowolnych
Dławienie:
adiabatyczne rozprężanie płynu w układzie przepływowym bez odprowadzania
na zewnątrz układu pracy technicznej. Może być spowodowane gwałtownym
przewężeniem kanału, jak np. zawór, zwężka pomiarowa (niequasistatyczna)
lub porowatą przegrodą (może być quasistatyczna). Szczegóły związane z tym
procesem zostaną przedstawione podczas omawiania działu Przepływy ściśliwe.
12
Mieszanie:
chodzi tu głównie o mieszanie dwóch strumieni gazów wilgotnych w
szczególności powietrza (mieszanie izobaryczno-adiabatyczne), które zostanie
omówione w dziale Gazy wilgotne.
Tarcie:
ze zjawiskiem tarcia mamy najczęściej do czynienia przy przepływie
rzeczywistego płynu z dużymi prędkościami. Bliżej zostanie ono wyjaśnione
przy omawianiu zagadnień związanych z przepływami przez dysze.
Wymiana ciepła:
Wszystkie aspekty związane z tym tematem zostaną omówione w odrębnym
dziale związanym z wymianą ciepła (przewodzenie, przenikanie, przejmowanie,
promieniowanie)
Obiegi termodynamiczne
Obiegiem (lub cyklem) termodynamicznym nazywamy zespół
kolejnych przemian, po wykonaniu których stan rozpatrywanego
układu powraca do stanu początkowego. Geometrycznie obieg jest
przedstawiony w postaci linii zamkniętej.
Obieg jest odwracalny, jeżeli składa się składa wyłącznie z przemian
odwracalnych. Nieodwracalność chociaż jednej przemiany czyni
obieg nieodwracalnym.
Praca obiegu jest równa ciepłu obiegu: Lob=Qob
Praca i ciepło obiegu są przedstawiane na wykresach p-V i T-S
polem ograniczonym przemianami tworzącymi obieg. Dla obiegu
silnika zgodnego z ruchem wskazówek zegara na wykresach
o współrzędnych p-V i T-S praca obiegu jest dodatnia. Dla obiegu
urządzenia chłodniczego lub obiegu pompy ciepła, przeciwnego do
ruchu wskazówek zegara praca obiegu jest ujemna.
Parametry obiegów:
a) ciepło obiegu Qob obejmuje ciepło wynikłe z wymiany ciepła Qzob
oraz zawsze dodatnie ciepło tarcia Qwob
Qob = Qzob + Qwob
13
b) ciepło obiegu spowodowane wymianą ciepła Qzob jest równe
różnicy między ciepłem Q1 doprowadzonym do obiegu a
bezwzględną wartością ciepła Q2 odprowadzonego z obiegu
Qzob = Q1 – |Q2|
c) praca obiegu składa się z zewnętrznej pracy obiegu Lzob oraz pracy
na pokonanie oporów tarcia obiegu Lwob
Lob = Lzob + Lwob
d) praca zewnętrzna obiegu równa jest ciepłu wynikłemu z wymiany
ciepła:
Lzob = Qzob = Q1 - |Q2|
e) praca na pokonanie oporów tarcia jest równa ciepłu tarcia obiegu
Lwob = Qwob > 0
f) sprawność cieplna obiegu silnika jest to stosunek pracy zewnętrznej
obiegu do ciepła doprowadzonego do obiegu
t 
Q
q
L zob
1- 2 1- 2
Q1
Q1
q1
(14)
gdzie: q2 , q1 – gęstości strumienia cieplnego
g) wydajność obiegu chłodniczego jest to stosunek ciepła
odprowadzanego od źródła ciepła o niższej temperaturze do
bezwzględnej wartości pracy zewnętrznej obiegu
p 
Q1
Q1
q1


L zob
Q 2 - Q1 q 2 - q 1
(15)
14
h) wydajność obiegu pompy jest to stosunek ciepła doprowadzanego
do źródła ciepła o wyższej temperaturze do bezwzględnej wartości
pracy zewnętrznej obiegu
p 
Q2
L zob

Q2
Q 2 - Q1

q2
q2 - q1
(16)
Podstawowe obiegi termodynamiczne:
1. Obieg Carnota
Obieg Carnota składa się z dwóch izoterm i dwóch adiabat.
Rys. 4. Obieg Carnota przedstawiony na wykresach p-V i T-S
Praca obiegu: Lob = Q1 – |Q2|
Sprawność obiegu:
η
Q1 - Q2
Q1
 1-
Q2
Q1
Ponieważ dla adiabaty dQ = T dS, to Q1 = T2(S3-S2) oraz
|Q2| = T1(S4 – S1). Ponieważ S3 = S4 i S1 = S2, to
T
ostatecznie: η  1 - T12 . W obiegu Carnota o sprawności decydują
temperatury źródeł ciepła. Sprawnośc silnika Carnota jest tym wyższa
im przy wyższej temperaturze ciepło jest doprowadzane, a przy
niższej odprowadzane. Sprawność cieplna nieodwracalnego obiegu
silnika jest mniejsza od sprawności obiegu silnika Carnota między
źródłami ciepła o tych samych temperaturach. Przykładowo, gdy
temperatury źródeł wynoszą: górnego T1=60oC a dolnego T2=-60oC,
to = 1- 213/333 = 0,36
15
2. Obieg Joule’a
Obieg silnika powietrznego, turbiny gazowej, silnika
odrzutowego. Składa się z dwóch adiabat i dwóch izobar.
Rys. 5. Obieg Joule’a przedstawiony na wykresach p-V i T-S
ciepło dostarczone do obiegu: Q1 = Mcp(T3 – T2),
ciepło odprowadzone: |Q2| = Mcp(T4 – T1),
praca wykonana przez obieg:
L =Q1 - |Q2|=Mcp(T3 – T2) - Mcp(T4 – T1),
sprawność obiegu:  
L zob
Q1
1-
Q2
Q1
1-
Wprowadzając pojecie sprężu  =
oraz stopnia sprężania  =
V1
V2
T4 - T1
T3 - T2
V

  1
p1 p4  V2
p2
p3





V
  4
 V3





, przy czym  = 
po prostych przekształceniach można otrzymać wzór na sprawność
termiczną obiegu Joule’a w postaci: t =
1-
T4
T3
1
1
 -1


 1-
1
  -1
Odwrotnością obiegu Joule’a jest obieg sprężarki tłokowej,
który będzie omówiony w późniejszym terminie.
16
3. Obieg Otto
Stosowany jest przy porównywaniu silników tłokowych
spalinowych wolnobieżnych gaźnikowych z zapłonem iskrowym.
Składa się z dwóch izochor i dwóch adiabat.
Rys. 6. Obieg Otto przedstawiony na wykresach p-V i T-S
ciepło doprowadzone do obiegu: Q1 = Mcv(T3-T2),
ciepło odprowadzone: |Q2| = Mcv(T4-T1),
praca obiegu: L = Q1 – |Q2|,
sprawność obiegu: =
1-
Q2
Q1
1-
1
 -1
1
1-
 1


bo
T2  V1 
 
T1  V2 
 -1
p
  2
 p1



 -1

17
4. Obieg Diesel’a
Służy do porównywania wolnobieżnych silników
wysokoprężnych z zapłonem samoczynnym. Składa się z dwóch
adiabat, izobary i izochory
Rys. 7. Obieg Diesel’a przedstawiony na wykresach p-V i T-S
Ciepło doprowadzone w obiegu: Q1 = Mcp(T3 – T2),
ciepło odprowadzone z obiegu: |Q2| = Mcv(T4 – T1),
praca obiegu: L = Q1 – |Q2| = Mcp(T3 – T2) – Mcv(T4 – T1),
sprawność obiegu:
 1-
gdzie:
Mc v (T4 - T1 )
1  -1 1
 1  - 1  -1
Mc p T3 - T2



V1
V2
- stopień sprężania

V3
V2
- stopień obciążenia

p2
p1
- spręż przy czym  = 
oraz  =
cp
cv
- wykładnik adiabaty
18
5. Obieg mieszany Sabathe
Stosowany do analizy pracy szybkobieżnych silników z
zapłonem samoczynnym. Składa się z dwóch adiabat sprężania i
rozprężania, izobary i izochory, przy których dostarczane jest ciepło
oraz izochory z odprowadzeniem ciepła.
Rys. 8. Obieg Sabathe’a przedstawiony na wykresach p-V i T-S
Ciepło doprowadzone podczas obiegu:
Q1 = Q23 + Q34 = Mcv(T3-T2)+Mcp(T4-T3),
ciepło odprowadzone: |Q2| = Q51 = Mcv(T5-T1)
praca obiegu: L = Q1–|Q2| = Mcv(T3 – T2)+Mcp(T4-T3) – Mcv(T5 – T1),
sprawność :

c v T3  T2   c p T4  T3  - c v T5  T1 
c v T3  T2   c p T4  T3 
 1-
1
 k -1
 -1  - 1    - 1
p
gdzie:   p 3 - stopień izochorycznego wzrostu ciśnienia
2
V
 4
V3
- stopień obciążenia
Jeżeli =1, to obieg Diesel’a (p3 = p2).
Jeżeli =1, to obieg Otto (V4 = V3)
19
6. Obieg Humphreya
Stosowany w turbinach gazowych i silnikach odrzutowych
pulsacyjnych. Składa się z dwóch adiabat (sprężania i rozprężania),
izochory podczas której dostarczane jest ciepło i izobary, przy której
odprowadzane jest ciepło.
Rys. 9. Obieg Humphreya przedstawiony na wykresach p-V i T-S
Ciepło doprowadzone: Q1 = Mcv(T3 - T2),
ciepło odprowadzone: |Q2| = Mcp(T4 – T1),
praca obiegu: L = Q1 – |Q2|= Mcv(T3 – T2) – Mcp(T4 – T1),
sprawność obiegu:
 1- 
T4 - T1
T3 - T2
lub
1
 1- 
 1


20