File

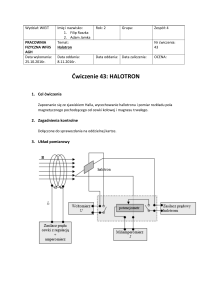
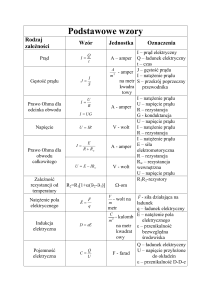
Elektrotechnika i elektronika
Zaliczenie: 1 kolokwium na 10 wykładzie na drugiej godzinie, poprawa na 15 wykładzie
Skliński – 10 wykładów z elektrotechniki
Łukjaniuk – 5 wykładów z elektroniki
Literatura
…………………….
1. Elektrotechnika – dział nauki zajmujący się podstawami teoretycznymi i zastosowaniem zjawisk
fizycznych z dziedziny elektryczności i magnetyzmu.
2. Zagadnienia wchodzące w zakres elektrotechniki:

wytwarzanie energii elektrycznej

przesyłanie energii elektrycznej,

rozdzielanie energii elektrycznej,

przetwarzanie energii elektrycznej w inne rodzaje energii,

przenoszenie za pośrednictwem fal elektromagnetycznych sygnałów elektrycznych.
3. Wielkość fizyczna – cecha zjawiska fizycznego lub własność ciała, którą można zmierzyć np.
napięcie elektryczne, temperatura, prędkość ciała itp.
Układ wielkości – zbiór wielkości fizycznych obejmujący wszystkie lub niektóre dziedziny fizyki
Wielkość pochodna – wielkość określona w zależności od wielkości pochodnych.
4. Tabela z jednostkami podstawowymi i uzupełniającymi (kąt płaski i bryłowy).
5. Tabela „dziesiętne wielokrotności miar”.
6. Rezystor idealny
Rezystor – opornik, jest dwójnikiem pasywnym (biernym), w którym zachodzi przemiana energii
elektrycznej na cieplną. Nazwa pochodzi od tego, że stawia on prądowi elektrycznemu pewien
opór, ograniczający jego natężenie. Rezystory wykonuje się z materiałów niezbyt dobrze
przewodzących.
Na schematach elektrycznych rezystor symbolizuje się białym prostokątem z dwoma
końcówkami (zaciskami).
prąd stały
prąd zmienny
7. Prawo Ohma
Napięcie na zaciskach rezystora związane jest z przepływającym przez niego prądem – prawem
Ohma:
U=Ri, i = u/R
Gdzie R jest tzw. rezystancją (o niej dalej).
i
R
u
I
I=U/R
U
Dotyczy to dowolnych przebiegów prądu i napięcia, nie tylko prądu stałego. W szczególności dla
prądu stałego
U=RI, I=U/R
R = ohmy, i = Ampery, u = volty
8. Rezystancja
Iloraz napięcia U na zaciskach rezystora i prądu I płynącego przez niego nazywa się rezystancją
(oporem) i oznacza R:
R def=U/I
Jednostką rezystancji jest 1 Ohm:
1 Ohm = V/A
Rezystory linowe mają wartość rezystancji niezależną od płynącego przez niego prądu ani od napięcia
na jego zaciskach.
9) Konduktacja
Odwrotność rezystancji R nazywamy konduktancją (pol. Przewodność)
G def = 1/R=I/U
Jednostką konduktancji jest 1 S (Simens)
1S = 1/Ohm=A/V
10) Rezystancja a wymiar ciała
Rezystancja przewodu o długości l i stałym przekroju poprzecznym o polu S wynosi
R=l/yS=pl/S
l
s
y
Gdzie:
y (gamma) - konduktywność materiału, z którego wykonany jest przewód,
p(ro)=1/y –rezystywność
Im dłuższy przewodnik, tym większa rezystancja
Im większy przekrój, tym mniejsza rezystancja
Rezystancja zależy od temperatury, gdyż zależy od niej rezystywność p
11) Przykład - rezystancja
O jakiej wartości natężenia popłynie prąd w przewodzie aluminiowym o długości l=20m i polu
przekroju poprzecznego s=1,5mm2, jeżeli pomiędzy jego końcami występuje napięcie U=0,5V?
yAl = 3,3*10^7 S/m
R=l/yAl*S = 20/3.3*10^7*1,5*10^6 =~ 0,40Ohm
I=U/R = 0,5/0,40 = 1,25A
12) Rezystor – podsumowanie
Rezystor rozprasza energię w postaci ciepła
Charakteryzuje się rezystancją R, która w przypadku rezystora liniowego nie zależy od napięcia i
prądu, ale zależy od temperatury
Prąd, napięcie i rezystancja związane są prawem Ohma.
Rezystancja R i konduktancja G=1/R cechują konkretny rezystor, podczas gdy rezystywność p i
konduktywność y=1/p cechują materiał, z którego można wykonać rezystor.
13) kondensator
Kondensator jest dwójnikiem pasywnym zachowawczym zdolnym do akumulowania energii w polu
elektrycznym
Nazwa pochodzi od tego, że „zagęszcza” (łac. Condensat) on pole elektryczne.
Na schemat elektryczny kondensator oznacza się jako dwie równoległe kreski przerywające obwód.
14) budowa i ładowanie kondensatora
Kondensator składa się z dwóch przewodzących powierzchni rozdzielonymi dielektrykiem
Przewodzące powierzchnie nazywa się okładkami lub okładzinami
Połączenie kondensatora na napięcie stałe U skutkuje jego naładowaniem, tzn. elektrony z jednej
okładki są przenoszone na drugą, wskutek czego jedna okładka zyskuje ładunek dodatni Q, a druga –
ujemny –Q ( o tej samej wartości bezwzględnej).
dielektryk
Okładki, okładziny
15) pojemność elektryczna
Pojemnością C kondensatora nazywamy iloraz ładunku Q zgromadzonego na jednej z okładzin do
napięcia U panującego między nimi
C def = Q/U
+Q
-Q
U
Jednostką pojemności jest 1 F (farad), przy czym
1F = C/V
Często używa się mF, uF i nF.
Pojemność kondensatora liniowego jest niezależna od napięcia między okładzinami.
16) pojemność a wymiary geometryczne
Pojemnośc kondensatora płaskiego wynosi
C=ErEoS/d
S-pole jednej okładki
D – odległość między okładkami
E0 (epsilon) tzw. Przenikalność elektryczna próżni (E0=~8,85*10^-12 F/m)
Er – przenikalność względna dielektryka znajdującego się między okładkami np. dla powietrza Er=~1,
dla papieru Er=~3/5
Pojemność jest tym większa, im większe pole okładek
Pojemość jest tym mniejsza, im większa odległość między okładkami.
17) Związek między prądem i napięciem
Przekształcając wzór z definicju pojemności, otrzymujemy
Q=Cu => dq/dt=C*du/dt
i
C
u
Uwzględniając, że dq/dt=i, dostajemy
I=C*du/dt
Dla napięcia stałego w czasie u=U=const, czyli
I=0
I=0
U
Wniosek: dla prądów stałych kondensator stanowi przerwą w obwodzie
18) Kondensator – podsumowanie
Nie rozprasza energii, ale magazynuje ją w polu elektrycznym
Charakteryzuje się pojemnością C, która w przypadku kondensatora liniowego nie zależy od
przyłożonego napięcia
W stanie ustalonym dla prądu stałego stanowi przerwę w obwodzie – prąd nie płynie, ale pomiędzy
jego zaciskami napięcie może być różne od zera.
19) Cewka indykcyjna
Cewka (induktor) jest dwójnikiem pasywnym zachowawczym zdolnym do gromadzenia energii w polu
magnetycznym
Nazwa pochodzi od tego, że występuje przerażenie, jako wiele nawiniętych ciasno zwojów drutu.
Druga nazwa wzięła się od tego, że indukuje się w niej napięcie zwane siłą elektromotoryczną.
Na schematach elektrycznych oznacza się ją w postaci trzech wybrzuszeń symbolizujących zwoje.
20) Pole magnetyczne
Oprócz pola elektrycznego oddrziałującego na ładunki siłą qE, istnieje pole magnetyczne oddziałujące
na ładunki siłą qv*B, gdzie v-prędkość ładunku q w polu magnetycznym B.
Intensywność pola magnetycznego określa się za pomocą wektora indukcji magnetycznej B
(jednostka 1T – tesla, przy czym 1T=Vs/m^2.
Pole magnetyczne wytwarzane jest wyłącznie przez prądy elektryczne – nie istnieją ładunki
magnetyczne.
Źródłem pola magnetycznego magnesów są prądy subatomowe.
21) Strumień magnetyczny
Strumień magnetyczny φ [fi] przenikający powierzchnię S, to iloczyn wartości wektora B i pola tej
powierzchni pomnożony przez cosinus kąta między wektorem B a wektorem prostopadłym do
rozpatrywanej powierzchni.
Φ = BS cosα
Jeżeli wektor B jest prostopadły do powierzchni S i niezmienny na tej powierzchni, to
Φ = BS
Jednostką strumienia magnetycznego jest 1 Wb (weber), przy czym
1 Wb = V*s=T*m^2
22) Indukcyjność własna
Strumień magnetyczny skojarzony Ψ z cewką równa się iloczynowi strumienia magnetycznego φ
przenikającego zwoje cewki i liczby jej zwojów z
Ψ = z*φ
Indukcyjnością własną L cewki nazywamy stosunek strumienia skojarzonego Ψ z cewką
wytworzonego przez płynący przez nią prąd I do tego prądu
L def = Ψ/ φ
Jednostką indukcyjności jest 1H (henr), przy czym
1H = Wb/Avb
23) Indukcyjność długiej cewki
Indukcyjnośc długiej cewki wynosi w przybliżeniu
L=ur*u0*z^2*S/l
Z – liczna zwojów
S – pole przekroju poprzecznego (cewki, nie drutu)
L – długośc cewki
U0 – przenikalność magnetyczna próźni (u0=4*Pi*10^-7 H/m)
Ur – przenikalność względna wnętrza cewki (rdzenia) dla powietrza ur=1, dla ferromagnetyków ur
zależy od prądu i wynosi od kilkudziesięciu do miliona
Indukcyjność jest proporcjonalna do kwadratu liczby zwojów
Cewki z rdzeniem nieferromagnetycznym są liniowe – wtedy ur=const ~=1 i ich indukcyjność nie
zależy od prądu
Cewki z rdzeniem ferromagnetycznym (np. żelaznym) są nieliniowe – ich indukcyjność zależy od
prądu, gdyż ur nie jest wielkością stałą
24) prawo faradaya
Zmienne w czasie pole magnetyczne B jest źródłem pola elektrycznego E (indukuje pole elektryczne)
To zaindukowane pole działa na ładunki z siłą qE, a więc zdolne jest wytworzyć prąd elektryczny.
Mówimy, że zmienny w czasie strumień magnetyczny indukuje siłę elektromotoryczną E (prawo
Faradaya)
ε = -d φ/dt
zwrot zaindukowanej SEM jest taki, że spowodowany przez nią przepływ prądu wytwarza strumień
przeciwdziałający zmianom strumienia pierwotnego (reguła Lorenza).
25) SEM samoindukcji
Jeżeli przez cewkę przenika strumień φ, to w każdym zwoju indukuje się SEM równa
ε1 = - d φ/dt
ponieważ zwojów jest z, to wypadkowa SEM wynosi
ε = z ε1 = -z*d φ/dt = -d(z φ)/dt = - d Ψ/dt
strumień skojarzony Ψ można wyrazić jako Li, więc dla L = const otrzymamy tz. SEM samoindukcji
cewki
ε = -L*di/dt
26) Związek między napięciem i prądem w cewce indukcyjnej
Zauważmy, że zaindukowaną SEM strzałkujemy zgodnie z prądem.
L
i
u
E
Jeżeli zastrzałkujemy napięcie przeciwnie do prądu, jak to się zwykło czynić, to wtedy u = -E, czyli
u= L*di/dt
dla prądu stałego i = I = const, więc wtedy
U=0
i
U=0
Wniosek: dla prądu stałego cewka stanowi zwarcie.
27) Cewka podsumowanie
Nie rozprasza energii, lecz magazynuje energię w polu magnetycznym
Charakteryzuje się indukcyjnością L
Cewka bez elementów ferromagnetycznych jest liniowa, a z elementami ferromagnetycznymi jest
nieliniowa,
W stanie ustalonym dla prądu stałego stanowi zwarcie – napięcie na jej zaciskach jest równe zeru, ale
może przez nią przepływać prąd.