Uploaded by
common.user1161
Równania prostych równoległych i prostopadłych - geometria analityczna
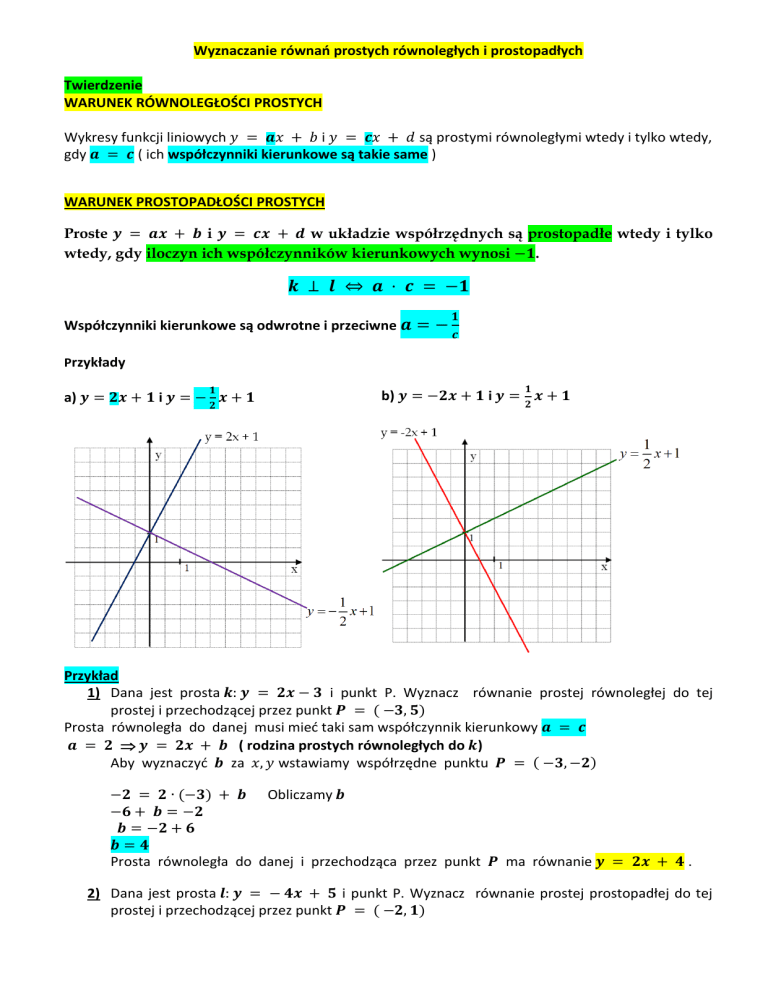
Wyznaczanie równań prostych równoległych i prostopadłych Twierdzenie WARUNEK RÓWNOLEGŁOŚCI PROSTYCH Wykresy funkcji liniowych i są prostymi równoległymi wtedy i tylko wtedy, gdy ( ich współczynniki kierunkowe są takie same ) WARUNEK PROSTOPADŁOŚCI PROSTYCH Proste i w układzie współrzędnych są prostopadłe wtedy i tylko wtedy, gdy iloczyn ich współczynników kierunkowych wynosi . Współczynniki kierunkowe są odwrotne i przeciwne Przykłady a) b) i i Przykład 1) Dana jest prosta i punkt P. Wyznacz równanie prostej równoległej do tej prostej i przechodzącej przez punkt Prosta równoległa do danej musi mieć taki sam współczynnik kierunkowy ( rodzina prostych równoległych do ) Aby wyznaczyć za wstawiamy współrzędne punktu Obliczamy Prosta równoległa do danej i przechodząca przez punkt ma równanie . 2) Dana jest prosta i punkt P. Wyznacz równanie prostej prostopadłej do tej prostej i przechodzącej przez punkt Prosta prostopadła do danej ma współczynnik kierunkowy odwrotny i przeciwny do czyli ( rodzina prostych prostopadłych do ) Aby wyznaczyć za wstawiamy współrzędne punktu Obliczamy Prosta prostopadła do danej i przechodząca przez punkt ma równanie . Równania prostych Współczynnik kierunkowy prostej przechodzącej przez punkty: i 1. Równanie kierunkowe prostej ma postać: y = ax + b gdzie a, b R 2. Postać ogólna równania prostej nazywamy równanie: Ax + By + C = 0 , gdzie A i B nie są jednocześnie równe zero. Warunek ten jest spełniony, gdy A2 + B2 > 0. 3. Równanie prostej przechodzącej przez dwa punkty A = ( x1, y1 ) i B = ( x2, y2 ), jeśli x1 x2 Przykład Oblicz współczynnik kierunkowy prostej, do której należą punkty i . ZADANIA Z ARKUSZY to współczynnik kierunkowy prostej to współczynnik kierunkowy prostej Proste są równoległe wtedy i tylko wtedy, gdy zatem musimy rozwiązać równanie: ( ich współczynniki kierunkowe są takie same ) Obliczamy deltę i pierwiastki lub stosujemy wzór skróconego mnożenia to to współczynnik kierunkowy prostej współczynnik kierunkowy prostej Proste są prostopadłe wtedy i tylko wtedy, gdy i odwrotne ) zatem musimy rozwiązać równanie: założenia: czyli ( ich współczynniki kierunkowe są przeciwne Mnożymy obustronnie przez 2m 1) Wyznaczamy współczynnik kierunkowy prostej 2) Symetralna jest prostopadła do prostej przechodzącej przez punkty kierunkowy tej prostej musi być odwrotny i przeciwny, czyli: 1) Wyznaczmy prostą przechodzącą przez punkt czyli punkt . Taka prosta ma postać: Podstawiamy za , zaś za i obliczamy . i czyli współczynnik i początek układu współrzędnych, czyli 2) Prosta prostopadła do tej prostej ma współczynnik kierunkowy odwrotny i przeciwny, czyli: to to współczynnik kierunkowy prostej współczynnik kierunkowy prostej Proste są prostopadłe wtedy i tylko wtedy, gdy i odwrotne ), zatem musimy rozwiązać równanie: Mnożymy przez ( ich współczynniki kierunkowe są przeciwne