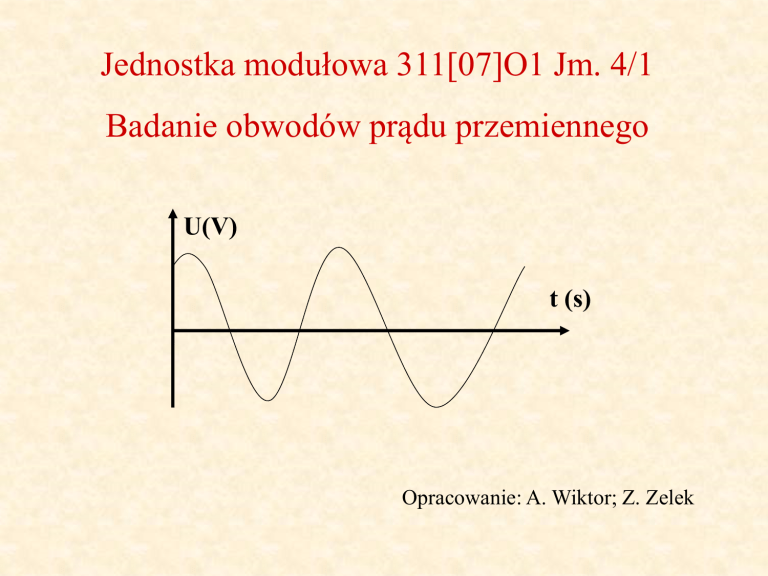
Jednostka modułowa 311[07]O1 Jm. 4/1
Badanie obwodów prądu przemiennego
U(V)
t (s)
Opracowanie: A. Wiktor; Z. Zelek
Mechanizm powstawania SEM sinusoidalnie zmiennej
E = Emax * sin
1 kratka = 1[V]
=45º E = 10*0,707 =7,07[V]
Charakterystyczne wielkości związane z prądem przemiennym
Amplituda (wartość maksymalna)
Wartość międzyszczytowa
Współczynniki obliczeniowe dla wartości:
skutecznej, średniej międzyszczytowej
najbardziej popularnych przebiegów przemiennych
Ilustracja przesunięcia fazowego pomiędzy przebiegami przemiennymi
Przebieg B opóźnia się za
przebiegiem A o kąt 45°
przebiegi są względem
siebie przesunięte w fazie.
A=+45°
Przebieg A przesunięty
względem B o 180°
Przebieg A wyprzedza
B o 90°
Przebieg B wyprzedza
A o 90°
Przebieg A w fazie z
przebiegiem B
przesunięcie 0°
Przedstawianie wielkości w obwodach prądu przemiennego
przy pomocy wektorów
Wielkości w obwodach prądu przemiennego można przedstawić za pomocą
wektorów, których długość (moduł) zależy od amplitudy, a kąty określające
zwroty wektorów uzależnione są od kątów przesunięcia pomiędzy przebiegami
czyli od faz poszczególnych przebiegów.
Przedstawienie wektorów przy pomocy liczb zespolonych (urojonych),
postać algebraiczna
Liczbą zespoloną będziemy nazywać obiekt zapisywany jako
(x+jy), gdzie j jest naszą liczbą urojoną, x i y są zwykłymi
liczbami rzeczywistymi.
j = 1 j 2 = 1
Im
(2 + j3) – postać algebraiczna
Oś urojonych
Część rzeczywista, rzut
modułu na oś rzeczywistych
Część urojona, rzut
modułu na oś urojonych.
Re
Moduł wektora (jego długość)
Oś rzeczywistych
Płaszczyzna zespolona
Liczba zespolona i odpowiadający jej wektor wodzący
mogą znajdować się w każdym miejscu płaszczyzny
zespolonej, w zależności od wartości oraz znaku części
rzeczywistej i urojonej.
Przedstawienie wektorów przy pomocy liczb zespolonych (urojonych),
postać wykładnicza
Liczbę zespoloną można przedstawić również w tzw. postaci
wykładniczej która jest równoważna postaci algebraicznej.
z = r e j
modułu wektora
Im
Liczba e – podstawa logarytmu
naturalnego e ≈ 2,71828
Argument to kąt o jaki moduł
przesunięty jest względem
dodatniej osi liczb rzeczywistych.
Re
z = 3,6 e j 57
Przykładowo dla wektora z
rysunku bo
Moduł:
Argument:
z = re2 im 2 = 22 32 = 3,6
im 3
tg =
= = 1,5; 57
re 2
Zamiana postaci algebraicznej w wykładniczą
Aby przekształcić zapis algebraiczny do równoważnego zapisu wykładniczego
należy:
1. policzyć moduł wektora,
Zapis algebraiczny liczby z
2. policzyć argument czyli kąt ,
3. zapisać liczbę w postaci wykładniczej
z = (4 j 3)
Im
Część
Częśćrzeczywista
Urojona
Część rzeczywista i urojona to przyprostokątne trójkąta
prostokątnego a moduł to przeciwprostokątna, stąd jego
długość obliczymy z twierdzenia Pitagorasa
z = re2 im 2 = 42 32 = 25 = 5
Argument to kąt o jaki moduł przesunięty jest
względem dodatniej osi liczb rzeczywistych. Obliczymy
go z wykorzystaniem funkcji tangens kąta
tg =
im 3
= = 0,75; 37
re 4
Zapis liczby z w postaci
wykładniczej
z = 5 e j 37
Zamiana postaci wykładniczej w algebraiczną
Aby przekształcić zapis wykładniczy do równoważnego zapisu algebraicznego należy
skorzystać z zapisu trygonometrycznego:
1. wstawić odpowiednio dane do postaci trygonometrycznej ,
2. policzyć i zapisać liczbę w postaci algebraicznej
Zapis wykładniczy liczby z
j 37
z = 5e
z = z ( cos j sin )
Postać trygonometryczna
Moduł wektora
Funkcja cosinus argumentu z uwzględnieniem znaku
(przebieg zmienności) dająca część rzeczywistą. Funkcja
sinus argumentu z uwzględnieniem znaku (przebieg
zmienności) dająca część urojoną zapisu algebraicznego
z = 5(cos 37 j sin 37) = 5(0,8 j 0,6) = (4 j 3)
Zapis liczby z w postaci algebraicznej
z = (4 j 3)
Działania na liczbach zespolonych (dodawanie i odejmowanie)
(możliwe jedynie w postaci algebraicznej)
Suma dwu liczb zespolonych z1=(a1+jb1) i z2=(a2+jb2) jest liczbą zespoloną
z3, której część rzeczywista jest sumą części rzeczywistych obydwu liczb a
część urojona sumą części urojonych liczb z1 i z2 .
z1 = (3 j8);
z 2 = (1 j 4)
z1 z 2 = (3 j8) (1 j 4) = (3 1) j (8 4) = (4 j 4)
Różnica dwu liczb zespolonych z1=(a1+jb1) i z2=(a2+jb2) jest liczbą
zespoloną z4, której część rzeczywista jest różnicą części rzeczywistych
obydwu liczb a część urojona różnicą części urojonych liczb z1 i z2 .
z1 = (3 j8);
z 2 = (1 j 4)
z1 z 2 = (3 j8) (1 j 4) = (3 1) j (8 4) = (2 j12)
Działania na liczbach zespolonych (mnożenie)
(możliwe w postaci algebraicznej i wykładniczej)
Mnożenie dwu liczb zespolonych z1=(a1+jb1) i z2=(a2+jb2) (postać
algebraiczna) wykonujemy jak mnożenie dwumianów w zwykłej algebrze.
z1 = (3 j8);
z 2 = (1 j 4)
z1 z 2 = (3 j8) (1 j 4) = (3 1 3 ( j 4) j8 1 j8 ( j 4)) =
(3 j12 j8 j 2 32) = ((3 32) ( j8 j12)) = (35 j 4)
Moduł iloczynu dwu liczb zespolonych z1= r1ej1° i z2= r2ej2° jest równy
iloczynowi modułów poszczególnych liczb zespolonych a argument jest
sumą argumentów poszczególnych liczb zespolonych.
z1 = 2 e
j 25
;
z1 z 2 = (2 4) e
z2 = 4 e
j ( 2550 )
j 50
= 8 e j 75
Działania na liczbach zespolonych (dzielenie)
(możliwe w postaci algebraicznej i wykładniczej)
Dzielenie dwu liczb zespolonych z1=(a1+jb1) i z2=(a2+jb2) (postać
algebraiczna), wykonujemy poprzez działanie eliminujące niewymierność w
mianowniku. W tym celu pomnożymy licznik i mianownik ilorazu obydwu
liczb przez liczbę sprzężoną do mianownika czyli liczby z2
z1 = (3 j8);
z 2 = (1 j 4);
z 2 * = (1 j 4)
Liczba sprzężona
do z2
z1 = (3 j8) = (3 j8) (1 j 4) = ((3 1) (3 j 4) ( j8 1) ( j8 j 4)) =
z 2 (1 j 4) (1 j 4) (1 j 4) ((11) (1 j 4) ( j 4 1) ( j 4 j 4))
(3 j12 j8 j 2 32) (29 j 20)
=
=
= (1,17 j1,18)
2
17
(1 j 4 j 4 j 16)
Moduł ilorazu dwu liczb zespolonych z1= r1ej1 i z2= r2ej2 jest równy
ilorazowi modułów poszczególnych liczb zespolonych a argument jest
różnicą argumentów poszczególnych liczb zespolonych.
z1 = 2 e
j 25
;
z2 = 4 e
j 50
j 25
z1 = 2 e = 2 j ( 2550) = 0,5 j 25
e
e
j 50
4
z2 4 e