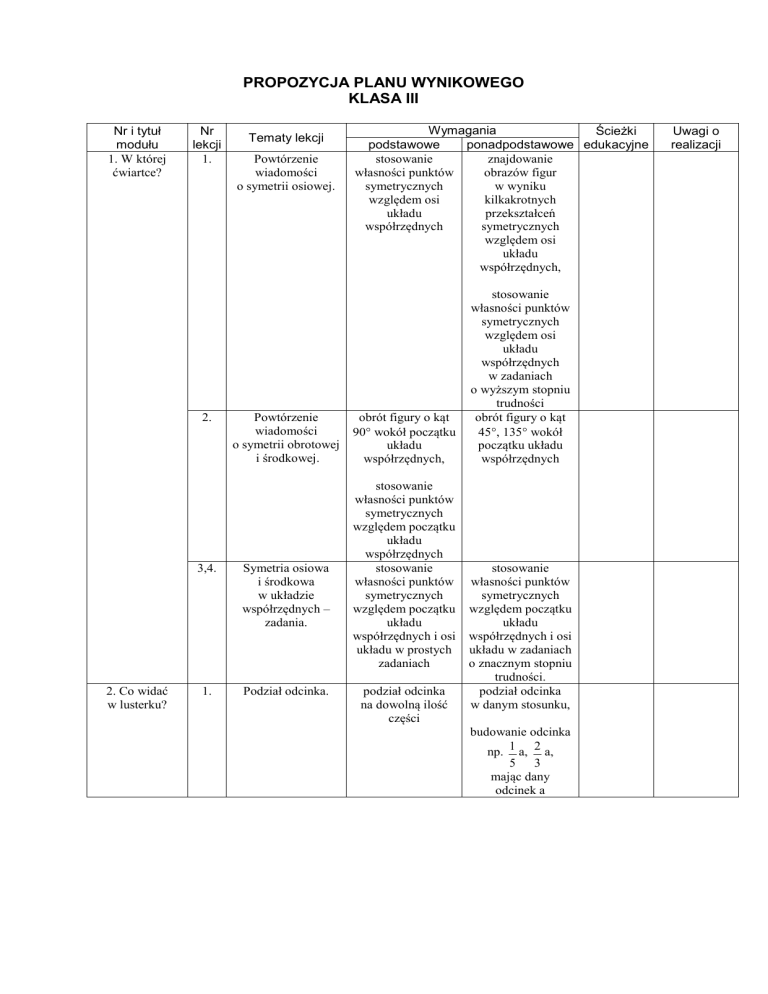
PROPOZYCJA PLANU WYNIKOWEGO
KLASA III
Nr i tytuł
modułu
1. W której
ćwiartce?
Nr
lekcji
1.
2.
2. Co widać
w lusterku?
Tematy lekcji
Powtórzenie
wiadomości
o symetrii osiowej.
Powtórzenie
wiadomości
o symetrii obrotowej
i środkowej.
3,4.
Symetria osiowa
i środkowa
w układzie
współrzędnych –
zadania.
1.
Podział odcinka.
Wymagania
Ścieżki
podstawowe
ponadpodstawowe edukacyjne
stosowanie
znajdowanie
własności punktów
obrazów figur
symetrycznych
w wyniku
względem osi
kilkakrotnych
układu
przekształceń
współrzędnych
symetrycznych
względem osi
układu
współrzędnych,
obrót figury o kąt
90 wokół początku
układu
współrzędnych,
stosowanie
własności punktów
symetrycznych
względem początku
układu
współrzędnych
stosowanie
własności punktów
symetrycznych
względem początku
układu
współrzędnych i osi
układu w prostych
zadaniach
podział odcinka
na dowolną ilość
części
stosowanie
własności punktów
symetrycznych
względem osi
układu
współrzędnych
w zadaniach
o wyższym stopniu
trudności
obrót figury o kąt
45, 135 wokół
początku układu
współrzędnych
stosowanie
własności punktów
symetrycznych
względem początku
układu
współrzędnych i osi
układu w zadaniach
o znacznym stopniu
trudności.
podział odcinka
w danym stosunku,
budowanie odcinka
np. 1 a, 2 a,
5 3
mając dany
odcinek a
Uwagi o
realizacji
2.
Jednokładność.
pojęcie punktów
i figur
jednokładnych
względem środka
jednokładności,
znajdowanie
obrazów figur
jednokładnych przy
skali 2,-3 itp.
3. Bryły z siatek.
3.
Skala
jednokładności.
4.
Jednokładność
w prostokątnym
układzie
współrzędnych.
1.
Własności
graniastosłupów
i ostrosłupów –
przypomnienie.
2.
Rysowanie
graniastosłupów
i ostrosłupów.
3.
Pole powierzchni
i objętość
graniastosłupów
i ostrosłupów.
Czytanka nr 1.
Bryły pana Platona.
Wielościany
foremne.
znajdowanie
obrazów figur
jednokładnych
względem środka
jednokładności
przy skali np.
1
3
1
, , 1
3 4
2
związek figury i jej znajdowanie środka
edukacja
jednokładnego
jednokładności na
czytelnicza
obrazu w zależności
podstawie figury
i medialna
od skali
i jej obrazu oraz
jednokładności
skali
jednokładności,
względem której
figura została
przekształcona
stosowanie
stosowanie
własności punktów
własności figur
jednokładnych
jednokładnych
względem
względem
punktu (0,0),
punktu (0,0)
w zadaniach
znajdowanie
o podwyższonym
obrazów figur
stopniu trudności
jednokładnych
względem początku
układu
współrzędnych
rozróżnianie
stosowanie
ostrosłupów
własności
i graniastosłupów,
graniastosłupów
i ostrosłupów
znajomość
w ćwiczeniach
własności
dotyczących
graniastosłupów
obliczania ilości
i ostrosłupów,
ścian, krawędzi
i wierzchołków.
pojęcie
graniastosłupów
i ostrosłupów
prawidłowych
rysowanie rzutów
zaznaczenie
graniastosłupów
przekrojów
i ostrosłupów
w graniastosłupach
i ostrosłupach
obliczanie objętości stosowanie wzorów
kultura
i pól powierzchni
na obliczanie
polska na tle
graniastosłupów
objętości i pól
tradycji
i ostrosłupów,
powierzchni
śródziemnomając dane
graniastosłupów
-morskiej
wymiary podstawy,
i ostrosłupów
wysokość bryły,
w zadaniach
wysokość ściany
o podwyższonym
bocznej
stopniu trudności
rozróżnianie brył
rysowanie siatek
edukacja
platońskich
i budowanie brył
filozoficzna
platońskich
4. Kąt w kącie.
5. Podobne
czy nie?
1.
Kąt między prostą a
płaszczyzną.
2.
Kąt miedzy dwiema
płaszczyznami.
1.
Podobieństwo brył.
zaznaczanie
i odczytywanie kąta
między prostą
a płaszczyzną
wykorzystanie
kultura
wiedzy o kącie
polska na tle
między prostą
tradycji
a płaszczyzną
śródziemnow życiu codziennym -morskiej
zaznaczanie
zaznaczanie
i odczytywanie kąta i odczytywanie kąta
między dwiema
między dwiema
płaszczyznami
płaszczyznami
w prostych
w bardziej
sytuacjach
skomplikowanych
sytuacjach
rozróżnianie brył
podobnych,
znajomość cech brył
podobnych
Skala podobieństwa.
obliczanie pól
powierzchni
i objętości brył
podobnych
na podstawie skali
podobieństwa
w prostych
sytuacjach
1.
Wartość
bezwzględna liczby.
pojęcie wartości
bezwzględnej
liczby,
2.
Rozwiązywanie
zadań dotyczących
modułu.
sporządzanie
wykresów funkcji
y = |x|
sporządzanie
wykresów różnych
funkcji
1
Przykłady funkcji
nieliniowych.
Wykres funkcji
y = a x2 + b
i jej podstawowe
własności.
pojęcie funkcji
nieliniowej,
sporządzanie
wykresów funkcji
y = a x2
sporządzanie
wykresów różnych
funkcji
nieliniowych
Graficzne
rozwiązywanie
prostych równań
nieliniowych.
rozwiązywanie
graficzne prostych
równań
nieliniowych
2.
Powtórzenie1
- praca klasowa
i jej poprawa.
6. Bez znaku.
7. Jak szybko
stygnie herbata?
obliczanie pól
powierzchni
i objętości
graniastosłupów
i ostrosłupów
podobnych
stosowanie
twierdzeń
dotyczących skali
podobieństwa
w zadaniach
o podwyższonym
stopniu trudności
kultura
polska na tle
tradycji
śródziemno-morskiej
1,2,3
2.
rozwiązywanie
prostych
nierówności
z wartością
wyznaczanie
bezwzględną
wartości
i zaznaczanie zbioru
bezwzględnej liczb,
rozwiązań
rozwiązywanie
nierówności na osi
równań typu | x | = 4
liczbowej
zapisywanie równań
na podstawie
graficznego
rozwiązania tego
równania,
rozwiązywanie
graficzne bardziej
złożonych równań
nieliniowych
edukacja
czytelnicza
i medialna
8.Poszukiwanie
trójkątów.
9.Tożsame
czy
równoważne?
10. Na kole
garncarskim.
Zastosowanie
określanie proporcji
stosowanie
edukacja
proporcji
trygonometrycznych
proporcji
filozoficzna
trygonometrycznych
kąta ostrego,
trygonometrycznych
do obliczania pól
w zadaniach
powierzchni
stosowanie
o podwyższonym
wielokątów.
proporcji
stopniu trudności
trygonometrycznych
do obliczania pól
powierzchni figur
płaskich
2.,3.
Zastosowanie
obliczanie pól
stosowanie
proporcji
powierzchni
proporcji
trygonometrycznych
i objętości
trygonometrycznych
do obliczania pól
graniastosłupów
w zadaniach
powierzchni
i ostrosłupów
o podwyższonym
i objętości
z wykorzystaniem
stopniu trudności
graniastosłupów
proporcji
i ostrosłupów.
trygonometrycznych
1.
Podstawowe
pojęcie jedynki
stosowanie
tożsamości
trygonometrycznej
podstawowych
trygonometryczne.
i innych
tożsamości
podstawowych
trygonometrycznych
tożsamości
w obliczeniach
trygonometrycznych
2.
Obliczanie wartości
przekształcanie
przekształcanie
wyrażeń z
i obliczanie
i obliczanie wartości
wartościami
wartości wyrażeń
wyrażeń
trygonometrycznymi. z zastosowaniem
o podwyższonym
tożsamości
stopniu trudności
trygonometrycznych z zastosowaniem
tożsamości
trygonometrycznych
1.
Własności walca,
rozpoznawanie brył
określanie brył
stożka i kuli.
obrotowych,
powstałych
w wyniku obrotu
wskazywanie osi
różnych figur
obrotu, wysokości
płaskich
i tworzącej walca
i stożka,
1.
wskazywanie
przekroju osiowego
2.
Siatki i przekroje
brył obrotowych.
rysowanie rzutów,
siatek i przekrojów
walca i stożka,
rysowanie rzutów,
siatek i przekrojów
brył obrotowych,
powstałych
obliczanie pola
w wyniku obrotu
powierzchni
trójkąta, prostokąta,
bocznej walca
kwadratu, dookoła
na podstawie jego
boków lub osi
przekroju osiowego,
symetrii,
obliczanie długości
obliczanie
promienia
promienia i obwodu
podstawy, mając
podstawy stożka
długości boków
przy danych
prostokąta, który
wymiarach
jest jego
powierzchni bocznej
powierzchnią
boczną
budzenie
wrażliwości
estetycznej
11. Stożek
w walcu.
1.
2.
Objętość walca
i stożka.
Pole powierzchni
walca i stożka.
rozwiązywanie
typowych zadań
na obliczanie
objętości walca
i stożka,
dostrzeganie
analogii między
graniastosłupem
i walcem,
ostrosłupem
i stożkiem
rozwiązywanie
typowych zadań
na obliczanie pola
powierzchni walca
i stożka
rozwiązywanie
nietypowych,
trudniejszych zadań
na
obliczanie objętości
walca i stożka,
sprawna zamiana
jednostek objętości
obliczanie pola
powierzchni bocznej
stożka
przy wykorzystaniu
wzorów na długość
łuku i pole wycinka,
sprawna zamiana
jednostek pola
powierzchni
3.
Czytanka nr 2.
Jak obliczyć objętość
kuli?
Objętość i pole
powierzchni walca
i stożka – zadania.
Objętość kuli
i jej pole
powierzchni.
rozwiązywanie
obliczanie objętości
zadań na obliczanie
brył wpisanych
objętości i pól
w inne bryły,
powierzchni
z wykorzystaniem sprawne korzystanie
przekrojów
z proporcji
osiowych
trygonometrycznych
i proporcji
przy obliczaniu
trygonometrycznych
potrzebnych
wielkości,
obliczanie pola
powierzchni
i objętości kuli
o danym promieniu
prace badawcze
związane z
obliczaniem
objętości i pola
powierzchni
(np. projektowanie
kartonu, do którego
zapakowane będą
puszki w kształcie
walca)
objaśnienie wzoru
na objętość kuli,
rozwiązywanie
zadań związanych
z wpisywaniem
graniastosłupów
i ostrosłupów
w kulę,
stosowanie
twierdzenia
o stosunku objętości
i pól powierzchni
figur podobnych
wykorzystanie
wiedzy
i umiejętności
w praktyce
Powtórzenie 2
- praca klasowa
i jej poprawa.
12.Algebraiczne
puzzle.
1,2,3.
1.
2.
13.Matematyczne
zaklęcia.
14. Kwadratowe
czy liniowe?
1,2.
1.
Ułamki algebraiczne.
pojęcie ułamka
sprawne stosowanie
Obliczanie wartości
algebraicznego,
wzorów skróconego
ułamków
mnożenia
algebraicznych
określanie dla jakich przy zamianie sumy
i wyznaczanie
liczb ma sens,
na iloczyn
warunku istnienia
ułamka.
skracanie
i rozszerzanie
ułamka
algebraicznego
Przekształcanie
wykonywanie
sprawne
wyrażeń
prostych działań
wykonywanie
algebraicznych.
na wyrażeniach
działań na bardziej
algebraicznych,
złożonych
wyrażeniach
obliczanie wartości
algebraicznych,
liczbowej wyrażeń
algebraicznych,
obliczanie wartości
liczbowej
zamiana sumy
w trudniejszych
algebraicznej
przykładach
na iloczyn
(złożone wyrażenia,
(wyłączanie
zmienna jest liczbą
wspólnego czynnika
niewymierną),
przed nawias,
stosowanie wzorów
zamiana sumy
skróconego
na iloczyn
mnożenia)
w trudnych
sytuacjach(metoda
grupowania)
Usuwanie
niewymierności
z mianownika.
Zapisywanie
wyrażeniami
algebraicznymi
i równaniami
sytuacji opisanych
słownie.
wykonywanie
prostych działań
na pierwiastkach,
sprawne usuwanie
niewymierności
z mianownika także
z zastosowaniem
szacowanie wartości wzoru na różnicę
liczb
kwadratów
niewymiernych,
usuwanie
niewymierności
z mianownika
w prostych
przykładach
opisywanie prostych
sytuacji
wyrażeniami
algebraicznymi
i równaniami
matematyczne
przedstawienie
złożonej sytuacji
opisanej słownie
2.
Rozwiązywanie
równań
z zastosowaniem
wzorów skróconego
mnożenia.
stosowanie wzorów
skróconego
mnożenia przy
rozwiązywaniu
równań,
rozwiązywanie
prostych zadań
tekstowych
za pomocą równań
3,4.
15. Jaka
temperatura
wystarczy ?
1,2.
Rozwiązywanie
układów równań
zawierających wzory
skróconego
mnożenia.
Rozwiązywanie
nierówności.
rozwiązywanie
układów równań,
zawierających
wzory skróconego
mnożenia trzema
metodami,
rozwiązywanie
prostych zadań
tekstowych za
pomocą układów
równań
pojęcie zbioru
rozwiązań
nierówności,
przedstawianie
zbioru rozwiązań
nierówności
na osi liczbowej,
16. Kto lepszy?
sprawne
rozwiązywanie
równań
z zastosowaniem
wzorów skróconego
mnożenia,
sprawne stosowanie
równań do
rozwiązywania
zadań tekstowych
sprawne
rozwiązywanie
układów równań
z zastosowaniem
wzorów skróconego
mnożenia,
sprawne stosowanie
układów równań
do rozwiązywania
zadań tekstowych
sprawne
rozwiązywanie
nierówności
ze wzorami
skróconego
mnożenia ,
rozwiązywanie
nierówności
z zastosowaniem
wzorów skróconego
mnożenia
graficzne
rozwiązywanie
nierówności
i układów
nierówności
w układzie
współrzędnych,
nierówność
podwójna
rozwiązywanie
złożonych zadań
za pomocą
nierówności
3.
Zastosowanie
nierówności
do rozwiązywania
zadań tekstowych.
opisywanie
nierównością
prostych zadań
tekstowych
1.
Przedstawianie
danych
statystycznych-diagramy
łodygowo-listkowe.
zbieranie,
organizowanie
danych konkretnego
rodzaju,
sporządzanie
diagramów
łodygowolistkowych,
odczytywanie
danych
z diagramów
łodygowolistkowych
właściwa analiza
danych,
określanie pozycji
interesującej nas
danej na tle całego
zestawu danych,
określanie typowych
danych
i danych
odbiegających
od normy
wykorzystanie
wiedzy
i umiejętności
w praktyce
edukacja
medialna
budzenie
wrażliwości
estetycznej
2.
Liczby
charakterystyczne
dla zestawu danych –
diagram pudełkowy.
określanie liczb
reprezentujących
zestaw danych,
wnioskowanie
na temat badanych
danych
edukacja
medialna
stawianie hipotez
i wyciąganie
wniosków
na podstawie
zebranych danych,
edukacja
medialna
(roczniki
statystyczne,
gazety),
porównywanie
wyników
z obserwacji zjawisk
tego samego typu
na podstawie
diagramów
opisywanie
doświadczeń
losowych rysunkiem
drzewka,
ścieżka
regionalna
obliczanie rozstępu,
mediany, kwartyli,
sporządzanie
i odczytywanie
diagramów
pudełkowych
3.
17. Czy warto
grać w tę grę?
1.
Prezentowanie
danych.
Rozumowanie
statystyczne.
Doświadczenie
losowe, ocena szans.
obserwowanie
możliwych
wyników serii
doświadczeń
poznanie
różnych
źródeł
informacji
o świecie
określanie
wszystkich
możliwych
wyników danego
doświadczenia
losowego,
2,3.
Powtórzenie 3
- praca klasowa
i jej poprawa.
Badanie
kilkuetapowych
doświadczeń
losowych.
porównywanie
wyników obserwacji
zjawisk tego samego
typu na podstawie
tabelek
stawianie hipotez
i ich weryfikacja
wykorzystanie
wiedzy
i umiejętności
w praktyce
1,2,3.
Lekcje
powtórzeniowe.
Ciekawe
problemy.
Opracowanie: Elżbieta Wyłuda i Alina Zabłocka w oparciu o program „Matematyka 2001”