Sposoby doprowadzania i odprowadzania energii z układu

Sposoby doprowadzania i wyprowadzania energii
W zagadnieniach technicznych - cztery sposoby przekazywania energii:
1) za pomocą prądu elektrycznego,
2) przez wykonanie pracy mechanicznej,
3) przez przepływ ciepła,
4) za pośrednictwem strumienia substancji.
Moc elektryczna Nel zmierzona watomierzem
wyraża strumień energii doprowadzonej do układu,
jeśli w układzie działa silnik lub grzejnik elektryczny,
lub wyprowadzanej z układu,
jeżeli w układzie działa generator elektryczny.
Praca mechaniczna
może być wykonana w urządzeniach technicznych za pośrednictwem:
- tłoczyska poruszającego się ruchem posuwisto-zwrotnym
w maszynach tłokowych,
- obracającego się wału w maszynach wirnikowych.
Pracę wykonaną przez układ uważa się za dodatnią.
Praca wykonana na układzie ma znak ujemny.
Maszyna pobierająca energię chemiczną, elektryczną itp.
i wykonująca w sposób ciągły dodatnią prace nazywa się silnikiem.
Maszynę napędzaną silnikiem (np. pompę, wentylator)
nazywamy maszyną roboczą.
Przepływ ciepła może wystąpić po zetknięciu układu z ciałem
mającym inną temperaturę
lub bez zetknięcia, przez promieniowanie.
Ciepło pochłonięte przez układ uważamy za dodatnie,
ciepło oddane ma znak ujemny.
Procesy w przyrodzie często przebiegają z udziałem tarcia.
Pokonanie tarcia wymaga wykonania pracy,
jednak ta praca zmienia energię układu tak,
jak przy pochłanianiu równoważnej ilości ciepła.
Tarcie zamienia więc efekty energetyczne wykonywania pracy
na efekty wywołane przez pochłanianie ciepła
Lf = Qf
gdzie:
Lf - praca przeciwko oporom tarcia,
Qf - ciepło tarcia.
Sposoby doprowadzania i wyprowadzania energii
a) za pomocą prądu elektrycznego,
b) przez wykonanie pracy mechanicznej – na sposób pracy,
c) przez przepływ ciepła – na sposób ciepła,
d) za pośrednictwem strumienia substancji.
Sposoby doprowadzania i odprowadzania energii z układu
1) na sposób ciepła
prawo Pẻcleta - dot. przenikania ciepła
.
Q
= k ∙ A ∙ Δt
gdzie
.
k A Δt Q
Δt = ( tF,1 – tF,2 )
strumień ciepła przenikającego przez przegrodę, [W]
współczynnik przenikania ciepła, [W/(m2 K)]
powierzchnia przegrody, [m2]
różnica temperatury między płynami, [K]
W fizyce budowli (wg metodologii):
strumień ciepła przenikający przez przegrodę budowlaną
.
Q tr
czyli
.
Q tr
= U ∙ Ae ∙ ( Θi - Θe )
= Htr ∙ ( Θi - Θe )
gdzie współczynnik straty mocy cieplnej przez przenikanie
Htr = U ∙ Ae
nie zależy od różnicy temperatury
2) za pośrednictwem strumienia substancji
.
strumień objętości płynu
V
[m3/s]
gęstość płynu
ρ
[kg/m3]
strumień masy płynu
.
m
=
.
V
∙ρ
[kg/s]
stan energetyczny płynu określa entalpia właściwa
i = cp ∙ t
.
strumień energii płynu
I
.
I
lub
.
I
.
=
V
=
V
.
=
[J/kg]
.
m
∙ i
∙ ρ ∙ cp ∙ t
∙ ρ ∙ cp ∙ Θ
[W]
Przykładowe bilanse energii
Równanie bilansu energetycznego
Ed = ΔEu + Ew
Ed - energia doprowadzana do układu
ΔEu - przyrost energii układu
Ew - energia wyprowadzana z układu
Przypadki :
1) stan równowagi termodynamicznej
ΔEu = U2 – U1 = 0,
czyli
Ed = Ew
2) stan nieustalony
np. energia doprowadzana zostaje
akumulowana w przegrodzie budowlanej,
bez wyprowadzania energii z układu
Ed = ΔEu , bo
Ew = 0
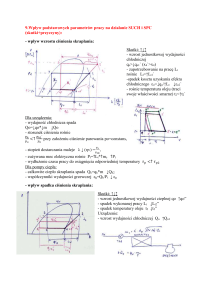
1.1. Budynek, pomieszczenie
w stanie równowagi termodynamicznej
Oznaczenia:
temperatura powietrza zewnętrznego
Θe = var
temperatura powietrza wewnętrznego
Θi = idem
.
energia str. powietrza usuwanego
I v,i
energia str. powietrza doprowadzanego
I v,e
ciepło doprowadzane grzejnikiem
.Q d
strata ciepła przez przenikanie
.
.
=
=
V
.
V
∙ ρ ∙ cp ∙ Θi
∙ ρ ∙ cp ∙ Θe
.
.
Q tr
= A ∙ U ∙ (Θi - Θe)
Z bilansu energii dla stanu równowagi wynika
Ed = Ew
czyli
.
.Q d
+
.
I v,e
=
.
.
I v,i
+
Q tr
skąd
.
.Q d
czyli
.
.Q d
=
.
I v,i
-
.
I v,e
.
+
Q tr
= ( Htr + Hve ) ∙ (Θi - Θe)
gdzie niezależne od różnicy temperatury:
Htr - współczynnik straty mocy cieplnej przez przenikanie
Hve - współczynnik straty mocy cieplnej przez wentylację
1.2. Bilans (uproszczony) kotła
Oznaczenia:
.
E ch
.
E str
.
I w,1
.
I w,2
- strumień energii chemicznej paliwa
- strumień strat ciepła źródła
- strumień energii nośnika ciepła doprowadzonego do źródła
- strumień energii nośnika ciepła wyprowadzanego od źródła
Równanie bilansu
Ed = Ew
.
+
I w,1
-
.
E str
E str
=
I w,2
=
E uż
E ch
=
E ch  E str
E ch
η źr,c
E ch
=
m
=
m
.
E ch
η źr,c
.
=
E ch
.
.
.
E uż
.
.
.
.
+
I w,2
-
I w,1
.
< 1
∙ cp ∙ ( tw,2 - tw,1 )
∙ cp ∙ ( tw,2 - tw,1 )
2.1. stan nieustalony
Ed = ΔEu
ΔEu = U2 - U1
ΔEu = m ∙ c ∙ ( t2 - t1 )
m
c
( t2 - t1 ) -
masa przegrody, [kg]
ciepło właściwe przegrody, [J/(kg K)]
przyrost temperatury przegrody, [K]
E d = m ∙ c ∙ ( t2 - t1 )