Lista zadań nr 10 do zajęć z matematyki – LS NE FiR
Elementy rachunku prawdopodobieństwa i statystyki
A1. Obliczyć prawdopodobieństwo zdarzeń A i B jeśli:
a) Prawdopodobieństwo zdarzenia A jest dwukrotnie większe niż prawdopodobieństwo zdarzenia
B, oraz dwukrotnie mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do B.
b) Zdarzenia A i B są równoprawdopodobne, zawsze zachodzi przynajmniej jedno z nich, a
prawdopodobieństwo zajścia zdarzenia A pod warunkiem zajścia zdarzenia B jest równe ¼.
A2. W wyniku pewnego egzaminu 10 studentów otrzymało ocenę 5.0, 15 ocenę 4.5, 30 ocenę 4.0, 27
ocenę 3.5, 21 osób ocenę 3.0. a) Ilu studentów nie otrzymało oceny pozytywnej, jeśli średnia
z egzaminu wynosiła 3.5? b) Obliczyć medianę, modalną, wariancję i odchylenie standardowe oraz
c) wyznaczyć i narysować dystrybuantę empiryczną dla powyższych danych.
A3. a) Znaleźć rozkład zmiennej losowej, której dystrybuanta określona jest wzorem F(x) = 0 dla x < 0,
F(x) = 0,3 dla x ∈ [0, 1), F(x) = 0,7 dla x ∈ [1, 2), F(x) = 1 dla x ≥ 2. b) Obliczyć wartość
oczekiwaną rozkładu, c) medianę i modalną, oraz d) wariancję i odchylenie standardowe.
A4. Zmienna losowa X ma rozkład Bernoulliego B(5; 0,2). a) Obliczyć P(X = 1), P(X = 3), P(X < 4),
P(X > 2). b) Obliczyć średnią i wariancję tego rozkładu.
A5. Zmienna losowa X ma rozkład Bernoulliego B(50; 0,1). Korzystając z możliwości przybliżenia
rozkładu Bernoulliego rozkładem Poissona obliczyć: a) P(X = 3), b) P(X = 5), c) P(X < 5),
d) P(2< X < 6), e) P(X > 4).
A6. Funkcja gęstości pewnego rozkładu dana jest wzorem f (x) = 0, dla x <0 i x ≥ 3; f (x) =
1
3
x dla x ∈
[0, 2), f (x) = 2 – x dla x ∈ [2, 3). a) Wyznaczyć dystrybuantę tego rozkładu. b) Obliczyć modalną
i medianę c) oraz wartość oczekiwaną i wariancję tego rozkładu.
2
3
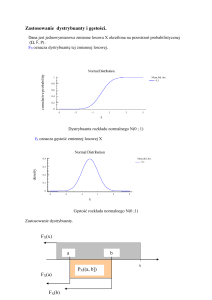
A7. Trzy spośród czterech zmiennych, których funkcje gęstości i dystrybuanty przedstawiono na
rysunkach poniżej, mają rozkład normalny. a) Oszacować wartość oczekiwaną i odchylenie
standardowe dla każdej z nich. b) Jaki rozkład ma czwarta zmienna?
1
0.8
0.6
0.4
0.2
-2
-1
1
2
3
1
2
3
1
0.8
0.6
0.4
0.2
-2
-1
B8. Liczba awarii w przeciągu godziny w pewnym zakładzie ma rozkład wykładniczy z parametrem
λ = 0,5. a) Jakie jest prawdopodobieństwo, że w losowo wybranej godzinie zdarzy się przynajmniej
jedna awaria w tym zakładzie? b) Ile średnio w ciągu godziny zdarza się awarii w tym zakładzie?
B9. Ciężar kurzych jaj zniesionych w pewnym gospodarstwie ma rozkład N(0,05 kg, 0,005 kg2).
a) Obliczyć prawdopodobieństwo, że 20 sztuk losowo wybranych jaj będzie ważyło razem więcej
niż 1,02 kg. b) Przy założeniu, że ciężar jaj ma rozkład normalny obliczyć prawdopodobieństwo, że
różnica między wagą dwóch jaj przekroczy 20 gramów?
B10. Mówimy, że zmienna losowa X ma efekt braku pamięci, jeśli P(X > x + x0| X > x0) = P(X > x).
Wykazać, że jeśli X jest zmienną losową o rozkładzie wykładniczym, to ma efekt braku pamięci.
●◘○●◘○●◘○●◘○●◘○●◘○●◘○
P(A) – prawdopodobieństwo zdarzenia A.
P(A) ≥ 0, P( ∅ ) = 0, P(Ώ) = 1, P(A ∪ B) = P(A) + P(B) – P(A ∩ B).
P(A | B) = P(A ∩ B) / P(B) – prawdopodobieństwo zdarzenia A pod warunkiem zdarzenia B.
Zdarzenia A i B są niezależne, jeśli P(A ∩ B) = P(A) P(B).
Zmienna losowa X ma rozkład dwumianowy (Bernoulliego, X~B(p, n)) jeśli P(X = k) =
gdzie 0 ≤ p < 1 – prawdopodobieństwo sukcesu, n – liczba prób, k ∈ {0, 1, …, n},
( )=
n
k
( )p (1− p)
n
k
k
n −k
,
n!
k !( n − k )! .
Zmienna losowa X ma rozkład Poissona z parametrem λ (X~P(λ)), jeśli P(X = k) = λk ! e − λ , gdzie
k ∈ {0, 1, 2,…).
Uwaga: Jeśli n jest duże (np. n > 50), p małe (p < 0,2), λ średnie (λ ∈ [0,1; 10)), wtedy rozkład
dwumianowy można przybliżać za pomocą rozkładu Poissona, tj. B(p, n) ≈ P(λ), gdzie λ ≈ np.
Zmienna losowa X (X > 0) ma rozkład wykładniczy z parametrem λ > 0 (X~Exp(λ)), jeśli
k
≤ = λ
∫
b
0
e −λx dx , dla b > 0.
Zmienna losowa X ma rozkład Gaussa (normalny) z parametrami µ i σ >0 (X~N( µ , σ )), jeśli
( ≤ ≤ ) =
1
2π σ
∫
b
a
e
−
( x−µ )2
2σ 2
dx .
() = ( < ) – dystrybuanta zmiennej losowej X.
Jeśli X jest zmienną losową o rozkładzie ciągłym to F(x) =
∫
x
-∞
f (t )dt , gdzie f jest funkcją gęstości
zmiennej losowej X. Inaczej: jeśli F(x) jest funkcją różniczkowalną względem x, to f (x) =
Średnia (wartość oczekiwana, przeciętna, nadzieja matematyczna) zmiennej X: EX =
d
dx
F(x).
∫ xdP(x) .
W przypadku, gdy X przyjmuje wartości w zbiorze {x1, x2 , ...} (czyli gdy X ma rozkład dyskretny) to
= ∑ ( = ). Jeśli X ma funkcję gęstości f (x) (X ma rozkład ciągły) to EX = ∫ xf ( x)dx .
Wariancja zmiennej losowej X: VarX = E(X - EX)2 = EX2 - (EX)2. EXk - moment rzędu k.
Odchylenie standardowe X: SDX = VarX .
X~B(p, n) ⇒ EX = np., VarX = np.(1 - p).
X~Exp(λ)⇒ EX = λ–1, VarX = λ–2.
X~P(λ) ⇒ EX = λ., VarX = λ .
X~ N( µ , σ ) ⇒ EX = µ , VarX = σ 2.
Twierdzenie (Nierówność Czebyszewa):
Jeśli X jest nieujemną zmienną losową o skończonej wartości oczekiwanej EX, to P(X ≥ ε)≤ EX ⁄ ε.
Jeśli natomiast X jest dowolną zmienną losową o skończonej wartości oczekiwanej i wariancji, to dla
dowolnej liczby ε >0 P(|X - EX| ≥ ε) ≤ VarX ⁄ ε2. Inaczej: P(|X - EX| ≥ k SDX) ≤ 1 ⁄ k2.
Ad. A1. b) P(A) = P(B); P(A ∪ B) = 1; P(A ∩ B) = ¼ P(B).
−x
Ad. B10. P(X > x) = 1 - F(x) = e λ . P(X > x + x0| X > x0) = e
−
( x − xo )
λ
xo
− λx
e =e .
λ