Zastosowanie dystrybuanty i gęstości.

Zastosowanie dystrybuanty i gęstości.
Dana jest jednowymiarowa zmienne losowa X określona na przestrzeń probabilistycznej
(Ώ, F, P) .
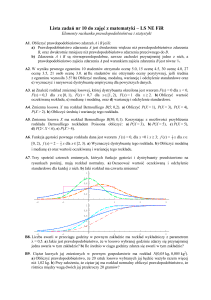
FX oznacza dystrybuantę tej zmiennej losowej.
cumulative probability
Normal Distribution
1
Mean,Std. dev.
0,1
0,8
0,6
0,4
0,2
0
-5
-3
-1
1
3
5
x
Dystrybuanta rozkładu normalnego N(0 ; 1)
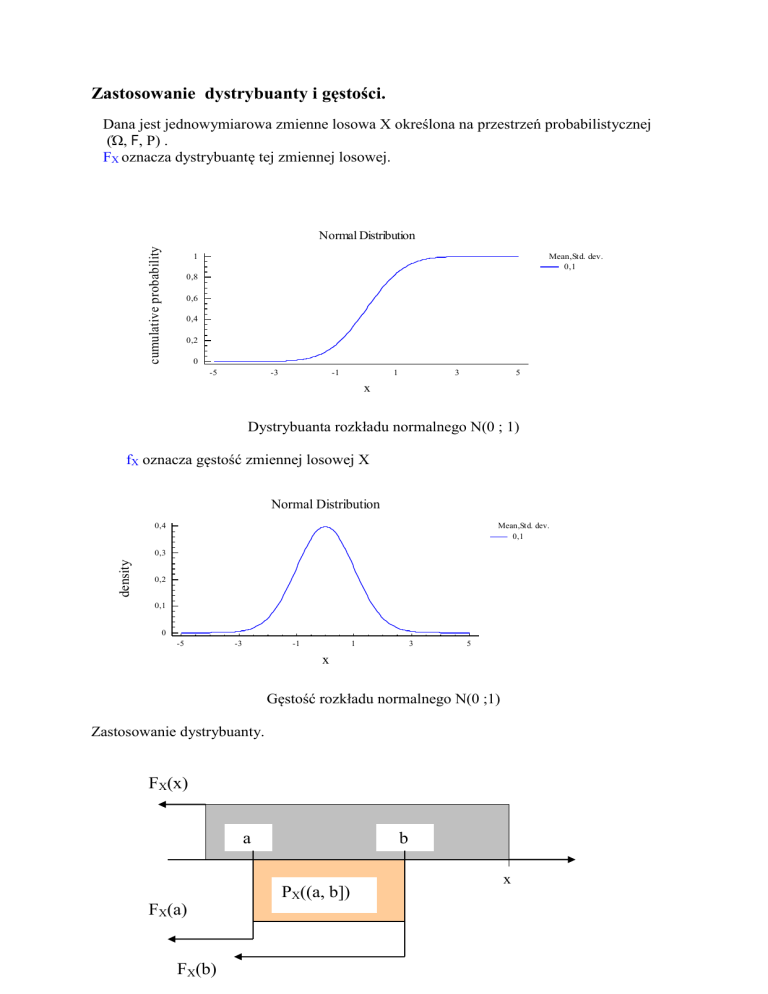
fX oznacza gęstość zmiennej losowej X
Normal Distribution
0,4
Mean,Std. dev.
0,1
density
0,3
0,2
0,1
0
-5
-3
-1
1
3
5
x
Gęstość rozkładu normalnego N(0 ;1)
Zastosowanie dystrybuanty.
FX(x)
a
b
PX((a, b])
FX(a)
FX(b)
x
cumulative probability
Normal Distribution
1
Mean,Std. dev.
0,1
0,8
0,6
PX((a,b])
0,4
0,2
0
-5
-3
a-1
b1
3
5
x
PX((a, b]) = P(X  (a, b]) = FX (b) - FX (a)
PX((a, b]) = P(X (a, b]) = FX (b) - FX (a) =
b
f
a
X
(t )dt
Distribution
PX((a, b]) =Normal
P(X 
(a, b]) =
0,4
b
f
X
(t )dt
Mean,Std. dev.
0,1
a
density
0,3
0,2
0,1
0
-5
-3
-1
1
3
5
x
Kwantyle.
Definicja.
Kwantylem rzędu  jednowymiarowej zmiennej losowej X nazywa się taką liczbę q ,że
FX (q- )    FX (q)
cumulative probability
Normal Distribution

1
Mean,Std. dev.
0,1
0,8
0,6
FX(x)
0,4
0,2
0
-5
-3
-1
x
1
x
q
3
5
q

f
X
(t )dt

Standaryzacja zmiennej losowej X.
Przekształcenie
U
X  EX
X
przekształca zmienną losową X w zmienną losową U taką, że:
- jej wartość oczekiwana E(U) =0,
- jej odchylenie standardowe 𝜎𝑈 = 1.
W szczególności zmienna losowa o rozkładzie normalnym N(m;σ) poprzez przekształcenie
U
X m

na zmienną losową o rozkładzie normalnym N(0;1).
Zadanie.
Zużycie paliwa na przejechanie przez pojazd 100km ma rozkład normalny N(10;2). Co
oznacza, że średnie zużycie paliwa wynosi 10 l/100 km średnim odchyleniem 2 l.
Wyznaczyć Wpisz tutaj równanie.prawdopodobieństwo tego, że zużycie paliwa na
przejechanie 100 km będzie się wahało pomiędzy 8 a 12 litrów paliwa,
Rozwiązanie
Oznaczając przez X losową ilość paliwa zużytą na przejechanie 100 km.
Z treści zadania wynika, że zmienna losowa X ma rozkład normalny N(10;2).
P(8<X≤12) =
Wykorzystując przekształcenie standaryzacyjne
= 𝑃(
8−10
2
<
𝑋−10
2
≤
12−10
2
) = 𝑃(−1 < 𝑈 ≤ 1) =
Odczytując odpowiednie wartości z tablic dystrybuanty rozkładu normalnego N(0;1)
𝐹𝑈 (1) − 𝐹𝑈 (−1) = 0,84 - 0,16 =0,68
Twierdzenie Moivre’a - Laplace’a
Jeżeli zmienna losowa X ma rozkład dwumianowy B(n;p), to
lim P(
X  np
n 
npq
 x )  FU ( x )
Zadanie.
W natarciu bierze udział 300 czołgów. Prawdopodobieństwo tego, że nieuszkodzony czołg
dotrze do linii przełamania wynosi p=0,4. Natarcie będzie udane, jeżeli przynajmniej 100
czołgów dotrze do linii przełamania.
Wyznaczyć prawdopodobieństwo tego, że natarcie czołgów zakończy się sukcesem.
Rozwiązanie
Oznaczając przez X zmienną losową ilości nieuszkodzonych czołgów na linii przełamania.
Zmienna X ma rozkład dwumianowy B(300;0,4). Natarcie będzie udane, jeżeli X ≥ 100.
P(X ≥ 100) =
Wykorzystując przekształcenie standaryzacyjne
=𝑃(
𝑋−300∙0,4
√300∙0,4∙0,6
≥
100−120
√72
)=
Z twierdzenia Moivre’a - Laplace’a
= 𝑃(𝑈 ≥ −2,36) = 1 − 𝐹𝑈 (−2,36) = 1 − 0,009 = 0,991