ZEROWA ZASADA TERMODYNAMIKI

1
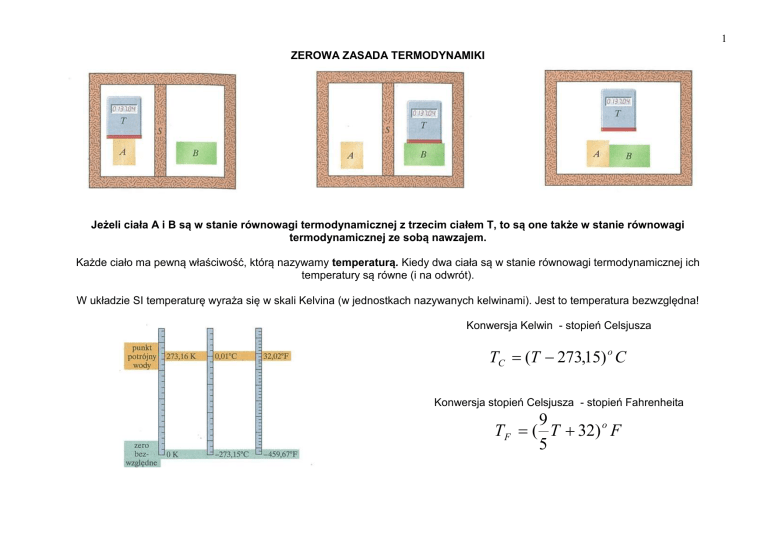
ZEROWA ZASADA TERMODYNAMIKI
Jeżeli ciała A i B są w stanie równowagi termodynamicznej z trzecim ciałem T, to są one także w stanie równowagi
termodynamicznej ze sobą nawzajem.
Każde ciało ma pewną właściwość, którą nazywamy temperaturą. Kiedy dwa ciała są w stanie równowagi termodynamicznej ich
temperatury są równe (i na odwrót).
W układzie SI temperaturę wyraża się w skali Kelvina (w jednostkach nazywanych kelwinami). Jest to temperatura bezwzględna!
Konwersja Kelwin - stopień Celsjusza
TC  (T  273,15) o C
Konwersja stopień Celsjusza - stopień Fahrenheita
9
TF  ( T  32) o F
5
2
ROZSZERZALNOŚĆ CIEPLNA
Rozszerzalność liniowa
L  LT
Substancja
Lód
Ołów
Stal
Szkło
Kwarc
[10-6/ºC]
51
29
11
9
0,5
Rozszerzalność objętościowa
V  VT
  3
3
Temperatura i ciepło
Ciepło jest energią przekazywaną między układem a jego otoczeniem na skutek istniejącej między nimi różnicy temperatury.
Zwyczajową jednostką ciepła jest kaloria - ilość ciepła potrzebna do podniesienia temperatury 1g wody od 14,5 do 15,5ºC
W układzie SI jednostką ciepła jest dżul
1 cal = 4,1860 J
Pochłanianie ciepła prze ciała stałe i ciecze
Pojemność cieplna:
C
Q
; Q
T
4
Ciepło właściwe:
c
Q
; Q
mT
c  
J 

 kg  K 
Ciepło przemiany:
c przem 
Q
; Q
m
c    kgJ 
przem


Przykład: Ile ciepła musi pobrać lód o masie m= 1000g i temperaturze -20ºC aby zamienił sie w wodę o temperaturze 20ºC
cw = 1cal/gK, cl = 0,5 cal/gK, cTop = 80 cal/g
PRACA W GAZACH
dW 
W
VK
 pdV
V0
5
PIERWSZA ZASADA TERMODYNAMIKI
Fakt doświadczalny: Q - W = const
We wszystkich powyższych procesach!!
U  U K  U 0  Q  W
6
Zmiana energii wewnętrznej układu jest równa różnicy ciepła dostarczonego do układu i pracy wykonanej przez układ
dU  dQ  dW
Przypadki szczególne:
1. Przemiana adiabatyczna
U  W
2. Przemiana izochoryczna (V = const)
U  Q
3. Proces cykliczny
Q W
4. Rozprężanie swobodne
U  0
7
MECHANIZM PRZEKAZYWANIA CIEPŁA
1. Przewodnicwo cieplne
Strumień ciepła
Q
t
T
Pprzew  kS
L
Pprzew 
k - przewodność cieplna właściwa
Opór cieplny:
R
Pprzew 
2. Konwekcja
3. Promieniowanie
Pprom   ST 4
L
kS
8
KINETYCZNA TEORIA GAZÓW
Kiedy rozpatrujemy układy cząsteczek posługujemy się wielkością próbki wyrażoną w molach. Mol jest miarą ilości substancji.
Jeden mol to liczba atomów (lub cząsteczek) odpowiadających liczbie atomów w próbce węgla (C12) o masie 12 g.
Liczba tych atomów (cząsteczek) jest równa liczbie Avogadra NA = 6,0210-12 mol-1.
Liczba moli substancji w próbce jest równa ilorazowi liczby cząstek N w próbce i liczby Avogadra.
n
Masa jednego mola jest równa iloczynowi masy pojedynczej cząstki i liczby Avogadra.

Znając masę molową można wyznaczyć liczbę moli w próbce jeżeli znamy masę próbki.
n
9
Gazy doskonałe
Gaz doskonały – zwany gazem idealnym jest to abstrakcyjny, matematyczny model gazu, spełniający następujące warunki:
1.
2.
3.
4.
brak oddziaływań międzycząsteczkowych
objętość cząsteczek jest znikoma w stosunku do objętości gazu
zderzenia cząsteczek są doskonale sprężyste
cząsteczki znajdują się w ciągłym chaotycznym ruchu
W praktyce gazy rzeczywiste zachowują się w przybliżeniu jak gaz doskonały pod dostatecznie niskim ciśnieniem, czyli kiedy ich gęstość
jest dostatecznie mała
Parametry stanu gazu doskonałego powiązane są wzajemnie równaniem stanu gazu doskonałego.
pV  nRT
równanie stanu gazu doskonałego (Clapeyrona)
Symbol R oznacza pewną stałą, nazywaną stałą gazową - R  8,31 J / mol  K 
Równanie stanu gazu można również zapisać wykorzystując zamiast liczby moli liczbę cząsteczek gazu.
pV  NkT
inna postać równania stanu gazu doskonałego
Oczywiście tożsamość tych równań wymaga aby:
Symbol k oznacza stałą Boltzmanna - k  1,38 1023 J / K
10
MOLEKULARNE ŹRÓDŁO CIŚNIENIA GAZU
Zmiana pędu cząstki przy zderzeniu ze ścianką
naczynia:
pX 
szybkość przekazu pędu:
p X

t
Ciśnienie wywierane na ściankę naczynia
p
Dla dowolnej cząstki v 2 
11
ale z uwagi na olbrzymia liczbę cząstek gazu, które poruszają się w przypadkowych kierunkach można przyjąć że średnie wartości
1
kwadratów składowych prędkości są sobie równe a więc: v x2  v 2
3
czyli ostatecznie ciśnienie możemy zapisać w postaci :
często dla wyrażenia
v 
2
śr
wprowadza się oznaczenie vśr.kw. - nazywa się je prędkością średnią kwadratową.
Wtedy zależność opisując ciśnienie przyjmie postać: p 
n  vśr2 .kw
3V
Korzystając z równania Clapeyrona możemy wyznaczyć prędkość średnią kwadratową:
vśr.kw. 
3RT

prędkość średnia kwadratowa
Energia kinetyczna ruchu cząstek
W dowolnej chwili czasu energia kinetyczna cząstki ma postać:
Dla własności gazu złożonego z ogromnej liczby cząstek istotne znaczenie ma średnia energia cząstek.
12
EK 
Średnia energia kinetyczna
Ek .śr . 
3
kT
2
W danej temperaturze T wszystkie cząsteczki gazu doskonałego – niezależnie od swojej masy – mają taką sama energie kinetyczną ruchu
postępowego, równą 3/2 kT. Mierząc temperaturę gazu wyznaczamy jednocześnie średnią energię kinetyczną ruchu postępowego jego
cząsteczek.
Średnia droga swobodna
Poruszająca się cząsteczka gazu zderza się wzdłuż swojego toru z innymi cząstkami.
Próba pełnego opisu takiego ruchu jest w praktyce skazana na niepowodzenie.
Ruch cząstek gazu opisuje się na ogół jedynie statystycznie, jednym z użytecznych parametrów
takiego opisu jest średnia droga swobodna .
13
Parametr  zgodnie ze swoją nazwą mówi nam jaką drogę pokonuje cząstka średnio między kolejnymi zderzeniami.
Spróbujmy wyznaczyć ten parametr przyjmując pewne
założenia:
1. pewna wybrana cząstka porusza się z prędkośćią v
a pozostałe cząstki pozostają w spoczynku
2. cząstki są kulami o średnicy d – zderzenie nastąpi
jeżeli odległość między środkami dwu cząstek
wyniesie d.
 = (droga cząstki w czasie t)/(liczba zderzeń w czasie t)

W rzeczywistości ponieważ wszystkie cząstki się poruszają co powoduje że zależność ta wymaga ilościowej modyfikacji.

1
2 d 2 N / V
średnia droga swobodna
14
Rozkład prędkości cząstek
Jako miarę prędkości cząstek gazu w określonej temperaturze przyjęliśmy wcześniej prędkość średnią kwadratową. Jest to jednak pewna
konkretna wartość nie mówiąca nic o tym jaka część cząstek ma prędkość większą, a jaka mniejszą od tej konkretnie prędkości.
Aby w pełni scharakteryzować prędkości cząsteczek w gazie można wykorzystać funkcję rozkładu prawdopodobieństwa określającą jakie
jest prawdopodobieństwo znalezienia cząstki z pewnego określonego przedziału prędkości.
Ponieważ prawdopodobieństwo tego że cząstka ma jakąkolwiek prędkość z przedziału 0,  jest dokładnie równe jedności można zapisać.

 Pvdv  1
0
Aby policzyć ułamek cząstek zawartych w przedziale prędkości v1,v2 trzeba wyznaczyć wartość całki
V2
 Pv dv
V1
15
Rozkład prędkości cząsteczek
gazu po raz pierwszy wyznaczył
James Clark Maxwell, wyraża
się on wzorem:
 
Pv   4 
 2 RT



3/ 2
v 2e v
2
/ 2 RT
Znając rozkład prędkości cząsteczek gazu możemy wyznaczyć:
1. Średnią prędkość cząsteczek gazu
Jeżeli znana jest funkcja rozkładu prawdopodobieństwa f(x) dla pewnej zmiennej x to aby policzyć wartość średnią tej zmiennej musimy
wyznaczyć wartość wyrażenia:
x   x  f x dx
D
W przypadku średniej prędkości otrzymamy:
v 
vśr 
8RT

średnia prędkość cząsteczek gazu
16
2. Prędkość średnią kwadratową
v2 
vśr.kw. 
3RT

średnia prędkość kwadratowa
3. Prędkość najbardziej prawdopodobną
Jest to prędkość dla której funkcja rozkładu prawdopodobieństwa osiąga wartość maksymalną.
Można ją wyznaczyć korzystając z warunku że w maksimum funkcji jej pochodna osiąga wartość maksymalną.
dP
0
dv
vp 
2 RT

prędkość najbardziej prawdopodobna
17
Ciepło molowe gazów doskonałych
Energia wewnętrzna
Energia wewnętrzna gazu doskonałego jest po prostu sumą energii kinetycznych wszystkich jego cząstek związanych z ich ruchem
postępowym.
EW   EKi
i
Zamiast liczyć tę sumę, możemy skorzystać ze średniej energii kinetycznej dla każdej z cząstek, wtedy:
EW  NCZ  EK
EW 
3
nRT
2
energia wewnętrzna jednego mola gazu doskonałego
18
Molowe ciepło właściwe przy stałej objętości
Jeżeli nie zmienia się objętość gazu to nie wykonuje on żadnej pracy.
W 0
Zgodnie z pierwszą zasadą termodynamiki
Q
ale ogólnie ciepło przemiany możemy zapisać
Q
19
Ciepło molowe przy stałej objętości gazu
doskonałego
CV 
3
R
2
Zmiana energii wewnętrznej gazu
doskonałego zamkniętego w zbiorniku
zależy tylko od zmiany temperatury gazu,
nie zależy natomiast od typu procesu w
którym nastąpiła zmiana temperatury
EW  nCV T
Molowe ciepło właściwe przy stałym ciśnieniu
W   dW 
VK
 p(v)dv
VP
20
W warunkach stałego ciśnienia:
W  pV
ale
pV  nRT
Praca wykonana przez gaz podczas rozprężania pod stałym ciśnieniem
(izobarycznie)
W  nRT
Ogólnie ciepło tej przemiany możemy zapisać w postaci:
Q
ale zgodnie I zasadą termodynamiki
Wynika z tego następująca zależność:
CP  CV  R
21
Molowe ciepła właściwe gazów wieloatomowych – stopnie swobody
f = 3 (x,y,z)
f=5
f=6
Zasada ekwipartycji energii - Każdy rodzaj cząstek charakteryzuje pewna liczba stopni swobody f , które dają cząsteczce niezależne
1
1
sposoby magazynowania energii. Na każdy stopień swobody przypada średnio energia równa kT na cząsteczkę (lub RT w przeliczeniu
2
2
na mol)
Uogólniając można zapisać ciepło molowe przy stałej objętości dla gazów jedno-, dwu- i wieloatomowych w postaci
f 
CV    R
2
22
Ciepło molowe gazów rzeczywistych
Zależność ciepła molowego
od temperatury dla
dwuatomowego wodoru
PRZEMIANA ADIABTYCZNA
23
pV   const; 

p1V1  p2V2
 CP CV

 1
TV  1  const ; T1V1
Wyprowadzenie:
 T2V2
 1
24
ENTROPIA
Przemiana nieodwracalna w układzie zamkniętym powoduje zawsze w układzie zamkniętym wzrost entropii układu - NIGDY jej spadek
Entropię można charakteryzować na dwa sposoby:
1) poprzez ilość dostarczonego ciepła i temperaturę w jakiej było ono dostarczane - ściśle rzecz biorąc charakteryzujemy wtedy zmiany
entropii.
2) poprzez wyznaczenie możliwych kombinacji ułożenia atomów lub cząsteczek w układzie.
K
dQ
dt
P
S  S K  S P  
25
Aby wyznaczyć zmianę entropii w przemianie nieodwracalnej zachodzącej w układzie zamkniętym należy zastąpić te przemianę dowolną
przemianą odwracalną o takim samym stanie początkowym i końcowym.
S  S izoterm 
26
ENTROPIA JAKO FUNKCJA STANU
dU  dQ  dW
S  nR ln
VK
T
 nCV ln K
VP
TP
DRUGA ZASADA TERMODYNAMIKI
W układzie zamkniętym ciepło może przepływać między elementami układu, nie może go jednak opuszczać ani być do niego dostarczane.
Dla układu gaz - rezerwuar ciepła
dQG  dQR
Dla przemiany izotermicznej otrzymamy:
S  0
27
II ZT: Entropia układu zamkniętego wzrasta w przemianach nieodwracalnych i nie zmienia się w przemianach odwracalnych. ENTROPIA
NIGDY NIE MALEJE.
S  0
SILNIK CARNOTA
W silniku idealnym wszystkie procesy są odwracalne i nie ma strat spowodowanych turbulencją czy tarciem.
28
Praca w jednym cyklu
E  Q  W W 
S  SG  SZ 
SPRAWNOŚĆ SILNIKA CARNOTA:

W
energia uzyskana

energia dostarczona QG
C 
C 
TG  TZ
- sprawność silnika Carnota
TG
Nie jest możliwy żaden ciąg przemian, którego jedynym skutkiem byłoby pobranie
ciepła i całkowita zamiana go w pracę.
Nie jest możliwe skonstruowanie perpetuum mobile drugiego rodzaju
29
SILNIK STIRLINGA
Silnik Stirlinga – silnik cieplny, który przetwarza energię cieplną w energię mechaniczną, jednak bez
procesu wewnętrznego spalania paliwa, a
na skutek dostarczania ciepła z zewnątrz,
dzięki czemu możliwe jest zasilanie go
ciepłem z dowolnego źródła. Źródłem ciepła
może być w szczególności proces spalania
jakiegoś paliwa, ale nie jest to konieczne.
SILNIKI SPALINOWE
DIESEL
OTTO
30
CHŁODZIARKI
W idealnej chłodziarce wszystkie procesy są odwracalne i nie ma rozpraszania energii.
K
energia odebrana
- współczynnik wydajność chłodziarki
energia dostarczon a
Dla chłodziarki Carnota
KC 
KC 
S  
QZ
TZ

TZ
TG  TZ
QG
TG
Gdyby tyle samo ciepła pobierać co oddawać to
S 
Ale entropia nie może maleć !!!
Nie można przeprowadzić ciągu procesów, którego jedynym rezultatem jest oddanie energii w postaci ciepła przez ciało chłodniejsze ciału
cieplejszemu (IIZT)
31
SPRAWNOŚĆ SILNIKÓW RZECZYWISTYCH
Załóżmy, że można skonstruować silnik o sprawności większej niż sprawność silnika Carnota.
 X  C
Można by go wykorzystać do napędu chłodziarki Carnota.
Z definicji sprawności:
W
QGX

W
QGC
Żaden silnik rzeczywisty nie może mieć sprawności większej niż silnik Carnota współpracujący ze zbiornikami cieplnymi o tych samych
temperaturach.
32
STATYSTYCZNE PODEJŚCIE DO ENTROPII
Wszystkie mikrostany są równoważne.
Całkowita liczba mikrostanów w układzie opisana jest zależnośćcią:
L
L  N!
Różne konfiguracje NIE są równoważne ponieważ możne je
utworzyć z RÓŻNEJ liczby mikrostanów
KROTNOŚĆ KONFIGURACJI
Rozważmy 6 cząstek:
Konfiguracja
Symbol
n1
Liczba mikrostanów w danej konfiguracji
n2
Entropia [10-23 J/K]
33
Konfiguracja z największą liczbą mikrostanów jest konfiguracją
najbardziej prawdopodobną.
Prawdopodobieństwo bardzo szybko malej wraz ze wzrostem
nierównomierności podziału cząstek pomiędzy dwie części naczynia.
Wzór Boltzmanna na entropię:
S  k ln W
Wyznaczenie W jest dość trudne - jest to ogromna liczba
Wygodnie jest skorzystać z przybliżonego wzoru na logarytm z silni:
ln N! N ln N   N
- wzór Stirlinga