WARUNKI RÓWNOWAGI UKŁADU TERMODYNAMICZNEGO

WARUNKI RÓWNOWAGI UKŁADU
TERMODYNAMICZNEGO


Proces termodynamiczny zachodzi dopóty, dopóki układ nie
osiągnie stanu równowagi. W stanie równowagi odpowiedni
potencjał termodynamiczny układu osiąga minimum, podczas
gdy entropia układu i otoczenia osiąga maksimum.
W szczególności:


Kiedy entropia (S) i "zewnętrzne parametry" (np. objętość) zamkniętego
układu termodynamicznego są stałymi parametrami przemiany, energia
wewnętrzna (U) maleje i osiąga minimalną wartość w punkcie
równowagi. Wynika to z pierwszej i drugiej zasady termodynamiki i jest
nazwane zasadą minimum energii.
Kiedy temperatura (T) i zewnętrzne parametry zamkniętego układu
termodynamicznego są stałe, energia swobodna Helmholtza (F) maleje i
osiąga minimalną wartość w punkcie równowagi.
WARUNKI RÓWNOWAGI UKŁADU
TERMODYNAMICZNEGO
 Kiedy
ciśnienie (p) i zewnętrzne parametry
zamkniętego układu termodynamicznego są stałe,
entalpia (H) maleje i osiąga minimalną wartość w
punkcie równowagi.
 Kiedy temperatura (T), ciśnienie (p) i zewnętrzne
parametry zamkniętego układu
termodynamicznego są stałe, entalpia swobodna
Gibbsa (G ) maleje i osiąga minimalną wartość w
punkcie równowagi.
KONIEC WYKŁADU I
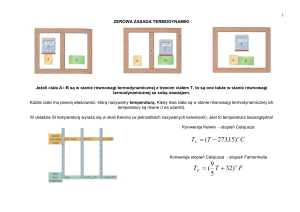
TEMPERATURA A ENERGIA CIAŁA

Przez układy termodynamiczne będziemy
rozumieć makroskopowe ciała, które mogą
wymieniać się energią zarówno między sobą jak
i również z ośrodkiem zewnętrznym, czyli
otoczeniem.
TEMPERATURA
Temperatura układu termodynamicznego
jest miarą ruchu cieplnego jego cząstek
(cząsteczek, atomów, jonów).
 Jeżeli układ termodynamiczny pozostaje w
stanie równowagi, to średnia energia
kinetyczna ruchu cieplnego jego cząstek jest
wprost proporcjonalna do termodynamicznej
temperatury układu:

~
E  kT
k – stała Boltzmana k = 1,38 10-23 , JK-1,
T - temperatura (bezwzględna) ciała.
ROZKŁAD PRĘDKOŚCI CZĄSTEK
W OBJĘTOŚCI V
Ilość cząstek uderzających
w ściankę S można wyliczyć jako:
n
S
dV
 ;
V
dV  lS  vtS;

N
6
Zmiana pędu n cząstek:
p  n  2mv  F  t  F 
2mvn
t
F 2mvn
vN
2mv 2 N
P 
 2mvn 

S
tS
n6V
6V
l
Po podstawieniu Ek = mv2/2 otrzymujemy
RÓWNANIE STANU GAZU DLA N CZĄSTEK
Po podstawieniu:
Otrzymamy:
I dalej po podstawieniach:
nm – liczba moli gazu;
lub
A- liczba Avogadro,
pV
 nm R  const
T
R - stała gazowa
ROZKŁAD ENERGII CZĄSTEK
 Er 
Pr  C exp  

 kT 
 Er 
r Pr  1 C r exp   kT   1
 E 
exp   r 
1
 kT 
C
Pr 
 Er 
 Er 
r exp   kT 
r exp   kT 
s  k ln 
ROZKŁAD ENERGII CZĄSTEK
OZIĘBIANIE WEWNĘTRZNE

Poprzez zmianę, w warunkach izentropowych, jednego
z termodynamicznych parametrów intensywnych:
ciśnienia,
 natężenia pola magnetycznego
oraz utrzymanie wysokiego stopnia uporządkowania ciała przy
zmianie jego energii (patrz rys. rozkład energii cząstek)
s = k ln Ω = const

– oznacza to, że w procesie izentropowym nie zmienia się liczba
stanów, zmienia się natomiast ich szerokość – obniżeniu ulega
średnia energia ruchów cieplnych (patrz rys.)
OZIĘBIANIE ZEWNĘTRZNE
Poprzez kontakt cieplny ciała o temperaturze
wyższej z ciałem o temperaturze niższej, a więc
o niższej energii ruchów cieplnych cząstek.
 Na mocy zerowej zasady termodynamiki
nastąpi wtedy wyrównanie temperatur obu ciał i
przepływ ciepła od ciała o temperaturze wyższej
do ciała o temperaturze niższej.
 Taki sposób obniżania temperatury ciała
nazwiemy oziębianiem zewnętrznym.

OZIĘBIANIE ZEWNĘTRZNE I WEWNĘTRZNE
KONIEC WYKŁADU II
UOGÓLNIONY PROCES OZIĘBIANIA
WEWNĘTRZNEGO CIAŁA

Obniżenie entropii ciała w procesie izotermicznym
jest możliwe tylko wtedy, gdy funkcja ta zależy od
dwóch parametrów: temperatury T oraz pewnego
parametru stanu X o charakterze uogólnionej siły.
S  S (T , X )

W przypadku gazów parametr X jest ciśnieniem,
magnetyków - natężeniem pola magnetycznego,
dielektryków - natężeniem pola elektrycznego
UOGÓLNIONY PROCES OZIĘBIANIA
WEWNĘTRZNEGO CIAŁA

Uogólniona siła X musi być skojarzona z
przesunięciem Y, tak aby elementarna praca
wykonana nad ciałem wynosiła:
dW  XdY
dW  Fdr 
UOGÓLNIONY PROCES OZIĘBIANIA
WEWNĘTRZNEGO CIAŁA
UOGÓLNIONY PROCES OZIĘBIANIA W UKŁADZIE
TS.
Y2
W   XdY
Y1
Q  TA ( S A  S B )
dU  TdS  XdY
lub dH  TdS  YdX
gdzie H jest entalpią równą H  U  XY
S  S (T , X )
 S 
 S 
dS    dT    dX  0
 T  X
 X T
UOGÓLNIONY PROCES OZIĘBIANIA


Różniczkowy efekt
analizowanego procesu μs
jest równy:
gdzie cX jest ciepłem
właściwym ciała przy stałej
wartości parametru X
 S 


X T
 S 

s  
 
 S 
 X  S


 T  X
cX
 S 

 
 T  X T
UOGÓLNIONY PROCES OZIĘBIANIA

Zatem otrzymujemy:
 S 
T

 T 
 dX T
S  


cX
 dX  S

Zauważmy, że aby μs było różne od zera
konieczne jest, aby przy temperaturze T entropia
S zależała od wielkości X.
UOGÓLNIONY PROCES OZIĘBIANIA
Pochodną
 S 


 X T
wyznaczymy korzystając z różniczki entalpii
swobodnej F:
F = H − TS ,
stąd po zróżniczkowaniu otrzymujemy dF = −YdX − SdT
Korzystając z własności, że drugie pochodne są sobie
równe:
UOGÓLNIONY PROCES OZIĘBIANIA

Ostatecznie otrzymujemy ogólne wyrażenie
określające różniczkowy efekt obniżenia
temperatury w izentropowym procesie wykonania
pracy przez uogólnioną siłę X na uogólnionej
drodze Y:
 Y 
T

T  X
 dT 

S  
 
cX
 dX  S
WARUNKI POTRZEBNE DO OBNIŻENIA
TEMPERATURY
1.
Substancja dla której S = S(T, X)

2.
3.
4.
X ma charakter uogólnionej siły, np. ciśnienia lub natężenia pola
magnetycznego.
Obniżyć entropię w warunkach izotermicznych
Wykonać pracę z równoczesnym oddaniem ciepła do
otoczenia. (Przykładem takiego procesu jest izotermiczne
sprężenie gazu.)

WARUNKI POTRZEBNE DO OBNIŻENIA
TEMPERATURY
4.
Zrealizować przemianę, w której uogólniona siła wróci do swej
pierwotnej wartości, natomiast entropia ciała pozostanie
niska. W przemianie tej nastąpi obniżenie temperatury ciała z
tego powodu, że będzie miało miejsce jakościowe
przeobrażenie się entropii ciała. Obniżeniu ulegnie ta jej
część, która jest związana z temperaturą, wzrośnie natomiast
część określona przez uogólnioną siłę X.
ROZPRĘŻANIE IZENTROPOWE Z WYKONANIEM
PRACY ZEWNĘTRZNEJ.





Adiabatyczne i izentropowe rozprężenie gazu jest możliwe pod
warunkiem, że w gazie nie mają miejsca zjawiska
nieodwracalne, np. wewnętrznego tarcia.
Aby spełnić warunek s = const należy całą osiągalną energię
sprężonego gazu odebrać w postaci pracy zewnętrznej.
Praca musi zostać w całości wykonana nad obiektem
odizolowanym termodynamicznie od rozprężanego gazu.
W efekcie następują największe z możliwych spadki energii
wewnętrznej gazu oraz jego entalpii.
Spadek temperatury jest maksymalny i większy niż
obserwowany w innych procesach.
ROZPRĘŻANIE IZENTROPOWE Z WYKONANIEM
PRACY ZEWNĘTRZNEJ.

h1 2 '
h1 2
  współczynnik sprawności
w  (u1  p1v1 )  (u 2  p2 v2 )  h1  h2
w  zewnętrzna praca użyteczna
u1  energia wewn. gazu na wlocie
p1 v1  praca napełniani a
u 2  energia wewn. gazu na wylocie
p2 v2  praca opróżniania
ROZPRĘŻANIE IZENTROPOWE Z WYKONANIEM
PRACY ZEWNĘTRZNEJ.

Spadek temperatury gazu w procesie
izentropowego rozprężania może zostać
wyznaczony przez wyrażenie entropii jako funkcji
ciśnienia i temperatury S = S(p,T ), a następnie
przyrównanie do zera jej różniczki zupełnej.
 S 
 S 
dS  
 dT    dp  0
 T  p
 p T
ROZPRĘŻANIE IZENTROPOWE Z WYKONANIEM
PRACY ZEWNĘTRZNEJ.

Po przekształceniach otrzymujemy:
 dT 
 s   
 dp  S
 S 
 
p T


 S 


 T  p
 S 
 v 
Po podstawien iu :    
 oraz
 T  p
 p T
 v 
T

 dT 
 T  p Tv
 
Otrzymujemy :  s  

,
cp
cp
 dp  S
cp
 S 

 
 T  p T
1  v 
  
v  T  p
ROZPRĘŻANIE IZENTROPOWE Z WYKONANIEM
PRACY ZEWNĘTRZNEJ.

Z równania wynika, że zarówno dla gazu doskonałego
jak i dla gazów rzeczywistych współczynnik μs ma
wartość dodatnią, co oznacza, że spadkowi ciśnienia
gazu w procesie izentropowego rozprężania zawsze
towarzyszy spadek temperatury.
 dT 
 s   
 dp  S
 v 
T

 T  p Tv


cp
cp
ROZPRĘŻANIE IZENTROPOWE Z WYKONANIEM
PRACY ZEWNĘTRZNEJ

Po podstawieniu do powyższego równania - równania
stanu gazu doskonałego otrzymuje się:
 dT 
 1 T

   s 
 p
 dp  S
po scałkowaniu :
T2  p2 
  
T1  p1 
 1

ROZPRĘŻANIE IZENTROPOWE Z WYKONANIEM
PRACY ZEWNĘTRZNEJ

Schemat rozprężarki
tłokowej:

1- uszczelnienie, 2 tłok, 3 - cylinder, 4 –
zawory, 5 - popychacz
zaworów, 6 - układ
sterowania zaworami, 7
- mechanizm korbowy, 8
- hamulec (układ
pochłaniający energię
mechaniczną)
KONIEC WYKŁADU III
METODY UZYSKIWANIA NISKICH TEMPERATUR
DŁAWIENIE IZENTALPOWE
Dławienie – proces w którym gaz rozpręża się
adiabatycznie w układzie otwartym, bez
wykonania pracy zewnętrznej oraz bez zmiany
prędkości ani istotnej zmiany wysokości.
 Dławienie gazu może odbywać się w trakcie
jego przepływu przez porowatą zatyczkę, dyszą,
kapilarę czy zawór dławiący.

DŁAWIENIE IZOENERGETYCZNE
DŁAWIENIE IZENTALPOWE
DŁAWIENIE IZENTALPOWE

Bilans energii układu otwartego możemy zapisać

gdzie: q - ciepło, h - entalpia, w - prędkość, z wysokość, l – praca
W procesie adiabatycznego dławienia zarówno
ciepło q jak i praca przemiany - l są równe zero, a
zmiany prędkości gazu w oraz jego położenia z są
pomijalne, więc:

PRZEBIEG PROCESU DŁAWIENIA NA WYKRESIE
T-S
dh = 0
DŁAWIENIE IZENTALPOWE

Po przekształceniu drugiej zasady termodynamiki
 dh 
 ds 
dh  Tds  vdp do postaci    T    v
 dp T
 dp T
i po podstawieniu równania M axwella
 ds   dv 
   

 dp T  dT  p
otrzymujemy :
 dT 
 h   
 dp  h
 dv 
T
 v
 dT  p

cp
DŁAWIENIE IZENTALPOWE

Dla gazu idealnego z równania Clapeyrona:
pv  RT
R v

p T
RT
v
p
R v
 v 

  
 T  p p T
Różniczkowy współczynnik dławienia
 dT 
 h   
 dp  h
 dv 
T
 v T v v
 dT  p

 T
0
cp
cp
DŁAWIENIE IZENTALPOWE



Taka wartość μh wynika z faktu, że między cząstkami
gazu idealnego nie występują siły wzajemnego
oddziaływania.
W procesie dławienia izentalpowego gaz nie wykonuje
pracy zewnętrznej.
Jeżeli między cząstkami gazu nie występują
oddziaływania, to zwiększenie średniej odległości
pomiędzy nimi nie wymaga wykonania pracy kosztem
energii cieplnej cząstek E ≈ kT , gdzie k jest stałą
Boltzmanna. W efekcie temperatura gazu T pozostaje
niezmieniona.
DŁAWIENIE IZENTALPOWE


Dla gazów rzeczywistych
istnieją oddziaływania
pomiędzy cząsteczkami
Energię potencjalną tych
oddziaływań opisuje
potencjał LennardaJonesa:
φ
φ
  12   6 
  4 0      
 r  
 r 
0,2 – 0,5 nm – średnica atomu gazu
0 - min energii potencjalnej
r – odległość pomiędzy molekułami
σ - odl. pomiędzy molekułami przy której równoważą się siły przyciągania i
odpychania