TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w

TEORIA PASMOWA CIAŁ STAŁYCH
Skolektywizowane elektrony w metalu
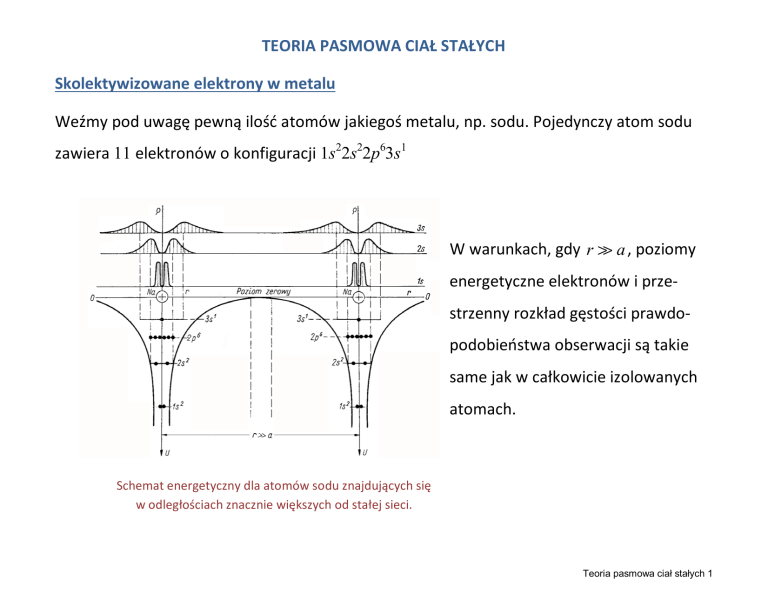
Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu
zawiera 11 elektronów o konfiguracji 1s22s22p63s1
W warunkach, gdy r  a , poziomy
energetyczne elektronów i przestrzenny rozkład gęstości prawdopodobieństwa obserwacji są takie
same jak w całkowicie izolowanych
atomach.
Schemat energetyczny dla atomów sodu znajdujących się
w odległościach znacznie większych od stałej sieci.
Teoria pasmowa ciał stałych 1
Skolektywizowane elektrony w metalu, cd.
W warunkach, gdy r ≈ a , w przypadku elektronów położonych blisko jądra, poziomy energetyczne elektronów i przestrzenny rozkład gęstości prawdopodobieństwa obserwacji są praktycznie takie same jak w izolowanych atomach.
Dla elektronów położonych na zewnętrznych powłokach poszczególne poziomy energetyczne przechodzą w pasma.
Ponadto, ze względu na obniżenie
barier potencjału pomiędzy sąsiednimi atomami, elektrony o najwyższych energiach uzyskują możliwość swobodnego poruszania się w
całej objętości kryształu.
Schemat energetyczny dla atomów sodu znajdujących się w odległościach rzędu stałej sieci.
Teoria pasmowa ciał stałych 2
Opis teoretyczny pasmowego charakteru widma energetycznego elektronów w metalu
W teorii ciała stałego, podobnie jak w teorii atomu, zasadniczym zadaniem jest określenie
widma energetycznego i stanów stacjonarnych skolektywizowanych elektronów w krysztale.
Ponieważ zagadnienie to jest bardzo złożone, dla uproszczenia rachunków stosuje się szereg
przybliżeń:
-
Przybliżenie adiabatyczne.
-
Przybliżenie jednoelektronowe.
-
Przybliżenie silnie związanych elektronów.
-
Przybliżenie elektronów swobodnych.
-
Przybliżenie słabo związanych elektronów.
Rozwiązania stacjonarnego równania Schrödingera, otrzymane z uwzględnieniem tych przybliżeń pokazują, że widmo energetyczne kryształu charakteryzują pasma energii dozwolonych o skończonej szerokości. Dla uzyskania informacji ilościowych w wielu przypadkach niezbędne są obliczenia numeryczne.
Teoria pasmowa ciał stałych 3
Przybliżenie adiabatyczne
Masa jąder jest znacznie większa od masy elektronów. Dlatego jądra poruszają się znacznie
wolniej. Kryształ może być traktowany jako składający się z dwóch niezależnych podukładów:
-
Prędkich elektronów,
-
Praktycznie nieruchomych jąder.
W ten sposób zagadnienie układu jąder i elektronów można sprowadzić do prostszego zagadnienia stanu samych elektronów w nieruchomej sieci jąder.
Przybliżenie jednoelektronowe
Pozwala zredukować problem ruchu wielu elektronów do zagadnienia ruchu jednego elektronu w wypadkowym polu jonów sieci i pozostałych elektronów, czyli do rozwiązania jednoelektronowego równania Schrödingera
2
−
∆ψ + Uψ =
Eψ
2m
U - energia potencjalna elektronu w polu jonów sieci i innych elektronów.
Teoria pasmowa ciał stałych 4
Przybliżenie silnie związanych elektronów
2
Celem rozwiązania równania −
Eψ korzystamy z postaci energii potencjalnej
∆ψ + Uψ =
2m
charakterystycznej dla obszaru silnego pola
=
U
(r ) U a (r ) + δ U (r )
Przypadek δ U (r ) = 0 (przybliżenie zerowe, kryształ bez oddziaływań)
Otrzymujemy ψ (r ) = ψ a (r ) , E = E (n, l ) - takie jak dla atomu izolowanego; każdy poziom
energetyczny jest N -krotnie zwyrodniały, gdzie N - liczba atomów w sieci.
Przypadek δ U (r ) ≠ 0 (kryształ)
Oddziaływanie to prowadzi do usunięcia zwyrodnienia i rozszczepienia danego poziomu niezwyrodniałego na N blisko siebie leżących podpoziomów, a w przypadku (2l + 1) krotnego
zwyrodnienia (bez uwzględnienia spinu) na N (2l + 1) podpoziomów.
Teoria pasmowa ciał stałych 5
Przybliżenie silnie związanych elektronów, przypadek δ U (r ) ≠ 0 , cd.
Ze względu na usunięcie zwyrodnienia elektronowych poziomów energetycznych, powstaje
pasmo dozwolonych energii.
Szerokość pasm energetycznych elektronów w krysztale w zależności od odległości między atomami. Przyjmując V ≈ 1 cm3 ,
otrzymujemy n ≈ 1022 atomów, co przy szerokości pasma np.
≈ 1 eV daje odległość między poziomami ≈ 10−22 eV . Widmo
energetyczne w paśmie jest więc praktycznie ciągłe.
Największe zmiany energii występują dla stanów elektronów w zewnętrznych powłokach, bo
na te elektrony pole sieci ma największy wpływ. Pasma energetyczne elektronów walencyjnych są najszersze. Zmiany energii elektronów wewnętrznych są nieznaczne.
Pasma energii dozwolonych są oddzielone pasmami energii wzbronionych. Ze wzrostem
energii szerokość pasm energii dozwolonych rośnie, a energii wzbronionych maleje.
Teoria pasmowa ciał stałych 6
Przybliżenie elektronów swobodnych
Przybliżenie to służy do opisu elektronów słabo związanych z atomami, np. elektronów
przewodnictwa w metalach. W przybliżeniu elektronów swobodnych kryształ przedstawia
się jako jamę energii potencjalnej o płaskim dnie
W przybliżeniu elektronów swobodnych nie bierze się pod
uwagę istnienia sieci krystalicznej, jej periodyczności ani
możliwości tworzenia tej sieci przez różne atomy.
Przez to model ten nie wyjaśnia istnienia pasm energetycznych, ani różnic pomiędzy ciałami stałymi
Model swobodnych elektronów pozwala dobrze opisać
m.in. ciepło właściwe, przewodność cieplną, przewodność
elektryczną. Model ten zawodzi, kiedy staramy się za jego pomocą wyjaśnić inne ważne zagadnienia, takie jak: np. różnice miedzy metalami i półmetalami, półprzewodnikami i izolatorami.
Teoria pasmowa ciał stałych 7
Przybliżenie słabo związanych elektronów (elektronów prawie swobodnych)
2
Celem rozwiązania równania −
Eψ korzystamy z postaci energii potencjalnej
∆ψ + Uψ =
2m
charakterystycznej dla obszaru słabego pola


U (r=
) U 0 + δ U (r )

r
U0 -

δ U (r )  U 0
- Wektor położenia.
Energia potencjalna elektronu w polu jonów dodatnich przy założeniu, że to
pole jest kompensowane przez pole wszystkich pozostałych elektronów

δ U (r )
prócz danego.
- Uwzględnia niecałkowitą kompensację pola przez elektrony. Funkcja okresowa o okresie równym stałej sieci.
W przybliżeniu słabo związanych elektronów model kryształu można przedstawić jako jamę
energii potencjalnej ze słabo pofalowanym dnem. Model ten wyjaśnia istnienie pasm energetycznych, a także przerw między nimi.
Teoria pasmowa ciał stałych 8
Metale w teorii pasmowej ciał stałych
Jedną z najważniejszych cech metali jest ich wysokie przewodnictwo elektryczne. Warunkiem, aby elektrony w krysztale mogły wytworzyć prąd elektryczny jest to, aby znajdowały
się w paśmie nie całkowicie zapełnionym. W paśmie
całkowicie zapełnionym każdemu elektronowi o

wektorze falowym k towarzyszy elektron o wekto
rze − k i odpowiednie przyczynki do prądu znoszą
się.
Rozszczepienie pasma 3s wynosi dla sodu ok.
5,5 eV . Jest ono tylko częściowo obsadzone, stąd
elektrony w tym paśmie mogą być łatwo przyspieszane przez zewnętrzne pole elektryczne i w ten
sposób brać udział w przewodnictwie prądu elektrycznego.
Rozszczepianie się atomowych poziomów energetycznych przy tworzeniu się kryształu przykładowego metalu
- sodu. Linią przerywaną pokazano rzeczywistą odległość sąsiednich atomów w krysztale.
Teoria pasmowa ciał stałych 9
Półprzewodniki w teorii pasmowej ciał stałych
Schematy pasm energetycznych
kryształów pierwiastków należących
do IV grupy układu okresowego.
Pod symbolami podano odległość
między sąsiednimi atomami.
W temperaturze 0 K półprzewodniki nie przewodzą prądu elektrycznego, gdyż pasmo walencyjne jest całkowicie obsadzone. W wyższych temperaturach (lub pod wpływem fotonów)
część elektronów przechodzi do pasma przewodnictwa i w ten sposób może brać udział w
przewodzeniu prądu.
Teoria pasmowa ciał stałych 10