(opracowanie modelu sieci neuronowej – tzw. perceptronu, jako

INŻYNIERIA BEZPIECZEŃSTWA
Leszek Pacholski
Systemy Ekspertowe
i
Sztuczna Inteligencja
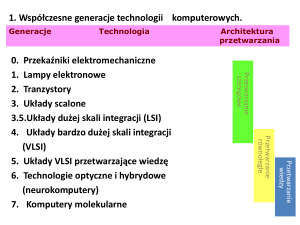
4. Rozwój badań nad Sztuczną Inteligencją na przestrzeni
ostatniego trzydziestolecia
Na bazie sztucznej inteligencji tworzone są tzw. systemy inteligentne,
których zadaniem jest komputerowe przetwarzanie wiedzy
w postaci symbolicznej i numerycznej.
Rozwój badań nad sztuczną inteligencją obejmuje dwa nurty:
- tworzenie fizycznych urządzeń lub ich symulacja komputerowa
(opracowanie modelu sieci neuronowej – tzw. perceptronu, jako
symulacji mózgu, który może być nauczony klasyfikowania
pewnego typu modeli na podobne lub różne),
-tworzenie i komputerowe aplikacje modeli sybolicznej
reprezentacji wiedzy oraz symbolicznego wnioskowania
(opracowanie symbolicznej reprezentacji problemu i
rozwiązywanie przy pomocy komputera prostych zagadek oraz
dowodzenie twierdzeń rachunku zdań).
8. Zastosowania Systemów Ekspertowych rozwiązywaniu
problemów NP-zupełnych.
Bariera złożoności
obliczeniowej dla problemów
NP-zupełnych
koszt
1. Dziedziny, z niepewną informacją
(wiedzą).
2. Dziedziny, które nie są w
jednoznaczny sposób sformalizowane
(nie istnieje model matematyczny
algorytmów rozwiązujących problem).
3. Rozwiązywanie problemów NPzupełnych (są opracowane teorie, lecz
niemożliwe jest ogarnięcie za pomocą
algorytmów wszystkich teoretycznie
możliwych przypadków, w rozsądnym
czasie).
Dla problemów NP-zupełnych
złożoność obliczeniowa (czyli liczba
kroków koniecznych do ich
rozwiązania) jest funkcją wykładniczą
ich rozmiarów (tzn. przy liniowym
wzroście wymiaru problemu czas
potrzebny na jego rozwiązanie
wzrasta wykładniczo)
Przetwarzanie
danych
Systemy
ekspertowe
złożoność obliczeniowa
11a. Metody symbolicznej reprezentacji wiedzy wykorzystujące
zasady logiki formalnej.
Rachunek zdań
Opis cech otaczającego świata formułujemy
w postaci zdań.
Wnioskowanie wywodzi się z logiki dwuwartościowej.
Zdania oznaczamy symbolami, np. A, B, C, D ... .
Mogą one być łączone za pomocą
spójników logicznych:
 negacja,  koniunkcja,  alternatywa,
 implikacja,  równoważność.
Łącząc zdania spójnikami można tworzyć wyrażenia
logiczne, tzw. formuły.
Formuły, które zawsze dają zdanie prawdziwe
niezależnie od wartości logicznych zmiennych
zdaniowych nazywamy tautologiami.
11b. Metody symbolicznej reprezentacji wiedzy wykorzystujące
zasady logiki formalnej.
Rachunek predykatów jest rozszerzeniem rachunku zdań
przez wprowadzenie: kwantyfikatora ogólnego x
oznaczającego, że formuła jest prawdziwa dla wszystkich
wartości związanych ze zmienną x,
oraz kwantyfikatora szczegółowego x oznaczającego,
że istnieje przynajmniej jedno znaczenie x, dla którego
związana formuła jest słuszna.
Rachunek predykatów składa się z: alfabetu, formalnego
języka, aksjomatów i reguł wnioskowania.
Alfabet zawiera: predykaty, zmienne, funkcje, stałe,
spójniki, kwantyfikatory i ograniczniki
(nawiasy, przecinki).
12a. Nieformalne metody symbolicznej reprezentacji wiedzy.
Stwierdzenia
Stwierdzenia są jednym z głównych elementów baz wiedzy.
Dotyczą: zdarzeń, zjawisk, objawów, czynności.
Najczęściej są zapisywane w postaci uporządkowanej trójki:
(<OBIEKT>, <ATRYBUT>, <WARTOŚĆ>)
Dla uproszczenia zapisów stwierdzeń stosuje się słowniki nazw obiektów i atrybutów
oraz ich wartości.
W niektórych systemach stwierdzenia są zapisywane w
postaci uporządkowanej czwórki:
(<OBIEKT>, <ATRYBUT>, <WARTOŚĆ>, <CF>)
gdzie CF jest stopniem pewności (Cerntainty Factor),
prowadząc do tzw. stwierdzeń przybliżonych.
Stopnie pewności wyznacza się subiektywnie (np. w
przedziale: [0,1] bądź [-1,1])
12b. Nieformalne metody symbolicznej reprezentacji wiedzy.
Wektory wiedzy
Wektory wiedzy są pewnego rodzaju uogólnieniem
regułowych metod reprezentacji wiedzy, dla których
stosujemy zapis reguł w postaci wektorowej.
Wykorzystujemy trzy symbole ilustracji wiedzy:
* – dany warunek/wniosek w regule nie występuje,
T – dany warunek/wniosek jest prawdziwy,
N – dany warunek/wniosek jest fałszywy.
12c. Nieformalne metody symbolicznej reprezentacji wiedzy.
Sieci semantyczne
Sieć semantyczna (Semantic Net)
jest pewnego rodzaju logiką,
w ramach której
relacje między obiektami są przedstawione
w postaci graficznej.
Jest tu więc, jak gdyby, wyrysowany
mechanizm dedukcji.
Wnioskowanie odpowiada
„poruszaniu się” po grafice.
Na podstawie inspekcji sieci wyprowadza
się różne konkluzje.
12d. Nieformalne metody symbolicznej reprezentacji wiedzy.
Systemy ramowe
Rama jest strukturą, opisującą dany obiekt
i składa się z podstruktur, tzw. klatek
(slots). Każda klatka reprezentuje pewną
właściwość albo cechę obiektu,
opisywanego przez ramę.
Ramy są podobne do reprezentacji wiedzy
za pomocą stwierdzeń:
(<obiekt> <atrybut> <wartość>).
W przypadku systemów ramowych mamy jednak
szerszy opis, ponieważ wartość zapisania w klatce
jest jednym z wielu możliwych elementów klatki.
Klatka dzieli się na mniejsze części –
fasety.
Każda: rama, klatka i faseta musi mieć
swoją nazwę.
16. Koncepcje wnioskowania rozmytego
Pojęcie zbioru rozmytego jest uogólnieniem pojęcia zbioru
ostrego, polegającym na dopuszczeniu, aby funkcja
charakterystyczna (tzw. funkcja przynależności) tego
zbioru - przyjmowała obok stanów krańcowych (jeden lub
zero {0,1}), również wartości pośrednie z tego przedziału
(odcinek [0,1]).
W przypadku zbioru rozmytego mamy więc płynne
przejście między całkowitą przynależnością i nie
przynależnością. Elementy mogą należeć do zbioru
również w pewnym stopniu.
W procesach wnioskowania naukowego często
wykorzystujemy koncepcję teorii zbiorów rozmytych
ponieważ pozwala ona na lepsze modelowanie granic
decyzyjnych dla rozmytych pojęć werbalnych.
18 a . Kształt zbioru rozmytego. Modyfikatory kształtu
zbioru rozmytego.
Modyfikatory zmieniające kształt zbioru rozmytego, spełniają podobną
rolę , jak przysłówki w języku naturalnym.
Mają za zadanie zmieniać znaczenie podstawowych terminów
wykorzystywanych do modelowania wiedzy.
Są heurezami, nie wynikającymi z teorii matematycznych.
Definiowane są wyłącznie na podstawie oceny „odpowiedniości”
wynikowych zbiorów rozmytych.
18 b . Kształt zbioru rozmytego. Modyfikatory kształtu
zbioru rozmytego.
18 c . Kształt zbioru rozmytego. Modyfikatory kształtu zbioru
rozmytego.
Zaletą trójkątnych zbiorów rozmytych jest bardzo prosta postać ich funkcji
przynależności (zbiór może być zdefiniowany przez trzy parametry: a, b, c).
Wartości funkcji mogą być znalezione przez prostą interpolację liniową:
18 d . Kształt zbioru rozmytego. Modyfikatory kształtu zbioru rozmytego.
Zaletą trapezoidalnych zbiorów rozmytych są właściwości zbliżone do
trójkątnych (zbiór może być zdefiniowany przez cztery parametry: a, b, c, d).
Wartości funkcji mogą być zapisane następująco :
18 e . Kształt zbioru rozmytego. Modyfikatory kształtu zbioru
rozmytego.
Do reprezentacji zbiorów nieograniczonych (takich jak np.: młody, dużo…)
wykorzystane mogą zostac zbiory rozmyte stanowiące fragmenty trapezów
złożone z krótszej podstawy oraz opadającego lub wznoszącego się
ramienia.
19 a . Aproksymacja lingwistyczna. Kwantowanie przestrzeni
wartości w rozmytych systemach ekspertowych.
Podstawą zdefiniowania zbioru wartości zmiennej
jest określenie tzw. terminów podstawowych
(pierwotnych).
Na ich podstawie tworzone mogą być zbiory rozmyte
opisujące terminy złożone, definiowane za pomocą
operatorów działań na zbiorach rozmytych oraz
modyfikatorów kształtu.
Proces kolejnego przekształcania terminów
pierwotnych, poprzez zastosowanie modyfikatorów,
tak aby wynikowy zbiór rozmyty w jak najlepszy
sposób opisywał modelowane pojęcie nazywamy
aproksymacją lingwistyczną.
19 b . Aproksymacja lingwistyczna. Kwantowanie przestrzeni
wartości w rozmytych systemach ekspertowych.
Typowym sposobem tworzenia terminów pierwotnych
dla poszczególnych zmiennych tworzonego systemu
jest równomierne kwantowanie przestrzeni wartości.
Polega ono na podzieleniu tej przestrzeni na określoną
liczbę zbiorów rozmytych o jednakowej szerokości.
Kwestia wyboru liczby i funkcji przynależności
terminów pierwotnych musi być przedmiotem
konsultacji budowniczego systemu z ekspertem.
W przypadku, gdy brak jest dostatecznej wiedzy dla
bezpośredniego określenia terminów pierwotnych,
możliwe jest otrzymanie funkcji przynależności na
podstawie analizy obserwacji zachowania
modelowanego systemu.
20. Proces defuzyfikacji we wnioskowaniu rozmytym.
Proces wnioskowania z wykorzystaniem reguł
rozmytych daje w wyniku rozmytą wartość zmiennej
wyjściowej. W wielu przypadkach niezbędna jest jej
zamiana na wartość dokładną. Wyznaczanie
dokładnej wartości zmiennej określonej za pomocą
zbioru rozmytego nazywamy wyostrzaniem lub
defuzyfikacją. Defuzyfikacja przeprowadzana jest
zwykle za pomocą jednej z dwóch metod: - środka
obszaru (metoda centroidu - COA), lub średniej
maksymalnej (MOM). Metoda COA polega na
znalezieniu środka ciężkości zbioru rozmytego;
metoda MOM natomiast polega na wyznaczeniu
środka obszaru o największej przynależności.
24 a. Modele proste i struktury perceptronowe
Sztucznych Sieci Neuronowych.
Najbardziej znanymi
prostymi modelami neuronu są:
d) model ADALINE
(Adaptive Linear Neuron),
a) model liniowy,
b) model nieliniowy skokowy
tzn. ogranicznik twardy,
e) model MADALINE
(Many Adaptive Linear Neurons).
c) model nieliniowy sigmoidalny,
24 b. Modele proste i struktury perceptronowe
Sztucznych Sieci Neuronowych
Poszczególne neurony są łączone w pewnego rodzaju
struktury, które tworzą sieci. Znanych około 50 typów
takich sieci, z czego 15 zyskało znaczenie praktyczne.
Sieć Hopfielda
Sieć Hamminga
Przykładowa
struktura perceptronu
wielowarstwowego
28a. Algorytmy Ewolucyjne – pojęcie, strategie działania,
podstawowe nurty rozwiązań.
Algorytm ewolucyjny jest adaptacyjną procedurą poszukiwania
rozwiązania dla zagadnień optymalizacyjnych, funkcjonującą
w zakodowanej przestrzeni rozwiązań i wykorzystującą
procesy losowe do określenia kierunku przeszukiwania.
Zbiór parametrów zadania optymalizacyjnego zakodowany jest
w postaci skończonego ciągu znaków, z pewnego skończonego
alfabetu i nazywany jest osobnikiem lub chromozomem.
Idea algorytmu ewolucyjnego polega na znalezieniu
takiego zestawu parametrów, który maksymalizuje
tzw. funkcję dopasowania.
Jest to funkcja wartościująca warianty rozwiązania
ze względu na lepsze lub gorsze rozwiązywanie problemu.
Oszacowanie funkcji dopasowania może dokonać się na drodze
heurystycznej; nie musi ona być zdefiniowana matematycznie.
Proces przeszukiwania realizowany jest iteracyjnie,
jednocześnie dla wielu ciągów znaków (zwanych populacją
osobników) reprezentujących pojedyncze rozwiązania.
28b. Algorytmy Ewolucyjne – pojęcie, strategie działania,
podstawowe nurty rozwiązań.
Trzy podstawowe nurty w zakresie algorytmów ewolucyjnych
dotyczą: algorytmów genetycznych, strategii ewolucyjnych,
programowania ewolucyjnego.
Strategia algorytmu ewolucyjnego polega na przemieszczaniu
się od jednej populacji rozwiązań do kolejnej w sąsiedztwie
całej populacji bezpośrednio ją poprzedzającej, zgodnie
z pewnymi ustalonymi regułami.
Do generowania sąsiedztwa populacji i przeszukiwania go
oraz do wybierania nowej generacji algorytm ewolucyjny
wykorzystuje operatory genetyczne: selekcji, krzyżowania
bądź mutacji.
Z punktu widzenia badań operacyjnych algorytmy ewolucyjne,
jako kategoria strategii lokalnego poszukiwania, współtworzą
klasę tak zwanych metaheurystycznych algorytmów
optymalizacyjnych.