Paweł Karol FRANKOWSKI
Wydział Elektryczny, Wydział Informatyki
Zachodniopomorski Uniwersytet Technologiczny w Szczecinie
E–mail: [email protected]
Wykorzystanie algorytmów Data Mining
do budowy modelu ekonomicznego
(na przykładzie GMC)
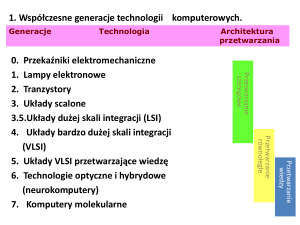
1. Wprowadzenie
Żyjemy w czasach społeczeństwa informacyjnego. W czasach obecnych tak jak nigdy
dotąd informacja staje się towarem. To czy potrafimy wyciągnąć poprawne wnioski
z posiadanych wiadomości może stanowić o rozwoju, lub upadku naszej firmy. Z drugiej strony olbrzymia ilość danych, do których mamy lub możemy mieć dostęp oraz
wszechobecny szum informacyjny sprawiają, że ważny jest nie tylko zakres i wiarygodność posiadanych informacji, ale również umiejętność sprawnego i efektywnego ich
przetworzenia. Postępująca globalizacja stawia przed nami nowe szanse i zagrożenia.
Sprzedaż przez Internet, oraz rozluźnienie przepisów celnych ułatwiają znacząco poszerzania oferty i wchodzenie na nowe rynki zbytu. Jednocześnie wskutek częstych zmian
pozycji graczy rynkowych posiadane informacje szybko się starzeją, a uzyskanie kompletnej i aktualnej wiedzy na temat rynku staje się coraz trudniejsze.
Konieczność uzdatniania, filtrowania i aproksymowania brakujących danych sprawiają,
że coraz większą popularnością cieszą się procedury, które pozwalają na przedstawienie
wiadomości w postaci umożliwiającej bezpośrednie wspomaganie decyzji. Tworząc
model ekonomiczny rynku musimy uwzględnić zarówno zjawiska i procesy zachodzące
wewnątrz firmy jak i te dotyczące naszego najbliższego otoczenia. Często konieczne
okazuje się również uwzględnienie danych makroekonomicznych dotyczących całego
segmentu, kraju, a nawet gospodarki światowej. Głównym zadaniem tworzonych narzędzi jest przewidywanie przyszłych skutków obecnych decyzji na podstawie danych
archiwalnych. Możliwość oszacowania krótko i długookresowych trendów rynkowych
oraz zachowań konkurencji pozwala lepiej przygotować strategię działania firmy, co
przekłada się na jej długofalowy sukces. Systemy informatyczne umożliwiają również
częściową automatyzację procesów decyzyjnych, znacznie usprawniając pracę analityków i menadżerów. Rola procedur prognozowania jest różna w różnych obszarach działalności firmy. Największe ich znaczenie można zaobserwować przede wszystkim
w zarządzaniu sprzedażą, produkcją, zasobami ludzkimi, zapasami i finansami.
W niniejszym opracowaniu autor korzysta między innymi z doświadczeń i danych
zgromadzonych podczas rozgrywek Global Management Challenge (w skrócie GMC).
GMC to największe międzynarodowe przedsięwzięcie oparte na symulacjach biznesowych, w którym uczestniczyło już ponad 400 000 osób na całym świecie (ponad
40
Paweł Karol Frankowski
40 krajów). Udział w zawodach biorą zarówno praktykujący menadżerowie firm jak
i studenci kierunków ekonomicznych i inżynierskich. O jakości modelów stosowanych
w symulacji może świadczyć rosnąca z edycji, na edycję liczba uczestników tak na
świecie jak i w kraju (w XIII polskiej edycji, której finał miał miejsce w tym roku
udział wzięło około 3 500 osób) [1].
2. Rynek jako układ nieliniowy
Każda firma stanowi swoisty mechanizm i tak jak w przypadku maszyny pojawiające
się problemy wynikają zwykle z zmian zachodzących albo wewnątrz mechanizmu, albo
w jego otoczeniu. Jeżeli przyjąć, że firma jest maszyną to jednym z głównych zadań
zarządu jest pełnienie funkcji regulatora. Regulator ten steruje firmą w taki sposób by
możliwie najłagodniej przechodziła przez wszelkiego typu zmiany i trudności. Decyzje
zarządu stanowią zatem swoisty sygnał sterujący u(t). Najpowszechniej stosowanym
w technice regulatorem jest regulator PID, w którym:
t
u (t ) = k p ⋅ ε (t ) + ki ⋅ ∫ ε (t ) + k d ⋅
0
dε (t )
dt
(1)
gdzie:
u(t) - sygnał sterujący;
ε(t) - uchyb, czyli różnica między wartością zadaną a wartością na wyjściu
w stanie nieustalonym;
kp - wzmocnienie części proporcjonalne;
ki - wzmocnienie części całkującej, równe
Ti - czas zdwojenia (całkowania);
ki = k p ⋅
1
Ti
;
kd - wzmocnienie części różniczkującej, równe kd=kp⋅Td;
Td - czas wyprzedzenia (różniczkowania).
Ideę regulatora PID można przełożyć na zarządzanie firmą. Człon proporcjonalny odpowiada podejmowanym decyzjom. Sygnał wejściowy w członie P, który w omawianym przypadku tworzą decyzje zarządu, jest proporcjonalny do sygnału wyjściowego,
czyli ich skutków. Niestety by podjęte decyzje mogły być trafne trzeba znać historię
firmy, trzeba wiedzieć jakie sygnały wejściowe w przeszłości generowały jakie efekty
na wyjściu. Pewna suma zainwestowana w promocje niewielkiego rodzinnego przedsięwzięcia da inny efekt niż ta sama kwota zainwestowana w wielkiej międzynarodowej
korporacji. Nie tylko rozmiar firmy ma tu znaczenie, inne bodźce mogą sprzyjać sprzedaży dóbr podstawowych, a inne dóbr luksusowych. Różnice będą zauważalne także
pomiędzy różnymi produktami i rynkami (np. inaczej na tę samą reklamę zareagują
odbiorcy na rynku krajowym, a inaczej na rynku azjatyckim). Człon całkujący odzwierciedla, zatem podatność obiektu (rynku) na dany bodziec. Podobnie jak w prawdziwym
regulatorze PID zapobiega on powstawaniu uchybu ustalonego, czyli powstawaniu
różnicy pomiędzy wartością zadaną, a otrzymaną. Ostatnim członem jest człon różniczkujący, jego zadaniem w regulatorach PID jest zapobieganie przeregulowaniu, które
Wykorzystanie algorytmów Data Mining do budowy modelu ekonomicznego…
41
w skrajnych przypadkach może prowadzić nawet do zniszczenia układu. W przypadku
firmy za przeregulowanie należy uznać działanie pod wpływem emocji. Z definicji
wynika, że powstaje ono zwykle w wyniku błędnego nastawienia regulatora (podjęcia
błędnych decyzji), lub niekorzystnych warunków zewnętrznych. Człon ten umożliwia
ograniczenie negatywnych skutków przeregulowania.
Zwykły regulator PID nie sprawdziłby się jednak w zarządzaniu prawdziwą firmą.
W teorii realizuje on swoje zadania, jednak model ten nie nadaje się do układów silnie
nieliniowych. Specyficznym dowodem nieliniowości układu o nazwie „człowiek” może
być ekonomiczne prawo malejącej użyteczności krańcowej. Mówi ono o tym, że każda
kolejna jednostka konsumowanego dobra dostarcza nam mniejszej korzyści niż poprzednia. Prawo to uwzględnia, że od pewnego momentu kolejne jednostki mogą dawać
korzyść ujemną. Prostym przykładem może być jedzenie ciastek. Pierwsze sprawia nam
zwykle przyjemność, tak więc korzyść jest duża. Zjedzenie trzeciego zwykle dostarcza
już mniej przyjemności. W pewnym momencie nie mamy już ochoty na następne, wtedy nasza korzyść jest równa zero. Kontynuowanie jedzenia zakończy się problemami
żołądkowymi, czyli nasza korzyść będzie ujemna. Prawo to nie opisuje jednak wszystkich przypadków. Zdarza się, że każda kolejna porcja oddziałuje mocniej niż poprzednia. Dzieje się tak w przypadku np. alkoholu. Rynki są tworzone przez ludzi, a zatem
i one są układami nieliniowymi. Bezpośrednim odpowiednikiem prawa malejących
korzyści jest w przypadku firm prawo malejących dochodów.
3. Model CRISP w analizie ekonomicznej
Przedstawiony na Rys.1 model CRISP został
zaproponowany w latach 90-tych. Obecnie jest
on uważany powszechnie za standardowy
w procesach modelowania danych w technologii Data Mining [2].
Tworzenie modelu wymaga by wszystkie cechy rozpatrywać osobno, uwzględniając jednocześnie powiązania pomiędzy nimi.
W pierwszym etapie zadaniem menadżera jest
zrozumienie problemu. Proces ten przebiega
dwukierunkowo. Rozumienie zagadnienia
pomaga zrozumieć dane, zaś rozumienie znaczenia danych prowadzi do zrozumienia pro- Rys. 1. Model CRISP
blemu. Proces ten ma, zatem charakter itera- Rys. 1. CRISP Model
cyjnym. Algorytmy DM pozwalają na znalezienie zależności, ale nie pomagają w sformułowaniu problemu badawczego. Jeśli użytkownik nie wie, czego szuka to prawdopodobnie tego nie znajdzie. W tej fazie bardzo
pomocne okazują się być podstawowe badania statystyczne. W modelach ekonomicznych analityk pracuje zwykle na danych liczbowych. Zbadanie poszczególnych zmiennych pozwala dokonać wstępnej selekcji danych i zorientować się w zagadnieniu.
42
Paweł Karol Frankowski
Załóżmy, że otrzymanym zadaniem jest analiza elastyczność popytu. Poprzez przebadanie statystyczne poszczególnych zmiennych i utworzenie macierzy korelacji można
zauważyć, co i w jaki sposób wpływa na zmianę badanego parametru. Już na tym etapie
sprawny analityk stwierdzi, że istnieje więcej niż jedna elastyczność. Zwykle należy
osobno przeanalizować:
•
•
•
elastyczność cenową (przewaznie mającą charakter nieliniowy),
elastyczność dochodową (elastyczność zależna od poziomu dochodów – zwykle bada
się ją poprzez analizę czynników makroekonomicznych),
elastyczność krzyżową (zmienia się wraz z ceną innego dobra).
Są to trzy podstawowe rodzaje, mogą jednak pojawić się również inne. Po podziale
należy przystąpić do dokładniejszego wyszukiwania predykatorów zmian wartości
każdej z elastyczności.
Etap drugi to przygotowanie danych i budowa modelu. Jakość modelu zależy od poprawności przygotowania danych, zaś przygotowanie danych od wyników, które otrzymano
w modelu. Ponieważ jakość jednego jest zależna, od jakości drugiego wskazany jest rozwój
iteracyjny. Dzięki analizie statystycznej oraz odpowiedniemu przetworzeniu danych istnieje
możliwość wyselekcjonowania interesujących nas zmiennych. Wybrane cechy poddajemy
filtracji i uzupełnieniu, a następnie dyskretyzacji. Podczas filtracji eliminujemy dane, które
w danym momencie nie są istotne, nie dostarczają żadnych informacji, lub o których można
powiedzieć, że nie są poprawne. Często poszczególne zmienne są niekompletne, gdy braki
nie są duże można próbować zaproksymować pewne wartości. W innym wypadku należy
wykluczyć taką zmienną z analizy. Kolejnym bardzo istotnym krokiem jest dyskretyzacja.
Do podstawowych rodzajów dyskretyzacji zaliczamy [3]:
•
•
•
•
•
podział równymi przedziałami - na N przedziałów równej długości,
podział przedziałami o równej częstości – na N przedziałów o zbliżonej ilości rekordów,
ChiMerge –zachowuje podobieństwo względnych częstości klas decyzyjnych
w przedziałach. Wykorzystuje on statystykę do podejmowania sekwencyjnie decyzji
o połączeniu wybranych dwóch przyległych przedziałów,
minimalizacja entropii warunkowej klas decyzyjnych,
modyfikacje algorytmów analizy skupień.
Dobór odpowiedniego algorytmu może mieć kluczowe znaczenie dla skuteczności modelu
ekonomicznego. Z wymienionych rodzajów żaden nie jest lepszy od pozostałych. Badania
przedstawione w [3] dowodzą, że skutki dyskretyzacji są zależne w głównej mierze od opracowywanych danych. Można jednak przyjąć, że elementarne metody, czyli podział na równe przedziały oraz równe częstości dają zwykle gorsze efekty niż trzy pozostałe.
Dyskretyzacje można również dzielić, na:
•
Metody lokalne niezależnie dyskretyzują wartości poszczególnych zmiennych
w określonych fragmentach dziedziny (wyznaczonych przez wartości innych zmiennych). Taki charakter ma np. dyskretyzacja stosowana w trakcie konstrukcji drzewa
decyzyjnego, która następuje zawsze dla pewnego węzła drzewa (i odpowiadającego
mu zbioru przykładów).
Wykorzystanie algorytmów Data Mining do budowy modelu ekonomicznego…
43
•
Metody globalne dyskretyzują jednolicie wartości atrybutów ciągłych dla całej dziedziny (niezależnie od wartości innych zmiennych).
• Metody bez nadzoru (unsupervised, class-blind) nie wykorzystują w procesie dyskretyzacji informacji o etykietach przykładów.
• Metody z nadzorem (supervised) biorą pod uwagę tę informację.
Bardzo istotna jest także decyzja, co do szerokości przedziałów, które nie mogą być zbyt
małe, ani zbyt duże gdyż w obu przypadkach prowadzić to może to pogorszenia wyników.
Ważnym zjawiskiem, które należy uwzględnić przy przygotowaniu danych jest liczba analizowanych zmiennych. Wraz ze wzrostem liczby predyktorów, wykładniczo rośnie nakład
obliczeń potrzebnych do poszukiwania optimum w przestrzeni parametrów budowanego
modelu. Zwykle lepiej jest posłużyć się uśrednionym parametrem powstałym z kilku różnych niż pozwolić na przerost liczby analizowanych danych. Przeprowadzone badania jednoznacznie wskazują, że w większości przypadków przy zbyt dużej ilości parametrów
otrzymywane wyniki były gorsze niż w przypadku analizy kilku najważniejszych (zjawisko
przeuczenia). O jakości parametru może świadczyć funkcja przyrostu informacji wykorzystująca miarę entropii stosowana w drzewach decyzyjnych, lub algorytmy wyszukujące
reguł asocjacji takie jak algorytmy Apriori, czy FP-Growth.
Po przygotowaniu danych można przystąpić do wyszukiwania reguł i opisywania ich
w modelu. W przypadku elastyczności cenowej do podstawowych reguł zalicza się:
•
•
•
•
zwiększanie ceny jest korzystne w przypadku popytu Epd < 1 (reguła nie uwzględnia
kosztów zmiany wielkości produkcji),
zmniejszanie ceny jest korzystne w przypadku popytu Epd > 1 (reguła nie uwzględnia
kosztów zmiany wielkości produkcji),
wpływ elastyczności dochodowej jest różny dla różnych dóbr:
+ dobra wyższego rzędu: Eyd > 1,
+ dobra normalne: Eyd = 1,
+ dobra pierwszej potrzeby, takie jak żywność: 1>Eyd>0,
+ dobra niższego rzędu: Eyd < 1,
wpływ elastyczności krzyżowej również jest różny dla różnych dóbr:
+ dobra substytucyjne: Exy > 0,
+ dobra niezależne: Exy = 0,
+ donra komplementarne: Exy < 0.
Gdy wartość elastyczności cenowej jest większa od jedności oznacza to, że popyt wzrasta szybciej niż czynnik wywołujący zmianę. Gdy elastyczność jest równa jeden zmiana
czynnika jest proporcjonalna do zmiany popytu zaś, gdy elastyczność cenowa wynosi
zero wówczas dany czynnik nie ma wpływu na popyt.
Kolejnym etapem jest testowanie, wiąże się on z ostatecznym doskonaleniem modelu
oraz sposobu dostosowywania danych. Po pomyślnym ukończeniu tego kroku model
jest gotowy do wdrożenia.
44
Paweł Karol Frankowski
4. Wykorzystanie logiki rozmytej w modelach
ekonomicznych
Jak już wspomniano głównym problemem pojawiającym się przy budowie modeli ekonomicznych są brak danych oraz nieliniowość układu. Utrudnienia te sprawiają, że
korzystne jest skorzystanie z zbiorów rozmytych. Logika rozmyta sprawdza się doskonale w układach silnie nieliniowych, oraz przy słabo opisanych danych. (Na jej bazie
powstała m.in. idea rozmytego regulatora PID.) Zwykle wykorzystuje się podejście
wielokryterialne. Polega ono na wyodrębnieniu istotnych atrybutów, pod kątem których
ocenia się badane zagadnienie.
Rys. 2. Wartość zmiennej „cena”
Fig. 3. Wartość zmiennej „jakość”
Rys. 2 Value of the variable – „price”
Fig. 3 Value of the variable – „quality”
Załóżmy, że celem jest sprawienie by model szacował, które z produktów spełniają
wymagania klientów. Wyodrębniamy, zatem kilka najważniejszych naszym zdaniem
cech, czyli np.: rodzaj, jakość, wielkość, cena. Parametrem wyjściowym będzie natomiast użyteczność dla klientów. Dużą zaletą tej metody jest posługiwanie się określeniami lingwistycznymi, zrozumiałymi dla przeciętnego człowiek np.: niska cena, mały
rozmiar itd. Umożliwia to proste i szybkie gromadzenie danych. Zaleta ta jest jednak
okupiona koniecznością tworzenia słownika wartości lingwistycznych. Jego zadaniem
jest określać, co konkretnie oznaczają przyjęte wartości. Na potrzeby modelowania
systemu ekspertowego przyjmowana jest zwykle jednolita postać wykorzystywanych
w nim zbiorów rozmytych. Typowe funkcje przynależności mają kształt trójkątny lub
dzwonokształtny (typu gaussowskiego). Wybrane zmienne są zarówno typu ciągłego
(np. cena), jak i symbolicznego (np. jakość).
Wykorzystanie algorytmów Data Mining do budowy modelu ekonomicznego…
45
Logika rozmyta pozwala na dużą elastyczność
działania systemu. Jakość, czy cena produktu niekoniecznie muszą lokować go dokładnie w jednej
z wyszczególnionych kategorii. Zastosowanie
wartości rozmytych pozwala na wyrażenie stanów
pośrednich każdej ze zmiennych. W sensie logiki
rozmytej ten sam produkt może być w pewnym
zakresie produktem klasy pierwszej, a w pewnym
drugiej (np. jakość wykonania lokuje go w najwyższej klasie, jednak czas gwarancji już nie). Ponieważ jakość nie przyjmuje wartości liczbowych,
wiec jako przestrzeń rozważanych obiektów dla
wartości rozmytych można przyjąć jakąś przestrzeń
abstrakcyjną np.: [0, 1]. Typowy sposób kwantowania przestrzeni wartości, polega na jej podzieleniu na określoną liczbę zbiorów rozmytych o jed- Rys. 4. Klasyfikacja danych
w fuzzy logic
nakowej szerokości. Nie jest to jednak regułą. Gdy
zbiory rozmyte modelu są ukończone można Rys. 4. Algorithm of fuzzy logic
przejść do budowy bazy wiedzy. Od klientów dodata classification
wiadujemy się, że: produkt drogi jest nieakceptowany, produkt o cenie umiarkowanej jest akceptowalny jeżeli będzie mały i będzie należał
do najwyższej klasy jakości itd. Najważniejszą zaletą logiki rozmytej jest fakt, że umożliwia ona budowę i działanie modelu, nawet, jeśli wiedza leżąca u jego podstaw jest mało
precyzyjna i dokładna. Ludzie w swoim rozumowaniu posługują się kategoriami
i związkami rozmytymi, zatem model stworzony w tej technologii jest mocno intuicyjny.
Proces interpretacji wyników w systemie rozmytym przedstawia rysunek 4. W omawianym przypadku celem jest poddanie analizie gotowych produktów by sprawdzić czy
spełniają wymagania klientów. Najpierw dane wejściowe przechodzą przez blok fuzyfikacji, gdzie przeprowadzana jest operacja rozmywania, czyli obliczania stopnia przynależności do poszczególnych zbiorów rozmytych. Tu badane produkty mogą zostać sklasyfikowany np. jako tani w stopniu 0,6 i zarazem w umiarkowanej cenie w stopniu 0,4,
o klasie III w stopniu 0,9 itd. Po rozmyciu dane są przesyłane do następnego bloku.
Aby przeprowadzenie obliczeń było możliwe blok inferencji musi zawierać: bazę reguł,
mechanizm inferencyjny i funkcje przynależności wyjścia modelu. Baza reguł zawiera
reguły logiczne uzyskane od klientów, określające zależności przyczynowo-skutkowe
istniejące w systemie pomiędzy zbiorami rozmytymi wejść i wyjść, np.:
JEŻELI (MAŁE) I (TANIE) TO (AKCEPTOWALNE)
JEŻELI (DROGIE) LUB ((KLEASY III) I (DUŻE)) TO (NIEAKCEPTOWALNE)
Inferencja składa się z następujących etapów:
1.
2.
3.
Podstawienie stopni spełnienia przesłanek do poszczególnych reguł.
Obliczenie stopnia aktywizacji konkluzji.
Określenie wynikowej postać funkcji przynależności wyjścia na podstawie
stopni aktywizacji konkluzji poszczególnych reguł.
46
Paweł Karol Frankowski
Wynikowa postać powstaje z wszystkich wykorzystanych reguł. Poddaje się ją defuzzyfikacji, czyli na podstawie danych wyjściowych z bloku inferencji klasyfikujemy obiekt
z wartości parametru wyjściowego. W opisywanym przypadku produkt akceptowalny,
lub produkt nieakceptowany.
5. Wnioski
Zaprezentowane w pracy metody pozwalają na szybką i sprawną analizę nawet niezbyt
dokładnych danych. Przedstawione reguły są zasadami ogólnymi, które można stosować do dowolnego typu danych, jednak ich największe atuty eksponują się głównie
w trudnych warunkach, zwłaszcza przy badaniu układów nieliniowych.
Literatura
1.
2.
3.
http://www.gmcpoland.pl/
Statistica, Krótki kurs Data Minieng, http://www.dataminer.pl
Stefanowski J.: Zaawansowana Eksploracja Danych, Poznań 2010
Streszczenie
Celem artykułu jest przedstawienie metod sztucznej inteligencji służących do budowy
modeli ekonomicznych. Wykorzystano do tego celu proste algorytmy logiki rozmytej
i modelu CRISP. W artykule zaproponowano by podczas budowy modelu postrzegać
rynek, jako obiekt nieliniowy. Do wstępnej obróbki danych wykorzystano proste metody statystyczne, następnie wyszukiwano reguły asocjacji stosując do tego celu algorytmy Apriori i FP-Growth. Wybrane metody przetestowano na danych pochodzących
z raportów symulacji biznesowej GMC.
Building an economic model using Data Mining
algorithms (of the example GMC)
Summary
The purpose of this paper is to present the artificial intelligence methods for building
economic model. CRISP model and simple fuzzy logic algorithms are proposed for this
purpose. This paper is presented market like a non-linear system. Preparing data for data
mining based on the simple statistic methods. Apriori and FP Growth algorihms are
proposed for search association rules. Selected methods were tested on the data from
GMC-simulation reports.