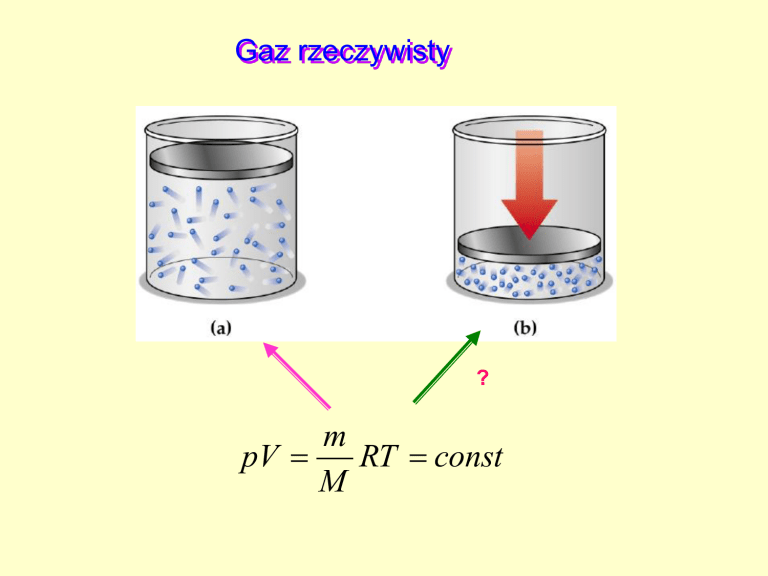
Gaz rzeczywisty
?
m
pV
RT const
M
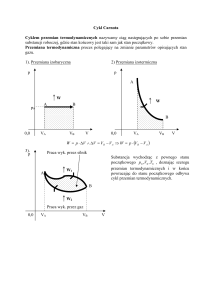
1 l azotu w warunkach normalnych, T = 273 K = const.
p [Atm]
pV [Atm·l]
1
100
200
500
1000
1.000
0.994
1.048
1.390
2.069
?
1 Atm = 1.01·105 Pa
pV const
gaz
ciecz
ciało stałe
Objętość gazu rzeczywistego nie może zmaleć poniżej
pewnej wartości granicznej b
b 4
objętość cząsteczek gazu
Pojawia się oddziaływanie miedzycząsteczkowe
(przyciąganie) – następuje wzrost ciśnienia wywieranego
na gaz
równanie van der Waalsa
dla 1 mola gazu rzeczywistego
a
p 2 V b RT
V
Johannes Diderik van der Waals 1837-1923
- oddziaływanie międzycząsteczkowe, stany
skupienia (szczególnie gazów), opracowanie
termodynamicznej teorii zjawisk
kapilarnych.
1910 - nagroda Nobla
a
p 2 V b RT
V
RT
a
p
2
V b V
p [Atm]
pV [Atm·l]
a
p 2 V b [Atm·l]
V
1
100
200
500
1000
1.000
0.994
1.048
1.390
2.069
1.000
1.000
1.009
1.014
0.893
Gazy rzeczywiste spełniają równanie van der Waalsa w
przybliżeniu. Gaz spełniający to równanie – gaz van der
Waalsa .
Doświadczalne izotermy CO2
T = 333K (60°C), 313 K (40°) - podobne
do izoterm gazu doskonałego.
Izoterma T = 304.1 K (31.1°C) - odbiega
kształtem od poprzednich (izoterma
krytyczna z punktem przegięcia K).
Izotermy dla T < 304.1 K zawierają
coraz dłuższe odcinki poziome,
odpowiadające układowi zawierającemu
ciecz i parę nasyconą.
Punkty B2, B1, K, C1, C2 wyznaczają tzw.
linię skroplenia.
Gałąź C2 , C1, K przedstawia linię cieczy,
a gałąź K, B1, B2 - linię pary nasyconej.
Obszar I - takie wartości ciśnienia,
objętości i temperatury, przy
których istnieje jedynie gaz. Obszar
II - para nasycona, obszar III ciecz w równowadze ze swą parą
nasyconą. W obszarze IV może
istnieć tylko ciecz.
Punkt K - punkt krytyczny - zaciera
się różnica między cieczą i gazem a
swobodna powierzchnia cieczy
przestaje istnieć.
W temperaturze T> Tk nie może
istnieć dana substancja w stanie
ciekłym. Przejście w stan ciekły
następuje po oziębieniu gazu poniżej
temperatury krytycznej.
Wzór barometryczny
p dp
p
h dh
h
Ciśnienie na wysokości
dh 0, dp 0
h dh
wynosi
p dp
. Dla
p p dp gdh
dp gdh
Powietrze w warunkach bliskich warunkom normalnym
zachowuje się jak gaz doskonały. Gęstość powietrza
m
pV
RT
M
Mg
dp
pdh
RT
m pM
V
RT
Przyjmujemy T = const
dp
Mg
p RT dh
Mg
ln p ln C
h
RT
Dla
h 0 p p0
Mg
ln p
h const
RT
ln C
Mg
p C exp
h
RT
Mg
p0 C exp
h
RT
1
Mg
p p0 exp
h
RT
ciśnienie
5
1,0x10
p0 = 105 Pa
T = 300 K
M = 29 kg/kmol
g = 10 m/s2
4
8,0x10
4
6,0x10
4
4,0x10
4
2,0x10
0,0
0
20
40
60
80
wysokość
100
Jak temperatura i ciśnienie powietrza zależą od wysokości?
Przyjmijmy, że nie ma wymiany ciepła pomiędzy warstwami
atmosfery – przemiana adiabatyczna.
1
T p
const
ln T 1 ln p ln c
dT
dp
1 0
T
p
dp
dT
dT
1 T 1 T
p
równanie różniczkowe adiabaty
dp
Mg
dh
p
RT
dT
Mg
dh
1 T
RT
Gradient temperatury
dT
Mg 1
dh
R
dT
Mg 1
0
dh
R
Ze wzrostem wysokości
temperatura powietrza
maleje
kg
m
0.029
9.81 2 1.41 1
dT
mol
s
J
dh
1.41 8.31
mol K
K
3 K
9.95 10
9.95
m
km
Rzeczywisty gradient temperatury – 6.5 K/km – para
wodna ulega kondensacji – wydzielające się przy tym ciepło
zmniejsza szybkość chłodzenia powietrza.
Po uwzględnieniu gradientu temperatury
Mg 1
p p0 1
h
RT0
1
R
Mg
p T0
h 1
p0
Znając wielkość pionowego gradientu temperatury i
mierząc wartość ciśnienia można wyznaczyć wysokość h.
1,1
1,0
0,9
0,8
0,7
p
p0
0,6
0,5
0,4
T
0,3
T0
0,2
0,1
0,0
0
1000
2000
3000
4000
5000
6000
7000
h [m]
8000
Wzór barometryczny
R
p Mg T0
h 1
p0
stosuje się do wysokości h 11 km . Dla 11 km h 25 km
ph11
h 11000 6340 ln
p
Dlaczego tak jest?
powietrze zjonizowane –
maleje przezroczystość
optyczna, pochłanianie
promieniowania – wzrost
temperatury do ponad
1000ºC na wysokości 500
km
stężenie ozonu maleje oziębianie
zwiększona zawartość
ozonu pochłaniającego
promieniowanie słoneczne
obszar izotermiczny
prądy powietrzne
wstępujące i zstępujące
Druga zasada termodynamiki
Sformułowana na podstawie obserwacji pracy maszyn cieplnych. Przy
przemianach ciepło
praca mechaniczna obowiązuje I zasada
termodynamiki. Ale jest niewystarczająca. Przemiana ciepłą w pracę
podlega pewnym ograniczeniom
praca
ciepło
ciepło –
praca –
T = const?
T = const?
Druga zasada termodynamiki stwierdza, że nie możemy zamienić ciepła
na pracę w stałej temperaturze.
Ciepło nie może być pobrane i zamienione na pracę w stałej
temperaturze bez dodatkowych zmian w układzie lub
otoczeniu
Sadi Carnot
Silnik cieplny
zbiornik ciepła
Silnik
• pobiera ze zbiornika ciepło
• wykonuje pracę
• przekazuje ciepło do chłodnicy
Z I zasady termodynamiki
chłodnica
QC QH W
Inne sformułowania II zasady termodynamiki
Silnik cieplny, działający periodycznie i nie zasilany żadną inna formą
energii, musi pobierać ciepło ze źródła o temperaturze wyższej od
najzimniejszego ciała w otoczeniu.
Nie istnieją periodycznie działające silniki takie, dla których jedynym
wynikiem działania byłoby uzyskiwanie pracy mechanicznej kosztem
ciepła pobranego z jednego tylko zbiornika.
Perpetuum mobile drugiego rodzaju (urządzenie, które stale
dostarczałoby pracę kosztem pobranego z otoczenia ciepła
zamienianego całkowicie na pracę) jest niemożliwością
II zasada wiąże się z faktem, że w przyrodzie występują zjawiska
nieodwracalne, biegnące samorzutnie tylko w jednym kierunku
Proces nieodwracalny
F
Praca wykonana na pokonanie sił tarcia
zamienia się na ciepło
Q
Czy doprowadzona energia cieplna
zamieni się na energię kinetyczną kostki?
Silniki odwracalne
Idealny silnik – pracujący bez strat – odpowiednik ruchu bez tarcia.
Analogia mechaniczna – kierunek przebiegu zjawisk mechanicznych
przebiegających bez tarcia można łatwo odwrócić – wystarczy
zadziałać niewielką siłą w danym kierunku.
Idealny silnik - niewielka zmiana temperatury zmienia kierunek
przepływu ciepła
T T
T
Nieznacznie
ogrzewamy ciało
z lewej strony
T T
T
Ciepło płynie zawsze pomiędzy
dwoma ciałami o tej samej
temperaturze – nieskończenie
mała różnica temperatur określa
kierunek jego przepływu –
przepływ odwracalny.
Nieznacznie
oziębiamy ciało
z lewej strony
Idealny silnik – silnik odwracalny – każdy proces można odwrócić –
dokonując małych zmian zmienić bieg silnika na przeciwny.
Gaz doskonały zamknięty tłokiem poruszającym się bez tarcia w
cylindrze
Gaz w kontakcie ze zbiornikiem ciepła – ogrzewamy gaz i rozprężamy
równocześnie – przy powolnych zmianach objętości temperatura = T2 izotermiczne rozszerzanie
Szybko wyciągamy tłok – temperatura szybko spada poniżej T2 i
przemiana nie jest odwracalna.
Gaz rozprężamy adiabatycznie, ΔQ = 0, temperatura maleje do
wartości T1 – ciepło nie dopływa ze zbiornika.
Gaz sprężamy izotermicznie w kontakcie z chłodnicą – ciepło odpływa z
cylindra.
Gaz sprężamy adiabatycznie – aż temperatura wrośnie do wartości T2.
Cykl możemy powtarzać, również w odwrotnej kolejności.
Praca wykonana podczas cyklu
W pdV
jest równa powierzchni ograniczonej krzywą
Żaden silnik pracujący
pomiędzy takimi samymi
temperaturami jak silnik
Carnot nie może wykonać
większej pracy.
Silnik (cykl) Carnot
Sprawność silnika idealnego
Sprawność silnika
wykonana praca
pobrane ciepło
W
Q2
Q W dU
1. Izotermiczne rozszerzanie, U = const, praca wykonana przez
gaz
2
W12 pdV
1
jest równa pobranemu ciepłu Q2
V2
2
W12
NkT2
V2
Q2 pdV
dV NkT2 ln
V
V1
1
V
1
Wykorzystaliśmy równanie
pV NkT
Podczas sprężania izotermicznego
V4
NkT1
W34 Q1
dV
V
V3
, N – liczba atomów
V4
NkT1 ln
V3
W W12 W34 Q2 Q1
Równanie adiabaty
TV 1 const
T2V2
1
1
V2
1
V1
1
T1V3
1
V3
1
V4
V2
Q2 NkT2 ln
V1
V3
Q1 NkT1 ln
V4
1
T2V1
1
T1V4
V2 V3
V1 V4
Q2 T2
Q1 T1
Q2 T2
Q1 T1
W Q2 Q1
Ta własność jest słuszna dla
każdego silnika odwracalnego
– nie tylko silnika z gazem
doskonałym
W Q2 Q1
Q1
T1
1
1
Q2
Q2
Q2
T2
T1
1
T2
Sprawność wszystkich odwracalnych silników, pracujących w
identycznych warunkach – (T1, T2) – jest jednakowa i określona
wartościami temperatury zbiornika ciepła i chłodnicy
twierdzenie Carnota