darek - Gazeta.pl

Środa 5 listopada 2014 Gazeta Wyborcza wyborcza.pl
Jeśli podstawą graniastosłupa byłby kwadrat o boku 4 cm, to
Jacek również zużyłby wszystkie klocki i graniastosłup miałby
32 cm wysokości.
Jeśli podstawą graniastosłupa byłby kwadrat o boku 6 cm, to
Jacek zużyłby 3 u 3 u 7 63 klocki i graniastosłup miałby 14 cm
wysokości.
Zatem druga zbudowana bryła to prostopadłościan o wymiarach 6 u 6 u14 . Pole powierzchni całkowitej tego prostopadłościanu jest równe 2 ˜ 6 ˜ 6 4 ˜ 6 ˜ 14 408 cm 2
384 16
Szukany stosunek jest równy
.
408 17
POZIOM ROZSZERZONY
Zadanie 1. (1 punkt)
Wielomian W x x 4 2 x 3 cx 4 jest podzielny przez
dwumian x – 2. Wynika stąd, że
A. c=4
B. c=–4
C. c=–2
D. c=2
Rozwiązanie: Jest to przykład zadania zamkniętego, za pomocą którego bada się znajomość tych haseł programowych, które
odróżniają poziom podstawowy od rozszerzonego. Do rozwiązania tego zadania wygodnie jest zastosować Twierdzenie Bézouta:
Wielomian W(x) jest podzielny przez dwumian x–p wtedy
i tylko wtedy, gdy W(p)=0.
4
Stąd W 2 2 2 ˜ 23 c ˜ 2 4 2c 4 zatem 2c 4 0
czyli c 2 . Należy więc w karcie odpowiedzi zaznaczyć odpowiedź D.
Zadanie 2. (2 punkty)
4
2 x 15
dla
6 x2
wszystkich liczb rzeczywistych x takich, że x z 6 i x z 6.
Oblicz wartość pochodnej tej funkcji w punkcie x=1. Zakoduj cyfrę jedności, cyfrę części dziesiętnych i cyfrę części setnych rozwinięcia dziesiętnego otrzymanego wyniku.
To przykład zadania nowego typu – z kodowaną odpowiedzią.
Zadania kodowane będą oceniane w sposób „skwantowany”, to
znaczy, że zdający otrzymuje albo dwa punkty albo zero. Nie ma
możliwości otrzymania jednego punktu. Aby uzyskać punkty za
rozwiązanie, zdający musi przedstawić do oceny efekt swoich
obliczeń w dokładnie takiej postaci, jaka jest zapisana w poleceniu. Nie jest zatem oceniany sposób znalezienia rozwiązania, lecz
tylko ostateczny wynik. Przygotowanie się do egzaminu będzie
wymagało zwrócenia uwagi na sprawność rachunkową. Zadania
z kodowaną odpowiedzią będą najczęściej związane z zastosowaniem typowego algorytmu. Zamieszczenie w arkuszu egzaminacyjnym zadań tego typu umożliwi otrzymanie punktów przez
tych zdających, którzy dobrze opanowali materiał teoretyczny
i nie popełniają błędów w obliczeniach, a być może mają kłopoty z rozwiązywaniem zadań wymagających mniej typowego rozumowania.
Dana jest funkcja f określona wzorem f x Rozwiązanie: Obliczamy pochodną funkcji f:
f c x 2 x4 15c 6 x 2 2x 4 156 x 2c
2 2
8 x3
6 x 6 x 2x 2x 15
6 x 2
4
2 2
2x 2x 4 24x 2 15
2 2
6 x Stąd
2 2 24 15 74
2,96
5
25
Należy więc zakodować, kolejno, cyfry: 2, 9, 6.
Sposób kodowania nie został jeszcze ostatecznie ustalony.
Rozważane są dwie wersje. Pierwsza, gdy odpowiedź zdającego
ocenia egzaminator, wówczas zdający zapisuje w arkuszu, w wyznaczonym miejscu wynik swoich obliczeń:
f c 1
2
Gdyby ocenę wykonywał system informatyczny, zdający zakoduje wynik na karcie odpowiedzi w odpowiedniej matrycy:
edulandia.pl 25
kuetapowych algorytmów lub przeprowadzaniem dowodów zarówno algebraicznych, jak i geometrycznych. W zadaniach tego
typu wyróżnia się, zgodnie z holistycznym sposobem oceniania,
kategorie rozwiązań i kwalifikuje przedstawione rozwiązanie do
odpowiedniej klasy, co łączy się z przyznaniem odpowiedniej dla
danej kategorii liczby punktów.
W przypadku zadania trzypunktowego, wyróżnione są cztery kategorie:
– rozwiązanie, w którym jest brak postępu – 0 p.
– rozwiązanie, w którym jest istotny postęp – 1 p.
– pokonanie zasadniczych trudności zadania – 2 p.
– rozwiązanie pełne – 3 p.
Oczywiście w przypadku konkretnego zadania, kategorie te
są dokładnie opisane w kontekście tego zadania.
Bardzo często „tworzywem” budowania zadań otwartych
rozszerzonej odpowiedzi są: kombinatoryka, stereometria, geometria analityczna i zastosowanie rachunku pochodnych do
rozwiązywania problemów optymalizacyjnych. Prawie zawsze
zadania tego typu wymagają zbudowania odpowiedniego modelu, starannego zaplanowania swoich czynności, często w dość
złożonych sytuacjach. W przygotowaniach do egzaminu maturalnego warto zwrócić szczególną uwagę na zadania związane
z problemami optymalizacyjnymi, które są wyraźnie uwypuklone w nowej podstawie programowej. Po raz pierwszy od wielu lat w trakcie egzaminu maturalnego zdający będą musieli posłużyć się rachunkiem różniczkowym, i to w kontekście praktycznym.
Poniżej przykład zadania otwartego rozszerzonej odpowiedzi dotyczącego problemów optymalizacyjnych.
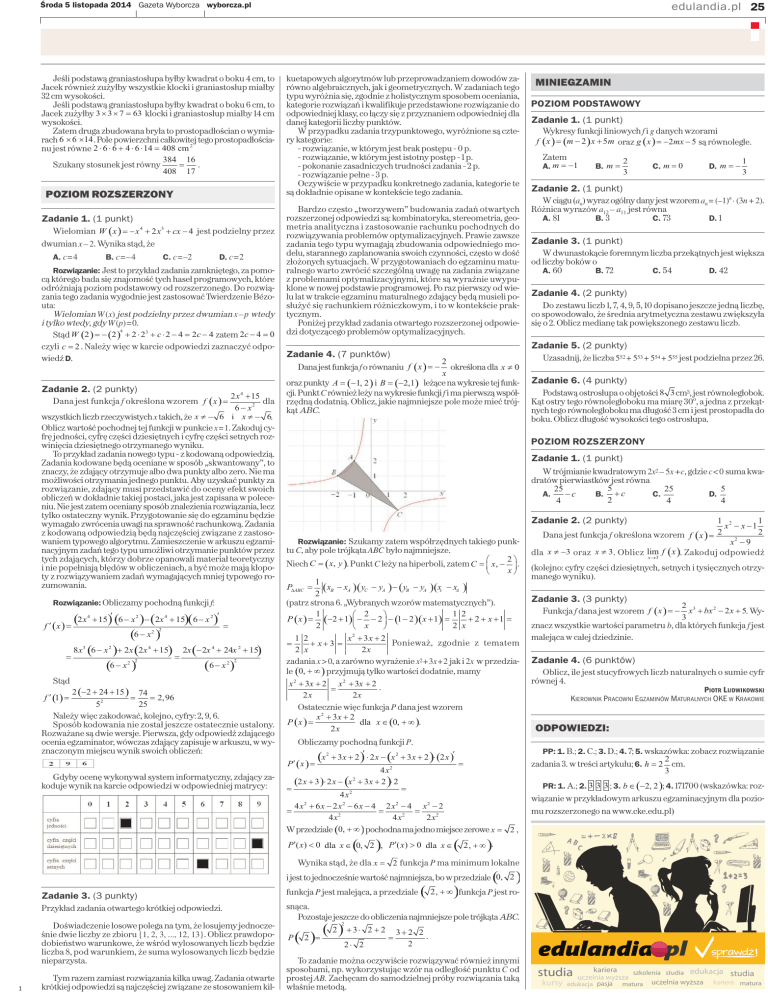
2
określona dla x z 0
x
oraz punkty A 1, 2 i B 2,1 leżące na wykresie tej funkcji. Punkt C również leży na wykresie funkcji f i ma pierwszą współrzędną dodatnią. Oblicz, jakie najmniejsze pole może mieć trójkąt ABC.
Dana jest funkcja f o równaniu f x 1
2
3
B. m
C. m
0
D. m
1
3
Zadanie 2. (1 punkt)
W ciągu (an) wyraz ogólny dany jest wzorem an = (–1)n . (3n + 2).
Różnica wyrazów a12 – a11 jest równa
A. 81
B. 3
C. 73
D. 1
Zadanie 3. (1 punkt)
W dwunastokącie foremnym liczba przekątnych jest większa
od liczby boków o
A. 60
B. 72
C. 54
D. 42
Zadanie 4. (2 punkty)
Do zestawu liczb 1, 7, 4, 9, 5, 10 dopisano jeszcze jedną liczbę,
co spowodowało, że średnia arytmetyczna zestawu zwiększyła
się o 2. Oblicz medianę tak powiększonego zestawu liczb.
Uzasadnij, że liczba 552 + 553 + 554 + 555 jest podzielna przez 26.
Zadanie 6. (4 punkty)
Podstawą ostrosłupa o objętości 8 3 cm3, jest równoległobok.
Kąt ostry tego równoległoboku ma miarę 30o, a jedna z przekątnych tego równoległoboku ma długość 3 cm i jest prostopadła do
boku. Oblicz długość wysokości tego ostrosłupa.
Zadanie 2. (2 punkty)
Rozwiązanie: Szukamy zatem współrzędnych takiego punktu C, aby pole trójkąta ABC było najmniejsze.
2·
§
Niech C x, y . Punkt C leży na hiperboli, zatem C ¨ x, ¸ .
x¹
©
1
P'ABC
xB xA yC yA yB yA xc xA 2
(patrz strona 6. „Wybranych wzorów matematycznych”).
1
2
1 2
P x 2 x 1
2 1§¨ 2 ·¸ 1 2 x 1
2
2 x
© x
¹
1 2
x2 3 x 2
Ponieważ, zgodnie z tematem
x3
2 x
2x
zadania x > 0, a zarówno wyrażenie x2 +3x+2 jak i 2x w przedziale 0, f przyjmują tylko wartości dodatnie, mamy
x 2 3x 2 x 2 3x 2
.
2x
2x
Ostatecznie więc funkcja P dana jest wzorem
x 2 3x 2
P x dla x  0, f .
2x
Obliczamy pochodną funkcji P.
x 2 3x 2 c ˜ 2 x x 2 3x 2 ˜ 2 x c
Pc x 4 x2
2
2 x 3 ˜ 2 x x 3x 2 ˜ 2
1 2
1
x x 1
2
2
Dana jest funkcja f określona wzorem f x x2 9
dla x z 3 oraz x z 3 . Oblicz lim f x . Zakoduj odpowiedź
x o3
(kolejno: cyfry części dziesiętnych, setnych i tysięcznych otrzymanego wyniku).
Zadanie 3. (3 punkty)
2
Funkcja f dana jest wzorem f x x 3 bx 2 2 x 5. Wy3
znacz wszystkie wartości parametru b, dla których funkcja f jest
malejąca w całej dziedzinie.
Zadanie 4. (6 punktów)
Oblicz, ile jest stucyfrowych liczb naturalnych o sumie cyfr
równej 4.
PIOTR LUDWIKOWSKI
KIEROWNIK PRACOWNI EGZAMINÓW MATURALNYCH OKE W KRAKOWIE
ODPOWIEDZI:
PP: 1. B.; 2. C.; 3. D.; 4. 7; 5. wskazówka: zobacz rozwiązanie
2
zadania 3. w treści artykułu; 6. h 2 cm.
3
PR: 1. A.; 2. 3 3 3 ; 3. b  2, 2 ; 4. 171700 (wskazówka: roz-
wiązanie w przykładowym arkuszu egzaminacyjnym dla poziomu rozszerzonego na www.cke.edu.pl)
2,
2, f .
2 funkcja P ma minimum lokalne
i jest to jednocześnie wartość najmniejsza, bo w przedziale 0, 2
1
Zatem
A. m
W trójmianie kwadratowym 2x2 – 5x+c, gdzie c< 0 suma kwadratów pierwiastków jest równa
5
25
25
5
c
A.
B. c
C.
D.
2
4
4
4
Wynika stąd, że dla x
Tym razem zamiast rozwiązania kilka uwag. Zadania otwarte
krótkiej odpowiedzi są najczęściej związane ze stosowaniem kil-
Wykresy funkcji liniowych f i g danych wzorami
f x m 2 x 5m oraz g x 2mx 5 są równoległe.
Zadanie 1. (1 punkt)
Doświadczenie losowe polega na tym, że losujemy jednocześnie dwie liczby ze zbioru {1, 2, 3, ..., 12, 13}. Oblicz prawdopodobieństwo warunkowe, że wśród wylosowanych liczb będzie
liczba 8, pod warunkiem, że suma wylosowanych liczb będzie
nieparzysta.
Zadanie 1. (1 punkt)
POZIOM ROZSZERZONY
Pc( x) 0 dla x  0, 2 , Pc( x) ! 0 dla x 
Przykład zadania otwartego krótkiej odpowiedzi.
POZIOM PODSTAWOWY
Zadanie 5. (2 punkty)
Zadanie 4. (7 punktów)
4 x2
4 x2 6 x 2 x2 6 x 4 2 x2 4 x2 2
4x2
4x2
2x2
W przedziale 0, f pochodna ma jedno miejsce zerowe x
Zadanie 3. (3 punkty)
MINIEGZAMIN
funkcja P jest malejąca, a przedziale
2, f funkcja P jest ro-
snąca.
Pozostaje jeszcze do obliczenia najmniejsze pole trójkąta ABC.
2
2 3˜ 2 2 3 2 2
.
P 2
2
2˜ 2
To zadanie można oczywiście rozwiązywać również innymi
sposobami, np. wykorzystując wzór na odległość punktu C od
prostej AB. Zachęcam do samodzielnej próby rozwiązania taką
właśnie metodą.
studia
kursy
kariera
uczelnia wyższa
edukacja pasja
szkolenia studia
matura
edukacja studia
uczelnia wyższa
kariera matura