teoria produkcji

Podstawy teorii producenta - teoria produkcji
Teoria produkcji jest analizą relacji, jakie występują między nakładem czynników
produkcji a osiąganym z tego nakładu produktem.
I. Funkcja produkcji
Obrazuje zależność między wielkością poniesionych nakładów
(ilością czynników
produkcji) na produkcję dóbr a osiągniętymi wynikami (ilość wytworzonego produktu).
Przy założeniu dwóch czynników produkcji: pracy –L i kapitału – K, funkcja produkcji jest
równa:
X=f(L,K),c.p.
W kontekście funkcji produkcji mówi się o tzw. efektywności technicznej produkcji,
czyli sytuacji, w której producent maksymalizując efekt produkcji nie będzie wkładał do
produkcji więcej czynników aniżeli jest to konieczne dla osiągnięcia tego poziomu efektu.
Funkcja produkcji wskazuje technicznie (a nie ekonomicznie) możliwą wielkość produkcji.
Po włączeniu kosztów czynników produkcji do analizy możliwości producenta uzyskamy
rzeczywistą wielkość produkcji, jaką może on wytworzyć przy danym poziomie kosztów.
Wówczas będziemy mówili o efektywności ekonomicznej produkcji, czyli sytuacji
polegającej na takim wykorzystaniu nakładów czynników produkcji, aby koszt
wytworzenia jednostki produktu był minimalny. Efektywność ekonomiczna oznacza wybór
w oparciu o zasadę najmniejszego kosztu produkcji.
Dokonując wyboru metod wytwarzania, producent powinien kierować się kryterium
efektywności ekonomicznej i technicznej. Oba jednak optima producenta będą optimami
cząstkowymi. Dopiero po uwzględnieniu relacji pomiędzy kosztami i przychodami
określimy warunki pełnej równowagi producenta.
FUNKCJA HOMOGENICZNA – funkcja, w której nakład czynników oraz efekty rosną o ten
sam procent.
FUNKCJA PRODUKCJI COBBA – DOUGLASA (funkcja C – D)
Funkcja ta ma postać:
X  AL K  ,
gdzie: X – wielkość produkcji, L – nakłady pracy, K – nakłady kapitału, A – wielkość
produkcji możliwa do uzyskania przy jednostkowym nakładzie czynników K i L, α i β –
zależność między przyrostem nakładów a przyrostem produkcji.
Zakładając niezmienioną metodę produkcji, taki sam przyrost nakładu pracy i kapitału
(czyli
dK dL

) oraz różniczkując funkcję produkcji C-D, otrzymujemy równanie:
K
L
dX dL
dK

(   ) 
(   ),
X
L
K
które oznacza, że:
- więcej niż proporcjonalny przyrost produkcji wynikający z proporcjonalnego
zwiększenia obu nakładów czynników produkcji (L i K), gdy α + β > 1. Mówimy
wówczas o rosnących korzyściach skali,
- proporcjonalny wzrost produkcji wynikający z proporcjonalnego zwiększenia obu
nakładów czynników produkcji (L i K), gdy α + β = 1. Mówimy wówczas o stałych
korzyściach skali,
-
mniej niż proporcjonalny przyrost produkcji wynikający z proporcjonalnego
zwiększenia obu nakładów czynników produkcji (L i K), gdy α + β < 1. Mówimy
wówczas o malejących korzyściach skali.
FUNKCJA PRODUKCJI W KRÓTKIM OKRESIE CZASU
Krótki okres czasu zakłada brak zmian w obszarze technologicznym, czyli technologia
produkcji jest dana.
Przyjmując następujące założenia do analizy funkcji produkcji, iż:
- istnieje tylko jeden czynnik zmienny - praca,
- istnieje jeden czynnik stały – kapitał,
- technologia produkcji jest dana,
- czynniki produkcji mogą łączyć się ze sobą w różnych proporcjach,
- produkt jest jednorodny,
otrzymujemy jednoczynnikową funkcję produkcji:
X=f(L), c.p.
Oznacza ona, iż wielkość produkcji jest tym większa (c.p.) , im więcej pracowników
zatrudnia przedsiębiorstwo. W związku z tym mamy do czynienia z następującymi
kategoriami ekonomicznymi:
1. produkt marginalny – jest to przyrost wielkości produkcji spowodowany przyrostem
zatrudnienia o 1, czyli:
MPPL 
dTPP
,
dL
gdzie: dTPP – miana wielkości produkcji spowodowana zmianą zatrudnienia o 1,
2. produkt przeciętny
zatrudnionego, czyli:
–
jest
to
ilość
APPL 
produkcji
przypadająca
na
jednego
TPP
.
L
3. produkt całkowity – całkowita ilość produkcji wytworzonej, przy stałym poziomie
kapitału i zmiennym czynniku pracy, czyli:
TPP  APPL  L.
ZALEŻNOŚĆ: PRODUKT CAŁKOWITY, MARGINALNY I PRZECIĘTNY
1. W punkcie przegięcia krzywej produktu całkowitego zaczyna działać prawo
malejącego produktu marginalnego (prawo malejącej produkcyjności
krańcowej), które oznacza, iż wraz ze zwiększaniem zatrudnienia czynnika
zmiennego produkcji (c.p.) następuje moment, kiedy każdy dodatkowy wzrost
zatrudnienia tego czynnika powoduje coraz mniejsze przyrosty produktu całkowitego.
Produkt marginalny początkowo wzrasta po czym zaczyna spadać. Zwiększanie
zatrudnienia poza punkt, gdy produkt marginalny równy jest zeru, prowadzi do
ujemnych przyrostów produktu marginalnego w rezultacie czego produkt całkowity
zaczyna maleć,
2. Jeżeli:
MPPL  0, to
TPP  max
,
3. Produkt przeciętny i marginalny początkowo rosną a po osiągnięciu maksimum
opadają. Początkowo produkt marginalny rośnie szybciej od przeciętnego. Po
przekroczeniu punktu zrównania się obu wielkości, produkt marginalny opada szybciej
niż przeciętny,
4. Ponieważ MPPL  APPL  APPL  L , to:
MPPL  APPL zawsze, gdy produkt przeciętny rośnie oraz
MPPL  APPL zawsze, gdy produkt przeciętny maleje.
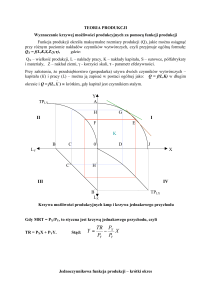
Rys. Krzywe produktu całkowitego, marginalnego i
przeciętnego
I ETAP
II ETAP
III ETAP
TPP, MPP, APP
TPP
APP
Nakład czynnika zmiennego
MPP
ETAPY PRODUKCJI
I etap:
II etap:
APPL ,
APPL  i
MPPL  0,
APPL  i
III etap: MPPL  0
TPP 
Producent maksymalizujący
produkcyjnym.
zysk
nie
będzie
wytwarzał
w
III
etapie
II. Efektywność techniczna produkcji a optimum cząstkowe producenta
IZOKWANTA
Jest to krzywa łącząca ze sobą wszystkie możliwe kombinacje czynników produkcji dające
taki sam poziom produkcji.
Kryterium efektywności technicznej będzie spełniała ta izokwanta, której nachylenie
mierzone krańcową stopą technicznej substytucji czynników produkcji
( MRTS KL  
dK
) zrówna się z relacją marginalnych produktów pracy i kapitału, czyli:
dL
MRTS KL
dTPP
dK
MPPL

 dL 
.
dL dTPP MPPK
dK
Krańcowa stopa technicznej substytucji jest stosunkiem zgodnie z którym można
zastąpić jeden czynnik produkcji drugim czynnikiem tak, aby wielkość produkcji nie
uległa zmianie.
III. Efektywność ekonomiczna produkcji a optimum cząstkowe producenta
IZOKOSZTA
Jest to linia jednakowego kosztu, czyli linia będąca zbiorem punktów będących różną
kombinacją nakładu pracy i kapitału, lecz dających taki sam poziom kosztu całkowitego,
czyli:
Y  PK K  PL L,
gdzie: Y
- poziom wydatków firmy równy jej budżetowi,
PK , PL - odpowiednio cena
jednostki kapitału i pracy, K i L – ilość zaangażowanych jednostek kapitału i pracy.
Optymalna kombinacja czynników produkcji znajduje się w punkcie styczności linii
jednakowego kosztu z możliwie najwyżej położoną izokwantą produkcji, czyli w punkcie
zrównania się współczynników kierunkowych (nachylenia) izokoszty z izokwantą. Jest to
punkt, w którym przedsiębiorstwo osiąga maksymalną wielkość produkcji przy
danym poziomie kosztów całkowitych, czyli:

MRTS KL  
dK PL

- nachylenie izokoszty,
dL PK
dK MPPL

- nachylenie izokwanty równe relacji produktów marginalnych
dL MPPK
pracy i kapitału, zatem optimum producenta:
PL
MPP L
 MRTS KL 
.
PK
MPPK
ŚCIEŻKA EKSPANSJI
Krzywa składająca się z punktów styczności izokoszt i odpowiadających im izokwant
produkcji. Punkty na ścieżce ekspansji oznaczają optymalne kombinacje czynników
odpowiadające różnym poziomom produkcji.
Ćwiczenia do zajęć 4
PYTANIA PROBLEMOWE
1. Na podstawie zależności pomiędzy izokosztą i izokwantą wyjaśnij dlaczego działanie
optymalne oznacza:
a. maksymalizację produkcji przy danym poziomie kosztów całkowitych
b. minimalizację kosztów całkowitych przy danym poziomie produkcji całkowitej.
2. Jak zmiana cen czynników produkcji wpłynie na punkt równowagi cząstkowej
producenta?
3. Jak wzrost budżetu producenta zwiększy jego możliwości maksymalizacji produkcji?
4. Dlaczego
informacje
zawarte
w
funkcji
nie
wystarczą
do
kierowania
przedsiębiorstwem?
5. Ustosunkuj się do tezy, iż większe przedsiębiorstwa zawsze mogą produkować taniej
niż małe.
6. Firma angażująca tylko jeden czynnik zmienny postanowiła zatrudnić go w takiej
ilości, aby MPP ostatniej jednostki tego czynnika był maksymalny. Czy jej decyzja
była słuszna?
7. Wykaż analogie pomiędzy teorią optimum konsumenta (teoria krzywych obojętności)
a teorią produkcji.
ZADANIA
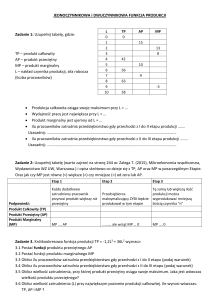
1. Wiedząc, że MRTS = -16 oblicz o ile należy zwiększyć nakład czynnika A, jeżeli ilość
czynnika B wykorzystywanego w tym procesie produkcji uległa zmniejszeniu o 4
jednostki a wielkość produkcji pozostała na tym samym poziomie.
2. Określ charakter przychodów ze skali jeżeli funkcja produkcji ma postać:
a. f ( a, b)  2ab,
b.
f (a, b)  3a 2b3 ,
c.
f ( a, b )  4a 3 b 5 .
1
3
1
2
1
2
3. Dana jest funkcja produkcji: X  100 K L . Oblicz produkt krańcowy pracy i kapitału
dla 16 jednostek pracy i 25 kapitału.
4. Przedsiębiorstwo dysponuje informacjami na temat kształtowania się produktów
marginalnych pracy i kapitału, które wynoszą odpowiednio 16 dla pracy i 36 dla
kapitału. Ceny pracy i kapitału wynoszą odpowiednio 8 i 12. Na podstawie danych
stwierdź, czy takie nakłady pracy i kapitału są optymalne. Jeżeli nie zaproponuj
zmianę zakładając, iż ceny czynników produkcji nie ulegną zmianie. Co stałoby się,
gdyby koszt kapitału wzrósł o 4 jednostki c.p.? A co by się stało z optimum
producenta, gdyby cena pracy zmalała do 4?
5. Kiedy firma zatrudniła 10 jednostkę czynnika zmiennego A, wielkość produkcji
wzrosła ze 160 do 170 jednostek. Zwiększając zatrudnienie zasobu A do 11
jednostek, produkcja całkowita wzrosła o 6 jednostek. Jest to przykładem działania:
a. prawa malejącej użyteczności krańcowej
b. malejących korzyści skali,
c. prawa malejącej produktywności krańcowej,
d. malejącej MRTS.
6.
a.
b.
c.
d.
e.
Każdy punkt izokwanty i izokoszty okreśła:
poziom TPP
TR firmy
kombinację cen czynników produkcyjnych
TC firmy
kombinację ilości wykorzystywanych w procesie produkcji czynników wytwórczych.
7. Firma produkuje 10 000 sztuk krzeseł miesięcznie angażując pracę i kapitał. Produkt
marginalny pracy wynosi 30, kapitału 15. Cena pracy wynosi 5 a kapitału 3. Aby
produkować po najniższym koszcie firma powinna:
a. nie zmieniać struktury zatrudnianych nakładów, bo jest ona najtańsza
b. zwiększyć zużycie pracy i zmniejszyć kapitału
c. zmniejszyć zużycie pracy i zmniejszyć kapitału
d. zmniejszyć zużycie pracy i zwiększyć kapitału
e. zwiększyć zużycie obu czynników.
8. Firma produkuje 200 sztuk dobra Z wykorzystując 4 zasoby według kombinacja: A =
10, B = 40, C = 20, D = 18. Ich ceny wynoszą odpowiednio: dla A – 5, B – 20, C –
10, D – 9. Czy firma produkuje po najniższym koszcie?:
a. tak
b. nie
c. zbyt mało danych.
Jeżeli dla zmienionej kombinacji, 10 : 40 : 21 : 18, produkcja wzrosła do 205 to znaczy,
że:
a. produkt marginalny A = 5,
b. produkt marginalny B = 5
c. produkt marginalny C = 5
d. produkt marginalny A i C = 5.
9. Wiedząc, że procesie produkcyjnym krańcowy produkt pracy wynosi 50 a kapitału 150
oblicz krańcową stopę technicznej substytucji kapitału przez pracę.
10. Optimum techniczne oznacza, że przedsiębiorstwo:
a. osiąga maksymalny zysk całkowity
b. maksymalizuje utarg całkowity
c. nie włoży do produkcji więcej czynnika zmiennego niż jest to konieczne do
wytworzenia danego poziomu efektu
d. nachylenie izokwanty równe jest relacji produktu krańcowego kapitału do pracy.
11. Funkcja produkcji ma postać: X  L  7 L. Oblicz produkt przeciętny i marginalny
pracy.
2