Różne warianty niedoskonałej konkurencji na rynku jednego dobra.
1. Wprowadzenie
W dotychczasowej analizie rozpatrywaliśmy przypadki, kiedy oferenci i konsumenci byli tak
rozproszeni, że żaden z nich nie mógł samodzielnie wpływać na zmiany ceny na rynku. Działania jednego
podmiotu gospodarczego nie miały żadnego wpływu na sytuację ekonomiczną pozostałych podmiotów.
Teraz natomiast będziemy interesować się sytuacjami, kiedy działania pojedynczego podmiotu mają
wpływ na sytuację ekonomiczną pozostałych, poprzez swoje działania mogą wpływać na zmiany ceny
rynkowej. Ogólnie takie rynki nazywa się rynkami o niedoskonałej konkurencji. Szczególną postacią
rynków o niedoskonałej konkurencji są rynki monopolistyczne.
2. Rynki monopolistów
Aby uprościć analizę będziemy korzystali z założeń:
1. Ze względu na ilość oferentów i nabywców przyjmujemy, że występuje albo monopol oferentów (jeden
oferent i b. wielu nabywców) albo monopol nabywców - monopson (jeden nabywca i bardzo wielu
oferentów).
2. Rynek jest homogeniczny, czyli nie istnieją żadne preferencje ze strony nabywców i oferentów w
stosunku do siebie.
3. Oferenci i nabywcy mają doskonałą przejrzystość rynku w tym sensie, że oferent monopolista zna
funkcję popytu a monopolista nabywca zna funkcję podaży. Ceny transakcji są znane wszystkim.
Zakładając racjonalne zachowanie się uczestników gry rynkowej oraz na skutek przyjęcia założeń 2
i 3 możemy stwierdzić, że w danym czasie będzie obowiązywała tylko jedna cena dla wszystkich transakcji
kupna - sprzedaży.
Prezentację zacznijmy od analizy monopolu oferenta.
3. Monopol oferenta
Rozpatrujemy teraz sytuację, gdy na danym rynku dany produkt oferuje tylko jeden producent,
którego nabywcami są bardzo liczne i rozproszone podmioty gospodarcze. Dla uwypuklenia pewnych
właściwości przyjmijmy dodatkowo, że w chwili obecnej nie ma on konkurenta i nie będzie go miał przez
dość długi okres czasu. Produkowane przez monopolistę dobro nie ma bliskich substytutów albo substytutu
są na tyle droższe, że nie stanowią dużej konkurencji dla monopolisty. Przykładami monopolistów mogą
być m.in. Zakłady Energetyczne (dostarczają prąd elektryczny do nabywców), Zakłady Gazowe
(dostarczyciel gazu sieciowego), Telekomunikacja (na rynku telefonów przewodowych), Przedsiębiorstwa
Wodociągowo-kanalizacyjne, Miejskie Przedsiębiorstwa Komunikacyjne, itp. W tych przypadkach duża
część nabywców chcąc zaspokoić określoną potrzebę mają bardzo ograniczone pole wyboru. Praktycznie
dysponują tylko alternatywą korzystać z usług monopolisty albo nie przy czym ten ostatni wybór jest
równoznaczny z rezygnacji z zaspokojenia określonej potrzeby. Np. w gospodarstwie domowym prąd
elektryczny, gaz sieciowy trudno zastąpić innymi nośnikami energii albo jest to wyraźnie droższe.
Podobnie jest w wymienionych przypadkach.
4. Funkcja cena - zbyt , przychodu i przychodu krańcowego monopolisty
Monopolista oferent zmieniając wielkość produkcji może wpływać na wysokość ceny, po
której będzie sprzedawany jego produkt. Tą zależność będziemy nazywali funkcją cena-zbyt. W
przypadku monopolisty ta funkcja cena-zbyt musi być tożsama z funkcją popytu na produkt monopolisty.
Przyjmiemy, że ta funkcja popytu jest typowa, czyli popyt maleje wraz ze wzrostem ceny, co możemy
zapisać:
x x( p )
dx
0
dp
p p( x )
dp
0
dx
gdzie: x - popyt; p - cena. W pierwszym przypadku popyt jest funkcją ceny a w drugim cena jest funkcją
popytu. W dotychczasowej analizie na rysunkach ograniczaliśmy się do prezentacji tej drugiej formy
funkcji popytu, czyli cena była funkcją popytu.
W założeniu 3 przyjęliśmy, że monopolista oferent zna funkcję popytu, co oznacza, że wie ile może
sprzedać swojego produktu po danej cenie. W tym miejscu korzystamy z przyjętego na początku rozważań
o przedsiębiorstwach uproszczenia, że produkcja wytworzona jest równa produkcji sprzedanej. Tym
samym w warunkach monopolu oferenta będziemy mogli korzystać z następującej właściwości: podaż
monopolisty jest równa popytowi na jego produkt, czyli:
y=X
Znając funkcję popytu monopolista może określić wielkość przychodu jaki osiągnie dla różnych kombinacji
wielkości produkcji i ceny. W dalszej analizie ograniczymy się do rozpatrzenia tylko najprostszego
przypadku, tzn. gdy funkcja popytu a tym samym i funkcja cena-zbyt jest prostą o ujemnym nachyleniu.
Wzór ogólny na taką prostą będzie w naszym przypadku następujący:
p = a - by
gdzie: a, b parametry funkcji większe od zera.
Aby lepiej uzmysłowić sens ekonomiczny tych parametrów rozpatrzmy prosty przykład. Powiedzmy, że
Miejskie Przedsiębiorstwo Komunikacyjne w danej miejscowości ustaliło w oparciu o odpowiednie badania
rynku, że gdyby cena biletu wynosiła 10 zł, to przewozy spadłyby do zera, gdyż np. przejazd taksówką w
granicach miasta obsługiwanego przez to MPK byłby tańszy. Z kolei wiadomo, że gdyby przejazdu
środkami publicznej komunikacji były darmowe, to dziennie korzystałoby z nich maksymalnie 100 tys.
osób. Jeżeli ilość pasażerów malałaby proporcjonalnie wraz ze wzrostem ceny biletu, to funkcja popytu na
przejazdy byłaby prostą o następującym wzorze: p = 10 - 0,0001y. Parametr a jest równy 10, natomiast
b = 0,0001. Pierwszy z nich pokazuje tzw. cenę zaporową, czyli taką cenę przy której popyt spada do zera.
Wynosi ona 10 zł. Natomiast drugi parametr b określa tempo w jakim będzie musiała maleć cena aby
przewozy wzrosły o jednego pasażera, czyli obniżka ceny o 1 gr (0,01 zł) spowoduje wzrost przewozów o
100 osób. Wróćmy ponownie do wzorów ogólnych.
W naszym przypadku funkcja przychodu monopolisty będzie wyglądała następująco:
2
E = py = y(a - by) = ay - by
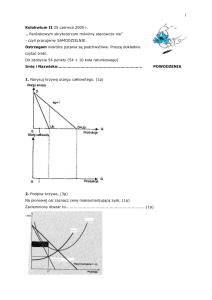
Jest to parabola ramionami zwrócona w dół o dwóch miejscach zerowych występujących dla wielkości
produkcji y1 = 0 oraz y2 = a/b oraz maksimum dla y = a/2b. Przebieg tych funkcji prezentuje rys. 1.
Funkcja przychodu
p
E
Funkcja cena - zbyt
0
a/2b
Rys. 1.
Jeżeli funkcja cena-zbyt jest prostą to łatwo jest
ustalić gdzie przychód będzie równy zero. W
pierwszym przypadku E = 0, gdyż wprawdzie cena
jest maksymalna ale y = 0 a w drugim produkcja
jest maksymalna ale z kolei cena spadła do zera i
dlatego przychód również będzie równy zero. Dla
prostoliniowych
funkcji
popytu
maksimum
przychodu będzie zawsze przypadało dla y, który
jest połową wielkości produkcji określającej pełne
nasycenie rynku, czyli gdy cena spada do zera.
W dalszej analizie wykorzystywać będziemy
pojęcie przychodu krańcowego, który można
określić jako pochodną funkcji przychodu po
y
wielkości produkcji. Aby ustalić jak będzie
a/b
wyglądała ta funkcja w analizowanym przypadku
ustalmy jej wzór. Skoro przychód jest
2
określony wzorem: E = ay - by , to przychód
krańcowy będzie równy:
2
E’ = (ay - by )’ = a - 2by
Jeżeli funkcja cena-zbyt jest prostą, to przychód krańcowy też będzie prostą. Jak łatwo zauważyć będą one
przecinały pionową oś układu współrzędnych w tym samym punkcie (na wysokości a) z tym, że przychód
krańcowy będzie 2 razy szybciej malał niż cena i dlatego przetnie poziomą oś dwa razy wcześniej niż
funkcja cena-zbyt. Prezentuje to rys. 2.
Na rys. 2 łatwo zauważyć, że przychód
p
osiąga maksimum dla tej wielkości
Funkcja przychodu
produkcji,
przy
której przychód
E
krańcowy spada do zera. Ta zależność
E'
Funkcja cena - zbyt
jest prawidłowością dla dowolnej funkcji
cena-zbyt a nie tylko dla analizowanego
przypadku. Zawsze będzie prawdziwe
twierdzenie:
jeżeli
przychód
ma
Funkcja przychodu krańcowego
maksimum to wystąpi ono dla wielkości
produkcji, gdzie przychód krańcowy jest
równy zero.
W odróżnieniu do warunków
konkurencji doskonałej w warunkach
monopolu przychód krańcowy jest
różny od ceny, w tym wypadku jest
prawie zawsze mniejszy od ceny. Są
0
a/2b
a/b
y
sobie równe tylko dla wielkości produkcji
równej zero. W warunkach gdy zmianie
Rys. 2.
wielkości produkcji towarzyszy zmiana
ceny przychód krańcowy nie pokazuje wysokości ceny po której sprzedano tą ostatnią jednostkę produkcji
ale zmianę przychodu wywołaną zmianą wielkości produkcji. Z rys. 2 możemy odczytać, że dla y = a/2b
przychód krańcowy jest równy zero., czyli wzrost sprzedaży o odpowiednio małą jednostkę produkcji nie
wywoła zmiany przychodu, nie wzrośnie on ani nie zmaleje. Może powstać pytanie jak to możliwe, skoro
wiemy, że ten produkt został sprzedany po cenie większej od zera? Cena spadnie do zera dopiero przy
produkcji dwukrotnie większej. Aby uzmysłowić sobie przyczynę tego faktu wystarczy odwołać się do
definicji przychodu. Jest on równy iloczynowi ceny i wielkości produkcji. Może więc się zdarzyć, że
iloczyn mniejszej wielkości produkcji i wyższej ceny będzie równy większej produkcji i niższej
cenie. Zilustrujmy to na prezentowanym wcześniej przykładzie. Wiemy, że przewozy wzrosną do 100 tys.
osób przy cenie równej zero, czyli maksymalny przychód to przedsiębiorstwo osiągnie przy przewozie 50
tys. osób. Aby obliczyć cenę biletu, która zapewni taki obrót, trzeba wstawić y = 50 000 do funkcji popytu
p = 10 - 0,0001y. Otrzymujemy, że cena musi być równa 5 zł. Maksymalny przychód MPK wyniesie 250
tys. zł/dziennie. Obliczmy najpierw ile wynosiłaby cena dla przewozów mniejszych i większych o jedną
osobę niż 50 000. Na tej podstawie możemy obliczyć przychody, jakie osiągnie MPK w tych przypadkach.
Wyniki obliczeń prezentuje tabela 1.
Widać, że wzrost przewozów o 2 osoby z poziomu 49 999 do 50
Ilość
Cena
Przychód
001 nie wpłynie na zmianę przychodu, mimo że cena jest większa
pasażerów biletu
49 999
5,0001 zł 249 999,99 zł od zera. W przypadku prostoliniowej funkcji popytu wzrost
50 000
5 zł
250 000,00 zł produkcji o jednostkę wymaga obniżenia ceny o tą samą kwotę,
50 001
4,9999 zł 249 999,99 zł czyli cena maleje wraz ze wzrostem sprzedaży w stałym tempie.
Natomiast zwiększenie produkcji o tą samą jednostkę oznacza, że
produkcja rośnie coraz wolniej wraz z jej wzrostem. Jeżeli zwiększymy sprzedaż o 1 sztukę z poziomu 1 do
2, to sprzedaż rośnie w tempie 1, czyli o 100%, natomiast gdy zwiększymy produkcję o tą samą jednostkę
z poziomu 100 do 101, to y rośnie w tempie 0,01, czyli o 1%.
Przychód monopolisty rośnie tak długo dopóki cena wolniej spada niż rośnie sprzedaż. Jeżeli
sprzedaż rośnie wolniej niż spada cena, to przychód monopolisty będzie malał. Maksymalny przychód
osiągnie, gdy cena maleje w tym samym tempie jak rośnie sprzedaż.
5. Optymalna wielkość produkcji i cena oferenta monopolisty
W odróżnieniu od wcześniej rozpatrywanego przypadku producenta działającego w warunkach
doskonałej konkurencji teraz monopolista wybierając najlepszą dla siebie wielkość produkcji, czyli taką
która maksymalizuje jego zysk, automatycznie ustala cenę na swój produkt.
Koszty i przychód możemy zapisać jako funkcje wielkości produkcji y. Maksimum zysku jest osiągane, gdy
jest spełniony warunek konieczny:
Z’ = E’ - Kc’ = 0
czyli:
E’ = Kc’
Warunek wystarczający jest spełniony, jeżeli:
Z’’ < 0
czyli:
E’’ < Kc’’
Oznacza to, że nachylenie kosztów krańcowych musi być większe niż nachylenie krzywej
przychodu krańcowego. W związku z tym, że w typowych warunkach E’’ jest mniejsze od zera, gdyż
przychód krańcowy jest funkcją malejącą, to maksimum zysku może wystąpić nie tylko wtedy, gdy
przychód krańcowy przecina się z kosztami krańcowymi na rosnącej gałęzi Kc’ ale również na malejącej
gałęzi, z tym że spadek kosztów krańcowych musi być wolniejszy niż spadek przychodu krańcowego.
Jeżeli funkcja zysku monopolisty ma minimum, to wystąpi ono dla tej wielkości produkcji dla której
są spełnione następujące warunki:
E’ = Kc
E’’ > Kc’’
Oznacza to, że minimum zysku monopolista osiągnie dla tej wielkości produkcji, przy której przychód
krańcowy przecina się z kosztami krańcowymi i dodatkowo koszty krańcowe szybciej maleją niż przychód
krańcowy.
Jeżeli funkcja kosztów monopolisty przebiega typowo (tak jak to jest przedstawione na górnej
części rys. 3a) a funkcja popytu (cena - zbyt) jest prostą o ujemnym nachyleniu, to na rysunku
przedstawia się to następująco:
Na wstępie należy powiedzieć, że
przedstawiony na rys. 3a przypadek
nie jest ogólny, gdyż jest również
Kc
możliwe, że funkcje przychodu i
kosztów całkowitych nie będą się
Z
przecinały,
co
oznaczałoby,
że
F
G
D’
monopolista będzie ponosił straty dla
E
każdej
wielkości
produkcji.
Taki
przypadek jest rzadszy, dlatego analizę
C
B
ograniczymy
do
przedstawionego
D
przypadku. Aby możliwie poszerzyć
wnioski przyjęto, chociaż nie jest to
A
nieuchronne, że dla wielkości produkcji
bliskich zera do punktu A koszty
całkowite rosną szybciej niż przychód,
A’
co oznacza, że na odcinku 0A krzywa
Kc’ jest bardziej stroma niż krzywa E na
odcinku 0A’. Tym samym początkowa
y
strata równa kosztom stałym rośnie do
wielkości produkcji odpowiadającej
Z
punktom A i A’. Jeżeli dla większych
wielkości produkcji koszty całkowite
rosną wolniej niż przychód, to strata
p
musi się stopniowo zmniejszać. Tym
Kc’
Kcp
samym funkcja zysku dla tej wielkości
E’
produkcji osiąga minimum. Oznacza to
Kc’
również, że przy tej wielkości produkcji
muszą się przeciąć funkcje przychodu
Kcp
krańcowego i kosztów krańcowych H
p*
patrz dolny układ współrzędnych.
Skoro straty po przekroczeniu
wielkości produkcji odpowiadającej
punktowi A będą malały, to zmaleją do
zera
przy
wielkości
produkcji
odpowiadającej punktowi B. Tam
L
muszą się przeciąć funkcje ceny i
K
przeciętnych kosztów całkowitych E’
zob. dolny układ współrzędnych.
Punkt C jest punktem przegięcia
funkcji kosztów całkowitych i tym
0
samym najbardziej płaskim odcinkiem
y*
y
tej krzywej, czyli koszty krańcowe dla
Rys. 3a.
tej wielkości produkcji muszą osiągać
minimum.
Nachylenie krzywych Kc i E w punktach D i D’ jest takie samo, co oznacza, że dla tej wielkości
ponownie występuje równość kosztów krańcowych i przychodu krańcowego (te funkcje się tam przecinają
- zob. dolny układ współrzędnych). W odróżnieniu od poprzedniego, który wskazywał minimum funkcji
zysku, teraz mamy do czynienia z jej maksimum, gdyż koszty krańcowe już rosną a przychód krańcowy
nadal maleje, czyli musi zachodzić nierówność E’’ < Kc’’.
W punkcie F przychód osiąga maksimum, czyli dla tej wielkości produkcji przychód krańcowy musi
być równy zero. Musi to być połowa wielkości produkcji, przy której przychód spada do zera.
Punkt G, gdzie przecinają się funkcje przychodu i kosztów całkowitych zysk jest równy zero, co
oznacza, że przy tej wielkości produkcji muszą się ze sobą przecinać prosta ceny z krzywą przeciętnych
kosztów całkowitych.
Dla tej wielkości produkcji, dla której przychód spada do zera prosta cena musi być równa zero.
Kc
E
Optymalna wielkość produkcji, czyli taka która maksymalizuje zysk monopolisty wynosi w
przedstawionym przypadku y*. Tej wielkości towarzyszy automatycznie ustanowienie przez monopolistę
ceny p*. Korzystając z dolnego układu współrzędnych rys. 3 możemy powtórzyć, że maksimum zysku
wystąpi dla tej wielkości produkcji, przy której koszty krańcowe przetną się z przychodem
krańcowym i nachylenie tej pierwszej funkcji będzie większe niż drugiej. Optymalną cenę
znajdujemy na funkcji cena-zbyt dokładnie nad y*.
Wielkość zysku jaki osiągnie monopolista możemy pokazać jako pole odpowiedniego prostokąta.
Długość odcinka HK pokazuje wysokość zysku przeciętnego a odcinek 0y* wielkość produkcji. Tym samym
pole prostokąta którego wierzchołki wyznaczają punkty p*HKL pokazują wielkość maksymalnego zysku.
Do tego wniosku można dojść zauważając, że wielkość przychodu z definicji jest równa iloczynowi
ceny i wielkości produkcji. Mnożąc p* przez y* otrzymamy pole prostokąta o wierzchołkach p*Hy*0.
Koszty całkowite możemy wyliczyć mnożąc przeciętne koszty całkowite przez wielkość produkcji. Tym
samym wysokość kosztów całkowitych w optymalnym punkcie monopolisty będzie obrazowana przez pole
prostokąta o wierzchołkach LKy*0. Zysk jako różnica przychodu i kosztów całkowitych będzie więc
ukazany jako pole prostokąta p*HKL.
6. Porównanie doskonałej konkurencji i monopolu oferenta
Na tym etapie analizy możemy dokonać pierwszych porównań z wnioskami otrzymanymi przy
okazji prezentacji rynku o doskonałej konkurencji w krótkim okresie czasu. Warto zauważyć, że o ile w
doskonałej konkurencji optymalna wielkość produkcji przy cenach wyższych niż próg zysku zawsze
wypadała dla większych wielkości niż te, przy których producent osiągał minimalne przeciętne koszty
całkowite. Teraz w warunkach monopolu jest możliwe, że y* wypadnie dla wielkości produkcji mniejszych
niż minimum Kcp.
W warunkach monopolu nie ma odpowiednika ceny progu zysku, czy ceny progu zamknięcia jak w
doskonałej konkurencji. Wynika, to z tego, że cena w monopolu nie jest parametrem do wysokości którego
oferent musi się dostosować ale jest taką samą zmienną jak wielkość produkcji.
W warunkach monopolu nie można też mówić o indywidualnej funkcji podaży, tak jak to robiliśmy
w doskonałej konkurencji. Przypomnijmy, że indywidualna funkcja podaży była wtedy tym fragmentem
krzywej kosztów krańcowych, który leżał powyżej punktu przecięcia z funkcją przeciętnych kosztów
zmiennych. Teraz w monopolu nie można mówić o funkcji podaży monopolisty. Pokażemy to na prostym
przykładzie, który prezentuje rys. 4.
W warunkach monopolu oferowana przez monopolistę ilość
p
podaży zależy nie tylko od przebiegu jego funkcji kosztów
Kc’
nowa funkcja cena-zbyt
krańcowych ale również od przebiegu funkcji cena - zbyt.
E’
Na rys. 4 przedstawiono sytuację, kiedy monopoliście
nowy przychód krańcowy
udało się tak zmienić nastawienie swoich odbiorców, że na
p2*
podwyżki cen będą reagować mniejszą redukcją popytu.
Jak widać może więc się zdarzyć, że w wyniku tych działań
stara funkcja cena-zbyt
monopolista dążąc do maksymalizacji swojego zysku
p1*
będzie mógł podnieść cenę z poziomu p1* do p2* bez
stary przychód krańcowy
zmiany wielkości produkcji y*.
Ten przypadek oznacza, że w monopolu nie
możemy jednoznacznie przypisać danej wielkości
y
y*
produkcji tylko jednej ceny, co jest warunkiem koniecznym
aby można było mówić o funkcji podaży.
Rys. 4.
Dla
uzupełnienia
rozpatrywanego
ostatnio
przypadku warto zauważyć, że monopolista poprzez odpowiednie działania może się również doprowadzić
do tego, że będzie mógł zwiększyć sprzedaż bez obniżania ceny.
Warto w tym miejscu wspomnieć, co może być powodem tego typu przesunięć funkcji popytu jak to
zostało ukazane na rys. 4. Nabywcy będą na podwyżki cen tego wyroby reagowali mniejszą niż poprzednio
obniżką popytu, wtedy gdy w ich ocenie produkt wytwarzany przez monopolistę jest im bardziej potrzebny
niż poprzednio i jednocześnie trudniej go zastąpić innym. Im mniej substytutów ma dane dobro i im
ważniejszą potrzebę ono zaspakaja tym nabywcy będą wolniej rezygnowali z jego zakupów w przypadku
wzrostu jego ceny. Taki efekt monopolista może osiągnąć albo modyfikując swój produkt, tak że lepiej
zaspakaja on potrzeby nabywców albo modyfikując wyobrażenia klientów o swoim produkcie poprzez np.
odpowiednią kampanię reklamową albo - co czyni się najczęściej - wykorzystując oba narzędzia. Badaniem
tego typu działań zajmuję się m.in marketing.
Doskonałą konkurencję i monopol można porównać również ze względu na optymalną wielkość
produkcji przedsiębiorstwa i cenę jaka ustali się na rynku. W tym celu rozważmy dwie sytuacje, które różni
jedynie forma rynku natomiast wszystkie inne elementy wpływające na wielkość produkcji i cenę będą
takie same. W tym celu rozważmy sytuację pierwszą, kiedy dany produkt jest dostarczany na rynek przez
tylko jednego producenta, co prezentuje rys. 5.
Zgodnie z wcześniejszymi ustaleniami możemy powiedzieć, że monopolista ustali swoją wielkość produkcji
Funkcja cena-zbyt monopolisty na poziomie y*m i tym samym na rynku będzie obowiązywała cena
p,
lub funkcja popytu
E’,
p*m, gdyż wtedy przychód krańcowy będzie równy kosztom
Kc’
krańcowym i monopolista osiągnie maksymalny zysk.
Wyobraźmy sobie, że monopolistę zastąpiła teraz bardzo
Kc’
liczna grupa drobnych producentów, których zsumowana funkcja
p*m
kosztów całkowitych pokrywa się z funkcją kosztów monopolisty.
Wtedy koszty krańcowe monopolisty, przedstawione na rys. 5 będą
ilustracją przebiegu zagregowanej funkcji kosztów krańcowych
p*dk
pojedynczych producentów. Z wcześniejszych ustaleń wiemy, że
odpowiedni fragment rosnącej gałęzi tej funkcji w warunkach
doskonałej konkurencji jest funkcją podaży. Z kolei funkcja
E’
cena-zbyt monopolisty to nic innego jak funkcja popytu. Tym samym
możemy stwierdzić, że równowaga na tym rynku w warunkach
y*m
y*dk
y
konkurencji doskonałej ustali się na poziomie y*dk i przy cenie p*dk.
Porównując je z y*m i p*m stwierdzimy, że w warunkach monopolu
Rys. 5.
podaż zawsze będzie mniejsza a cena wyższa niż w doskonałej
konkurencji. To twierdzenie warunków ceteris paribus, czyli gdy wszystkie pozostałe czynniki wpływające
na optymalną wielkość produkcji i cenę rynkową są takie same w obu przypadkach.
Jednakże koszty krańcowe monopolisty oferenta Km’, dzięki temu, ze jest on na ogół dużym
przedsiębiorstwem mogącym wykorzystać tzw. efekt skali, czy też prowadzić owocne badania nad nowymi
technologiami, mogą okazać się niższe niż zagregowane koszty drobnych oferentów wytwarzających tę
samą ilość produkcji Kk’=S. W skrajnym przypadku, choć w praktyce niezmiernie rzadko, może zdarzyć się
sytuacja taka jak na rys. 6., który pokazuje, iż cena na rynku monopolu oferenta może być nawet niższa
niż na rynku konkurencji doskonałej. Może to jednak mieć miejsce np. przy wytwarzaniu produktu przez
monopolistę w warunkach nieważkości czy przy zastosowaniu wymagających wielu badań metod
inżynierii genetycznej.
p
Kk’=S
p*k
p*m
Km
’
p(y)
E’
y*k y*m
rys. 6
y