Sprawność maszyn cieplnych

Sprawność maszyn cieplnych.
Z II zasady termodynamiki wynika:
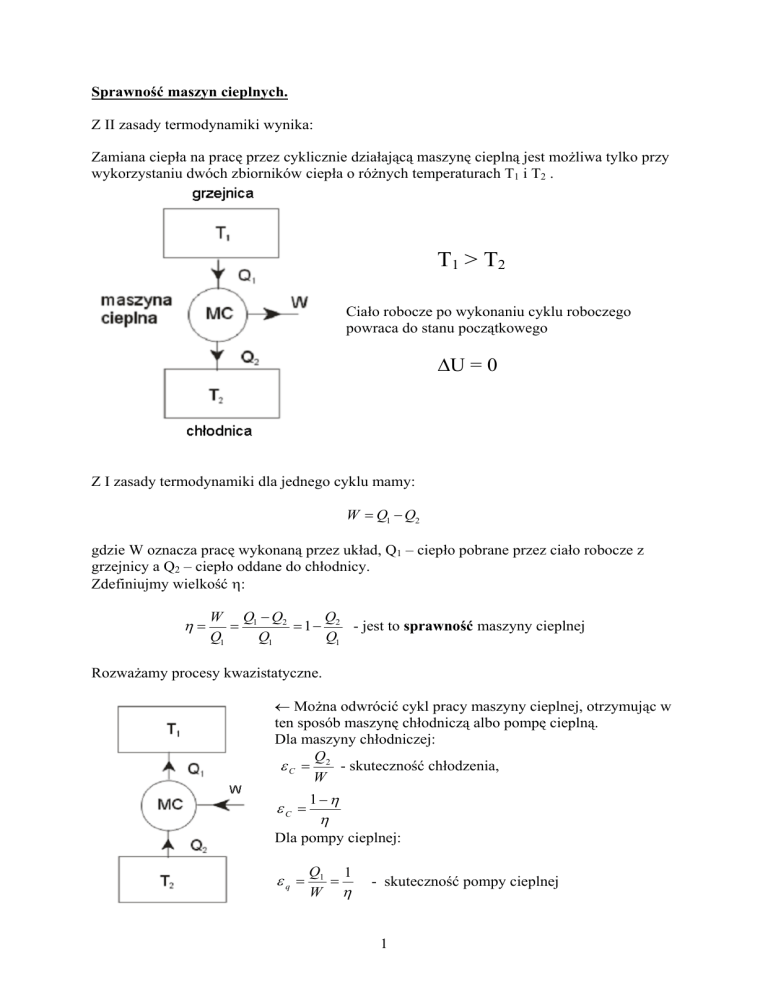
Zamiana ciepła na pracę przez cyklicznie działającą maszynę cieplną jest możliwa tylko przy
wykorzystaniu dwóch zbiorników ciepła o różnych temperaturach T1 i T2 .
T1 > T2
Ciało robocze po wykonaniu cyklu roboczego
powraca do stanu początkowego
∆U = 0
Z I zasady termodynamiki dla jednego cyklu mamy:
W = Q1 − Q2
gdzie W oznacza pracę wykonaną przez układ, Q1 – ciepło pobrane przez ciało robocze z
grzejnicy a Q2 – ciepło oddane do chłodnicy.
Zdefiniujmy wielkość η:
η=
W Q1 − Q2
Q
=
= 1 − 2 - jest to sprawność maszyny cieplnej
Q1
Q1
Q1
Rozważamy procesy kwazistatyczne.
← Można odwrócić cykl pracy maszyny cieplnej, otrzymując w
ten sposób maszynę chłodniczą albo pompę cieplną.
Dla maszyny chłodniczej:
Q
ε C = 2 - skuteczność chłodzenia,
W
εC =
1−η
η
Dla pompy cieplnej:
εq =
Q1 1
=
W η
- skuteczność pompy cieplnej
1
Twierdzenie Carnota:
Sprawność dowolnego cyklu odwracalnego zależy tylko od temperatur T1 i T2 ,
a nie zależy od ciała roboczego ani od konstrukcji maszyny.
Sprzęgnijmy układy tak, aby W’=W.
Załóżmy η’>η :
W′ W
>
⇒ Q1′ < Q1 ⇒ Q2′ < Q2
Q1′ Q1
Praca wykonana przez układ W ′ − W = 0 . Jedynym skutkiem działania tego układu byłoby
przenoszenie ciepła Q2 − Q2′ = Q1 − Q1′ > 0 z chłodnicy do grzejnicy. Ale to przeczy II
zasadzie termodynamiki. Podobne rozważania można wykonać dla η’<η, co również
prowadzi do sprzeczności.
Pozostaje zatem tylko możliwość η’=η !
Absolutna skala temperatur.
Kelvin wprowadził absolutną skalę temperatur. Rozważmy sytuację jak na rysunku poniżej.
„t” oznacza tu temperaturę nieskalowaną.
2
Q
Q2
= 1 − η , z twierdzenia Carnota: 2 = f (t1 , t 2 )
Q1
Q1
Łączny efekt działania cykli K’ i K” jest taki sam jak cyklu K .
Q3
Q
= f (t1 , t 3 ) , 2 = f (t 3 , t 2 )
Q1
Q3
Q2 Q2 / Q1 f (t1 , t 2 )
=
=
Q3 Q 3 / Q1 f (t1 , t 3 )
⇓
f (t 3 , t 2 ) =
f (t1 , t 2 )
f (t1 , t 3 )
Sprawność cyklu K” nie zależy od t1 , a zatem:
g (t 2 )
g (t 3 )
Możemy teraz ustalić absolutną skalę temperatury przez warunek :
f (t 3 , t 2 ) =
g (t ) = cT
gdzie T – temperatura absolutna.
Tak więc:
Q2 T2
=
Q3 T3
Wtedy sprawność maszyny cieplnej możemy napisać jako:
η = 1−
Q2
T
= 1− 2
Q1
T1
- wzór Kelvina
Przypisanie wybranemu punktowi określonej wartości temperatury T definiuje całą skalę:
T′ =
Q′
T
Q
3
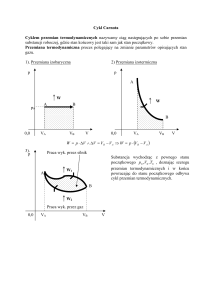
Cykl Carnota.
W rzeczywistości pomiar nie jest możliwy, gdyż nie dysponujemy odwracalnymi maszynami
cieplnymi, możemy jednak rozważyć cykl Carnota, gdzie ciałem roboczym jest gaz
doskonały.
A→ B : rozprężamy izotermicznie gaz w temperaturze T1 od objętości V1 do V2 , dostarczając
ciepło Q1 :
UA = UB,
∆U = 0
Praca wykonana przez gaz jest równa dostarczonemu ciepłu:
W AB = Q1 = RT ln
V2
V1
B→C : adiabatyczne rozprężanie gazu:
T1V2γ −1 = T2V3γ −1 (‘)
Gaz wykonuje pracę kosztem swojej energii wewnętrznej:
∆U=UC – UB
C→D : izotermiczne sprężanie gazu. Praca zewnętrzna zużyta na sprężenie gazu równa się
ciepłu oddanemu przez gaz do chłodnicy:
V 
WCD = Q2 = RT2  4 
 V3 
D→A : sprężanie adiabatyczne gazu:
T2 Ê T1 , ∆U = UA – UD >0
4
T1V1γ −1 = T2V 4γ −1 (‘‘)
z (‘) i (‘‘) →
V1 V4
=
V 2 V3
Tak więc :
V
WCD = Q2 = RT2 ln 1
 V2



Sprawność cyklu
η = 1−
Q2 (ukl )
T
= 1 − 2 (‘‘‘)
Q1 ( zew)
T1
Sprawność cyklu Carnota jest oczywiście identyczna ze sprawnością wynikającą ze wzoru
Kelvina.
Skala termometru gazowego z gazem doskonałym jest identyczna ze skalą temperatury
bezwzględnej Kelvina.
Absolutna skala temperatur:
Wybrany punkt – punkt potrójny wody:
273,16 0K
Skala Celsjusza: t = T – T0 [°C], T0 = 273,15 0K
T0 jest zdefiniowana jako temperatura topnienia lodu przy ciśnieniu normalnym.
Cykl Otto.
5
I suw: A→B - mieszanka zasysana jest do wnętrza silnika,
II suw: B→C - adiabatyczne sprężanie mieszanki od objętości V1 do V2,
III suw: C→D→E→B - zapłon mieszanki, wydzielanie ciepła następuje praktycznie w
stałej objętości a następnie spaliny rozprężają się adiabatycznie
do objętości V1, otwarcie zaworu wylotowego,
IV suw: B→A - usunięcie spalin na zewnątrz.
Jeśli zastosujemy tutaj wzory opisujące odwracalne przemiany izoparametryczne, to mamy:
η =1−
gdzie r =
(V1
1
V2 )
γ −1
=1−
1
r
γ −1
V1
jest to stopień sprężania.
V2
Cykl Diesla.
Teoretyczna sprawność takiego procesu:
γ
 V3 
V
  −  2
V
1 V
η =1−  1   1
γ  V3   V 2
  − 
 V1   V1
6






γ
Dla rzeczywistych silników ta sprawność jest mniejsza, gdyż zachodzące w nich procesy są
nieodwracalne:
T
η nieodwr < 1 − 2 = η odwr
T1
Demonstracja: ptak pijący wodę jako przykład silnika cieplnego.
7