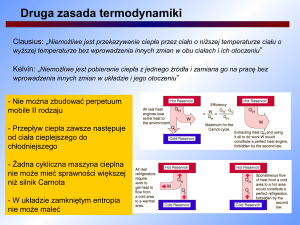
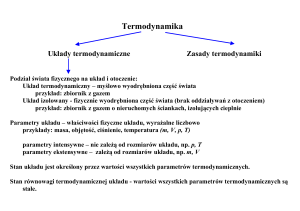
Fizyka statystyczna a termodynamika
fenomenologiczna
Fizyka statystyczna (teoria kinetyczno-cząsteczkowa) i
termodynamika - dział fizyki zajmujący się badaniem energetycznych
efektów wszelkich przemian fizycznych i chemicznych, które wpływają
na zmiany energii wewnętrznej analizowanych układów.
Termodynamika zajmuje się nie tylko przemianami cieplnymi, lecz
także efektami energetycznymi reakcji chemicznych, przemian z
udziałem jonów, przemianami fazowymi, a nawet przemianami
jądrowymi.
Termodynamika fenomenologiczna - bada wspomniane zjawiska z punktu
widzenia energetycznych efektów makroskopowych, nie wnikając w
naturę tych przemian na poziomie pojedynczych cząsteczek.
Zaniedbuje budowę mikroskopową ciał.
Fizyka statystyczna - próbuje wyjaśniać prawa i zjawiska badane
przez termodynamikę klasyczną na poziomie rozważań
cząsteczkowych. Zajmuje się badaniem parametrów mikroskopowych
układu, poszukiwaniem ich wartości średnich oraz powiązaniem tych
wartości średnich z parametrami makroskopowymi opisującymi układ
jako całość.
Dla dowolnego układu wielkości makroskopowe i mikroskopowe są ze
sobą związane – stanowią inny sposób opisu układu.
1 cm3 gazu
1019 cząstek.
Równanie Newtona dla i-tej cząstki układu N cząstek
2
d ri
mi 2
dt
Fi ( z )
Suma sił
zewnętrznych
Fij
i, j 1, 2, N
i , j (i j )
Siła z jaką j-ta
cząstka działa na i-tą
Siły wewnętrzne są siłami newtonowskimi
Dla układu N cząstek otrzymujemy układ N równań - trudny do
rozwiązania numerycznego a niemożliwy do rozwiązania analitycznego.
Opis metodami statystycznymi
Stan układu (gazu) jako całości jest opisany przez:
• temperaturę,
• ciśnienie
parametry makroskopowe
• objętość.
Parametry makroskopowe są związane ze średnimi wartościami
parametrów opisujących stan poszczególnych cząstek
• średnia prędkość
• średni kwadrat prędkości
• średnia energia kinetyczna
parametry mikroskopowe
• masa cząstki
• pęd cząstki
• położenie cząstki
Masa i rozmiary cząstek
Masa atomowa danego pierwiastka Ar – stosunek masy atomu
tego pierwiastka do masy 1
atomu węgla
12
C
12
Masa cząsteczkowa Mr – stosunek masy cząsteczki danej
substancji do masy 1
atomu węgla
12
C
12
Atomowa jednostka masy (1 u) – 1 masy atomu węgla
12
12
C
1 mol (gramocząsteczka) – ilość substancji zawierająca taką samą
liczbę atomów (cząsteczek) co 0.012 kg izotopu węgla 12C
Liczba Avogadra – liczba atomów (cząsteczek) w 1 molu substancji
N A 6.022 10 23 mol -1
M
mu
N A Ar
mu
0.012
kg
mol
6.022 10 23 12
1
mol
Masa dowolnego atomu
1.66 1027 kg Ar
masa dowolnej cząsteczki
1.66 1027 kg M r
1.66 10 27 kg
wodór
Rozmiary cząsteczek – oszacowanie
1 mol wody
zajmuje objętość
H 2 0
2 1 16 18g
sarin
18 106 m3
Na 1 cząsteczkę przypada objętość
18 106
3
30
3
V
m
30
10
m
6.022 10 23
V r3
r 3 30 1030 3 1010 m
Stan układu termodynamicznego
Układ termodynamiczny
wyodrębniona część świata
stanowiąca przedmiot badań.
Otoczenie
wszystko to co nie należy do układu.
Układ izolowany
układ nie oddziałujący z
otoczeniem.
Układ
termodynamiczny
otoczenie
Stan układu termodynamicznego opisują parametry:
• wewnętrzne – uśrednione wielkości mikroskopowe i powiązane z nimi
wielkości makroskopowe,
• zewnętrzne – siły zewnętrzne działające na układ, kształt, położenie
układu.
Parametry wewnętrzne możemy podzielić na:
• ekstensywne – zależne od masy układu (objętość, energia, entropia)
• intensywne – niezależne od masy układu (temperatura, ciśnienie,
gęstość).
m, V, U, S
m, V, U, S
T, p,
T, p,
mc=6m, Vc=6V, Uc=6U, Sc=6S
ekstensywne
m, V, U, S
T, p,
m, V, U, S
m, V, U, S
m, V, U, S
T, p,
T, p,
T, p,
T, p, - jednakowe
dla całego układu
intensywne
Układy
termodynamiczne
Otwarte
wymieniające masę
lub energię z
otoczeniem
Zamknięte (izolowane)
nie wymieniające masy
ani energii z
otoczeniem
układ zamknięty
układ otwarty
woda
ścianki adiabatyczne
Parametry stanu układu
ciśnienie
objętość
temperatura
ilość moli (masa)
p
V
T
n (m)
Parametry te mierzymy odpowiednimi przyrządami
Stan nierównowagowy – jeśli jeden z parametrów
opisujących stan układu, np. temperatura, przyjmuje w
różnych punktach różne wartości.
Jeśli układ odizolujemy od innych – temperatura
zacznie się wyrównywać i przyjmie jednakową wartość
we wszystkich punktach – układ osiągnie stan
równowagi.
stan
nierównowagowy
relaksacja
stan
równowagi
Czas relaksacji – czas, po którym dany parametr maleje
e-krotnie.
Stan równowagi – wszystkie parametry mają określone
wartości przy jednakowych warunkach zewnętrznych.
Każda przemiana – przejście ze stanu (1) do stanu (2) –
narusza stan równowagi.
stan 1
p1 , V1 ,T1, m
stan 2
p2 ,V2 ,T2, m
Proces kwazistatyczny – proces odbywający się z
nieskończenie małą prędkością - układ w każdej chwili
jest w stanie równowagi.
Przemiana składająca się z kolejnych stanów równowagi –
przemiana równowagowa (kwazistatyczna).
Niech podczas przemiany pewien
A
parametr, np. A ulega zmianie o
A w czasie . Jeśli
dA
A
dt
V
to proces jest kwazistatyczny.
Proces kwazistatyczny jest procesem odwracalnym – po
powrocie ze stanu końcowego do początkowego otoczenie
układu również znajduje się w stanie początkowym.
p
Proces niekwazistatyczny – jest procesem nieodwracalnym.
p
V
Przemiana kołowa (cykl) – przemiana, w której układ po
przejściu szeregu stanów powraca do stanu
początkowego.
Przykładowy cykl
p
1
izotermiczna
2
izochoryczna
3
adiabatyczna
V
Temperatura
Jeżeli dwa układy znajdują się w stanie równowagi
termodynamicznej z trzecim układem, to muszą znajdować
się w stanie równowagi względem siebie.
Zerowa zasada termodynamiki
Jeśli układy A i B mogące ze sobą wymieniać ciepło są ze sobą w
równowadze termodynamicznej, i to samo jest prawdą dla układów B
i C, to układy A i C również są ze sobą w równowadze. Przez
równowagę termodynamiczną rozumiemy stan, który w danych
warunkach układ osiąga i już go nie zmienia.
Z zerowej zasady wynika istnienie temperatury. Istnieje mianowicie
taka wielkość fizyczna , która jest równa dla układów A i B,
będących ze sobą w równowadze termodynamicznej
f (T )
W szczególności
T
temperatura bezwzględna
• Temperatura bezwzględna każdego zwyczajnego układu
T > 0,
• Średnia energia kinetyczna E T,
• Układ o temperaturze bezwzględnej wyższej będzie
oddawał ciepło układowi o temperaturze bezwzględnej
niższej
Pomiar temperatury
Termometr – dowolny układ makroskopowy do mierzenia
temperatury:
• parametr termometryczny układu zmienia się
dostatecznie szybko, gdy układ traci lub pobiera energię
• jest znacznie mniejszy niż układy, które badamy przy
jego pomocy.
termometr
Parametr termometryczny X
cieczowy – rtęć lub alkohol
wysokość słupa cieczy
gazowy o stałej objętości
ciśnienie
gazowy o stałym ciśnieniu
objętość
oporowy
oporność
termopara
siła termoelektryczna
itd
Dwa układy pozostaną w równowadze po ich skontaktowaniu
termicznym wtedy i tylko wtedy, gdy ich temperatury względem
tego samego termometru są równe.
oporność metali
l
R
S
oporność półprzewodnika
Załóżmy liniową zależność parametru termometrycznego
od temperatury
co oznacza, że
T ( x) ax
T ( x1 ) ax1
T ( x2 ) ax2
T ( x1 ) x1
T ( x2 ) x2
Do wyskalowania termometru przyjęto punkt potrójny wody
– lód, woda i para wodna współistnieją w stanie równowagi –
ciśnienie 611.2 Pa, temperatura (przyjęta arbitralnie) 0ºC =
273.15 K
T ( x)
x
T ( xtr ) xtr
x
x
T ( x) T ( xtr )
273.15 K
xtr
xtr
Skale temperatur
Skala Celsjusza (1742 r)
dwa charakterystyczne punkty temperatury topnienie śniegu i wrzenie wody.
Jednostką temperatury jest stopień - °C
0°C
temperatura topnienia lodu,
100°C
temperatury wrzenia wody
w warunkach normalnego ciśnienia atmosferycznego.
x x0
t C 100
x100 x0
Skala Kelvina
273.15 K
temperatura topnienia lodu,
373.15 K
temperatury wrzenia wody
x
T ( K ) 273.15 K
xtr
Niektóre temperatury [K]
Helowa reakcja termojądrowa
108
Wnętrze Słońca
107
Powierzchnia Słońca
Topnienie wolframu
6103
3,6103
Topnienie ołowiu
6102
Zamarzanie wody
2,7102
Skraplanie tlenu
9101
Skraplanie wodoru
2101
Skraplanie helu (4He)
Skraplanie helu (3He) przy najniższym osiągalnym
ciśnieniu
4,2
310-1
Adiabatyczne rozmagnesowanie soli
paramagnetycznych
10-3
Adiabatyczne rozmagnesowanie jąder atomowych
10-6
Zmiany stanu skupienia
cp
Q
m T
Rozszerzalność cieplna
Amplituda drgań ~ 10-9 cm, częstość ~ 1013 Hz. Przy
wzroście temperatury rośnie odległość między atomami.
F
dU
dr
Rozszerzalność cieplna odpowiada wzrostowi średnich odległości między
atomami ciała.
r < re – siły odpychające i energia potencjalna szybko rośnie
r > re – siły przyciągania nieco słabsze, energia potencjalna rośnie
wolniej
Rozszerzalność jest wynikiem asymetrii krzywej energii potencjalnej.
Zmiana wymiaru liniowego ciała – rozszerzalność
liniowa
·10-6 [K-1]
aluminium
23
arsen
6
kobalt
12.6
żelazo
12.5
potas
84
srebro
20
porcelana
4
stal
13
diament
1
l l0 t
lt l0 l0 t
lt l0 1 t
długość w
temperaturze t
długość w
temperaturze t =0ºC
Zmiana objętości ciała – rozszerzalność objętościowa.
Dla ciał izotropowych współczynnik rozszerzalności
objętościowej
3
Vt V0 1 t
objętość w temperaturze t
objętość w temperaturze t =0ºC
Kalorymetria
Do ogrzania masy m danej substancji o T należy dostarczyć
Q mcT
ciepła.
Ciepło właściwe
1 Q
c
m T
w granicy
1 dQ
c
m dT
ilość ciepła potrzebna do podgrzania 1kg danej substancji o 1K.
Pojemność cieplna
C mc
Jeśli ciepło właściwe jest funkcją temperatury to
(zazwyczaj niewiele zależy od temperatury)
T2
Q m c(T )dT
T1
Ciepło właściwe
J/(kgK)
Ciepło
topnienia J/kg
Ciepło parowania
J/kg
aluminium
895
32·104
miedź
395
22·104
platyna
120
10.5·104
woda
4187
33.4·104
22.6·104
benzen
1710
12.7·104
39.4·104
rtęć
138.5
11.7·103
27·104
Ciepło przemiany fazowej – ciepło utajone
Q mc
topnienie (krzepnięcie)
parowanie (skraplanie)
Równanie stanu gazu doskonałego
Gaz doskonały:
• cząsteczki traktujemy jak punkty materialne – zaniedbujemy
objętość własną cząsteczek gazu
• cząsteczki podlegają prawom mechaniki Newtona
• cząsteczki zdarzają się ze sobą sprężyście, wymieniają pęd bez
strat energii
• poza momentami zderzeń cząsteczki nie oddziałują ze sobą, a czas
trwania tych zderzeń jest pomijalnie mały – krótkozasięgowe siły
oddziaływania międzycząsteczkowego - pomiędzy zderzeniami
cząsteczki poruszają się ruchem jednostajnym prostoliniowym.
Gazy silnie rozrzedzone można traktować jak gazy doskonałe.
Stan danej masy gazu opisują 3 parametry: p, V, T
Dla warunków normalnych
p0 1.013 10 5 Pa
T0 273 K
V0 22.4 10 3 m 3
n 1 mol
pV
const
T
p0V0 1.013 105 22.4 103 J
J
8.31
T0
273
K
K
uniwersalna stała gazowa R
równanie Clapeyrona
pV nRT
n
m
M
liczba moli
Przemiany gazowe – zmiana stanu układu
stan 1
p1 , V1 ,T1, m
przemiana
stan 2
p2 ,V2 ,T2, m
T = const – przemiana izotermiczna
1
pV const
m
pV
RT
M
prawo Boyle’a – Mariotte’a
ciśnienie p
izotermy
p1V1 p2V2
Robert Boyle (1627 - 1691)
0
0
objętość V
T1 > T2 >T3
Edme Mariotte (1620-1684)
p = const – przemiana izobaryczna
2
m
pV
RT
M
V
const
T
prawo Gay - Lussaca
objętość
p1 < p2 <p3
JOSEPH LOUIS GAY-LUSSAC
(1778-1850)
0
0
temperatura
VT
V 0
T0
V V0 1 t
Dla gazów – niezależnie od od wartości ciśnienia zewnętrznego –
ogrzanie o 1 stopień powoduje jednakowy wzrost objętości.
Współczynniki rozszerzalności gazów mają wartość:
1
K 1
273.15
t
V V0 1
273.15
273.15 t
V0
273.15
V = const – przemiana izochoryczna
3
m
pV
RT
M
p
const
T
ciśnienie
V1 < V2 < V3
p0T
p
T0
0
0
temperatura
J.A. Charles(1787 r.)
4
Q = 0 – przemiana adiabatyczna
pV const
cp
cv
Jak można zmienić stan układu?
Stan początkowy gazu -
p0 ,V0
Siła parcia gazu na tłok
p0 S
F
F
jest równoważona przez zewnętrzną siłę
2F
Zmniejszamy siłę zewnętrzną.
Gaz podnosi tłok
wykonuje
pracę.
Zdolność do wykonania pracy świadczy o
tym, że układ posiada pewien zasób energii
energia wewnętrzna układu
Energia wewnętrzna
Każdy makroskopowy układ fizyczny posiada pewien zasób energii
wewnętrznej.
Energia wewnętrzna jest funkcją stanu układu.
Każdej pracy wykonanej przez układ lub pracy wykonanej nad
układem przez siły zewnętrzne towarzyszy zmiana stanu układu –
zmiana energii wewnętrznej.
Energia wewnętrzna układu znajdującego się w kontakcie
termicznym z innym układem również ulega zmianie.
Zmiana energii
wewnętrznej układu
praca
wymiana ciepła
Różny od pracy sposób wymiany energii nazywa się wymianą
energii na sposób ciepła.
Energia wewnętrzna to:
• energia kinetyczna ruchu cieplnego cząsteczek
• energia kinetyczna związana z wewnętrznymi stopniami swobody
– rotacja, oscylacje, itp.
• energia potencjalna oddziaływania cząsteczek
• oraz wszelkie inne rodzaje energii.
Energia wewnętrzna – ekstensywna funkcja stanu.
Wyznaczamy zmianę energii wewnętrznej – podobnie jak energia
potencjalna.
I zasada termodynamiki
Przyrost energii wewnętrznej układu w dowolnym procesie
termodynamicznym jest równy sumie pracy wykonanej nad układem i
dostarczonego ciepła
dU W Q
Funkcja stanu,
jednoznacznie
określona
Zależą od rodzaju
procesu, nie są
ściśle określone
Doświadczenie Joule’a
James Prescott Joule
(1818-1898)
Z określonej ilości pracy
otrzymuje się zawsze taką
samą ilość ciepła.
• naczynie kalorymetryczne z wodą
(rtęcią),
• mieszadło – skonstruowane tak, by
opór przy mieszaniu był duży
• izolacja cieplna – układ
adiabatyczny,
• układ napędzający mieszadło,
• ciężar wykonujący pracę w polu
grawitacyjnym,
• termometr
Taki sam efekt można osiągnąć dostarczając do układu energię
na sposób ciepła
obydwa sposoby wymiany
energii są sobie równoważne.
Historycznie sformułowanie I zasady termodynamiki
Sumaryczna energia Wszechświata jest stała
nie można jej tworzyć lub niszczyć
a jedynie przekazywać między układami
(H. Helmholtz, 1821-1894)
dU W Q
Praca pobrana przez gaz – wykonana przez siły zewnętrzne
W 0
Ciepło pobrane przez gaz – zwiększające jego energię wewnętrzną
Q 0
Praca oddana na zewnątrz – wykonana przez gaz
W 0
Ciepło oddane przez gaz – zmniejszające jego energię wewnętrzną
Q 0
Wnioski z I zasady termodynamiki
układ termodynamiczny ma energię wewnętrzną, która jest funkcją
stanu układu
we wszystkich procesach przy zmianie energii wewnętrznej układu
obowiązuje zasada zachowania energii
przyrost energii wewnętrznej układu równa się sumie ilości pracy i
ciepła pobieranego przez układ z zewnątrz
praca i ciepło nie są funkcjami stanu – są funkcjami procesu
praca i ciepło to dwa rodzaje przekazu energii
po zakończeniu procesu nie ma ani pracy ani ciepła – przechodzą one w
energię wewnętrzną układu
jeżeli nastąpiła zmiana energii wewnętrznej układu podczas pewnego
procesu – to przy nieznajomości tego procesu nie potrafimy powiedzieć
ile energii pobrał układ w formie pracy a ile w formie ciepła
w procesie adiabatycznym
Q 0 dU W