Rozdział 12 MINI-UKŁAD PLANETARNY

Rozdział 12
MINI-UKŁAD PLANETARNY
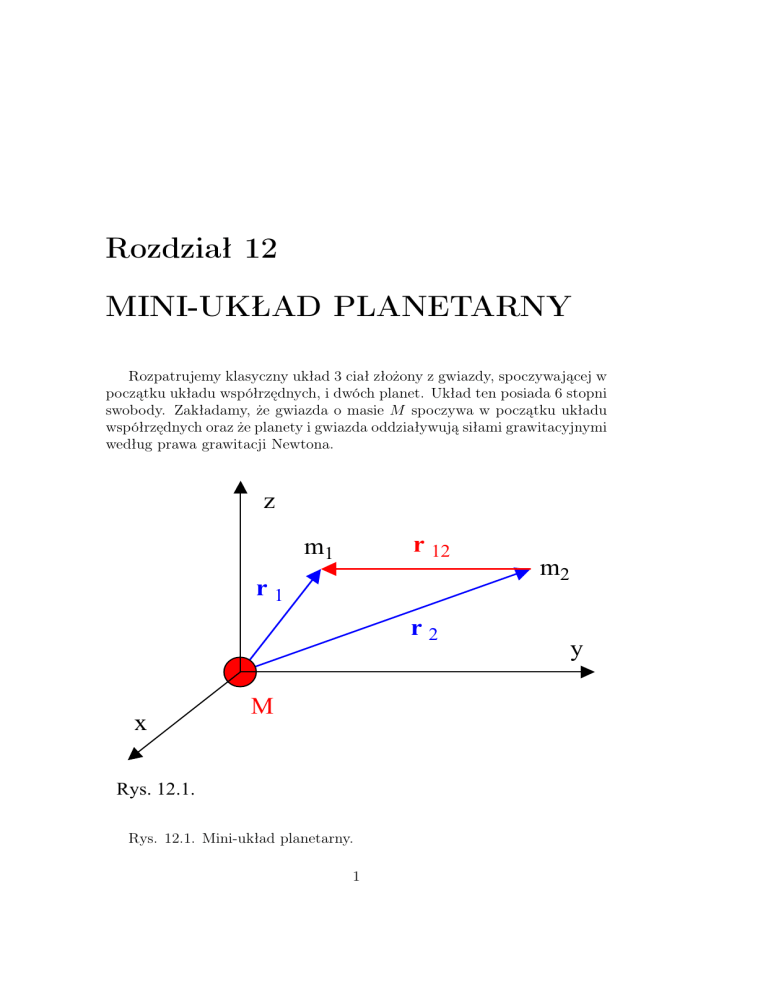
Rozpatrujemy klasyczny układ 3 ciał złożony z gwiazdy, spoczywającej w
początku układu współrzędnych, i dwóch planet. Układ ten posiada 6 stopni
swobody. Zakładamy, że gwiazda o masie M spoczywa w początku układu
współrzędnych oraz że planety i gwiazda oddziaływują siłami grawitacyjnymi
według prawa grawitacji Newtona.
]
P
U
U
U
[
0
5\V
Rys. 12.1. Mini-układ planetarny.
1
P
\
2
Rozdział 12. Mini-układ planetarny
Mini-układ planetarny opisany jest za pomocą równań ruchu
m1 a1 = F1 + F12 ,
(12.1)
m2 a2 = F2 + F21 ,
(12.2)
gdzie siła przyciągania j-tej planety przez gwiazdę
Fj = −GM
mj
rj
rj3
(j = 1, 2) ,
(12.3)
a siła przyciągania wzajemnego planet
F12 = −G
m1 m2
r12 .
3
r12
(12.4)
Zgodnie z 3. prawem dynamiki Newtona
F21 = −F12 .
(12.5)
Ze względu zachowawczy charakter sił grawitacyjnych energia całkowita
układu jest zachowana, czyli
0
Etot
= Etot = const
(12.6)
Warunek stabilności (wiązania) układu ma postać
0
Etot
= Etot = const < 0
(12.7)
i jest podyktowany przez warunki początkowe
r0j = rj (0),
v0j = vj (0) .
(12.8)
Janusz Adamowski
METODY OBLICZENIOWE FIZYKI
3
W celu uproszczenia zapisu równań oraz prezentacji graficznej podamy
szkic opisu mini-układu planetarnego w dwóch wymiarach, czyli dla f = 4.
Równania ruchu (12.1) i (12.2) mogą być całkowane numerycznie za pomocą
metody Eulera. Rozpisujemy równania (12.1) i (12.2) na płaszczyźnie x − y
GM
Gmj 0
0
xj − 3 (x1 − x2 )(−1)j
3
rj
r12
(12.9)
GM
Gmj 0
0
y
−
(y1 − y2 )(−1)j ,
j
3
3
rj
r12
(12.10)
axj = −
ayj = −
przy czym dla j = 1, 2 wskaźnik j 0 przyjmuje odpowiednio wartości j 0 = 2, 1.
Ponadto w równaniach (12.9) i (12.10)
rj =
q
x2j + yj2
q
r12 =
(x1 − x2 )2 + (y1 − y2 )2 .
4
Rozdział 12. Mini-układ planetarny
Algorytm rozwiązywania układu równań (12.9) i (12.10) metodą Eulera
na siatce czasowej zdefiniowanej w przedziale [t0 , tk ] jako tn+1 = tn + h, gdzie
h jest krokiem czasowym, a n = 0, 1, . . ..
(0) Zadajemy warunki początkowe dla t0 = 0
x0j = xj (0) ,
0
vxj
= vxj (0) ,
yj0 = yj (0) ,
(12.11)
0
vyj
= vyj (0) .
(12.12)
(i) Podstawiamy
xj = x0j ,
0
vxj = vxj
,
yj = yj0 ,
0
vyj = vyj
.
(ii) Obliczamy przyspieszenia wg wzorów (12.9) i (12.10).
(iii) Obliczamy położenia i prędkości dla tn+1 = tn + h stosując metodę
Eulera, czyli wykonujemy rachunki
xj (tn+1 ) = xj (tn ) + hvxj (tn )
(12.13)
yj (tn+1 ) = yj (tn ) + hvyj (tn )
(12.14)
vxj (tn+1 ) = vxj (tn ) + haxj (tn )
(12.15)
vyj (tn+1 ) = vyj (tn ) + hayj (tn )
(12.16)
(iv) Powtarzamy rachunki dla kolejnych tn zaczynając od punktu (ii).
Janusz Adamowski
METODY OBLICZENIOWE FIZYKI
5
Mini-układ planetarny może wykazywać trojaką niestabilność:
(1) ucieczka planet (planety) do nieskończoności, czyli brak wiązania,
(2) zderzenia planet z sobą,
(3) spadanie na centrum (zderzenie planety z gwiazdą), co wiąże się z niezachowaniem krętu pojedynczej planety.