podstawy astronomii

PODSTAWY ASTRONOMII
LISTA 6
1.
Na podstawie zdjęć Ziemi wykonanych przez sztucznego satelitę stwierdzono, że średnica kątowa tarczy Ziemi zmienia się w
czasie pełnego obiegu satelity od 1=132' do 2=1340'. Oblicz okres obiegu tego satelity, zakładając, że Ziemia jest kulą o
promieniu R=6371 km. Przyjmij, że satelita stacjonarny obiega Ziemię w odległości D= 42 200 km od jej środka.
2. Jeśli planeta ma okres synodyczny wynoszący 2.135 lat to, jaka jest półoś wielka jej orbity?
3. Kiedy podczas centralnego zaćmienia Księżyca faza całkowitego zaćmienia trwa dłużej:
 gdy Księżyc podczas całkowitego zaćmienia przechodzi przez perygeum czy
 gdy Księżyc podczas całkowitego zaćmienia przechodzi przez apogeum?
W rozważaniu przyjmij, że orbita Ziemi jest okręgiem. Odpowiednie dane liczbowe wyszukaj samodzielnie.
4. Przez ile dni w roku Ziemia znajduje się bliżej Słońca niż 1 AU?
5. Oblicz masę Neptuna w jednostkach masy Ziemi wiedząc, że jego satelita odległy od planety o 354 000 km ma okres obiegu 5
dni 21 godzin.
6. Jak zmieniłby się okres obiegu planety, gdyby jej masa stała się zaniedbywalnie mała względem Słońca?
7.
Policz, jak długo trwa podróż z Ziemi na Księżyc zakładając najniższe wymagania energetyczne takiego lotu.
8. Wyznacz moment pędu ciała znajdującego się na orbicie kołowej oraz orbicie eliptycznej o zadanym mimośrodzie. Od czego
zależy iloraz obu tych wielkości?
m
9. Gwiazda A ma jasność widomą mA=1 .5. Gwiazda B znajduje się 10 razy bliżej, a jej jasność absolutna jest 10 razy mniejsza. Jaka
jest jasność widoma gwiazdy B?
m
10. Paralaksa Proximy Centauri wynosi 0''.76 a jasność obserwowana 10 .5. Oblicz moduł odległości i jasność absolutną tej gwiazdy.
Ile razy Proximy Centauri jest słabsza od Słońca?
11. Jaką maksymalną jasność obserwowaną z Ziemi miałaby planeta o albedo 2 razy większym od albedo Ziemi, promieniu 2000 km
m
i krążąca po orbicie o promieniu 101 AU ? Jasność Ziemi w pełni w odległości 1 AU wynosi -3 .9.
m
12. Ile wynosi jasność absolutna Jowisza? W obliczeniach przyjmij mJ=-2 .2 dla opozycji tej planety. Porównaj otrzymany wynik z
m
jasnością absolutną Słońca (MS=4 .8). Czy przy obecnych środkach technicznych Jowisz mógłby być dostrzeżony z odległości 10 pc?
m
13. Gromada kulista, położona w odległości 2500 pc, składa się z 100 tys. gwiazd, z których 1000 ma jasność absolutną M 1=0 .0, a
m
reszta M2=5 .0. Jaka jest całkowita jasność obserwowana tej gromady?
m
14. Jasność absolutna galaktyki M32 wynosi -15 .7. Oszacuj, z ilu gwiazd składa się ta galaktyka zakładając, że w jej skład wchodzą
m
tylko gwiazdy podobne do Słońca oraz, że widzimy tylko ich połowę. Jasność obserwowana Słońca wynosi mS=-26 .7.
15. Policz temperaturę efektywną Słońca i strumień promieniowania wychodzący z jego powierzchni wiedząc, że w odległości 1 AU
2
średnica kątowa Słońca wynosi θS=32', a mierzony strumień promieniowania fS=1360 W/m . Jak inaczej nazywa się ta druga
wielkość i czy jest stała w czasie?
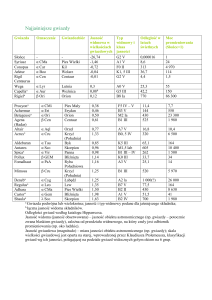
16. Obliczyć promień (w R) gwiazd: Agena, Antares i Syriusz B znając ich temperatury efektywne i jasności absolutne bolometryczne.
Gwiazda
Agena ( Cen)
Antares ( Sco)
Syriusz B ( CMa B)
Słońce
Teff [K]
21000
3100
7500
5770
m
Mbol [ ]
-3.8
-4.6
11.6
4.75
17. Obliczyć promień białego karła, którego widoma jasność wynosi mV=8m.5 i paralaksa =0''.2. Poprawka bolometryczna wynosi BC=-2m.1, a
Teff=28000 K.
18. Wyznaczyć absolutną jasność bolometryczną gwiazdy w funkcji jej temperatury i promienia (dane dla Słońca w tabeli powyżej, R=1).
19. Gwiazda potrójna składa się z trzech składników: A, B i C. Składnik A jest 3 razy jaśniejszy niż B, a składnik B jest 4 razy jaśniejszy niż C. Widoma
A
m
jasność bolometryczna składnika A wynosi m bol=3 .45. Jakie są mbol składników B i C oraz układu jako całości? Temperatury efektywne
A
B
C
składników wynoszą: T eff=3000 K, T eff=4500 K i T eff=6000 K. Policzyć promienie składników A i B (w R) wiedząc, że promień składnika C jest
równy promieniowi Słońca. Wyznaczyć odległość tego układu od Słońca.
20. Wykaż, że zmiana temperatury efektywnej T gwiazdy o małą wartość T oraz zmiana promienia R tej gwiazdy o małą wartość R spowoduje
zmianę widomej jasności bolometrycznej gwiazdy o wartość gdzie s jest wielkością bardzo małą wobec pozostałych składników.
T
R


m  2.5 lg1  4
2
 s 
T
R

