Magnetostatyka. Cewki indukcyjne

91
Elektrotechnika podstawowa
ROZDZIAŁ 5
Magnetostatyka. Cewki indukcyjne
Pole magnetyczne powstaje w wyniku przemieszczeń (zmian) ładunków elektrycznych. Mówi się
więc o wytwarzaniu tego pola przez źródłowe elementy prądowe.
Najczęściej rozważa się przypadki pól magnetycznych występujących wokół przewodów z prądem.
Między położonymi blisko siebie przewodami z prądem występują siły (oddziaływanie elektrodynamiczne).
Stosując materiały o szczególnych własnościach magnetycznych (ferromagnetyki) uzyskuje się
koncentrację strumieni magnetycznych wzdłuż określonych dróg, tworzących obwód magnetyczny.
Analiza obwodów magnetycznych jest utrudniona z powodu nieliniowości charakterystyk magnesowania ferromagnetyków.
Fundamentalne znaczenie odgrywa w elektrotechnice: prawo indukcji elektromagnetycznej. Wskutek zmiany strumienia skojarzonego z cewką, indukuje się w niej napięcie. Jeśli strumień skojarzony z cewką pochodzi od prądu tejże cewki, to występuje zjawisko samoindukcji, a jeśli od prądu
innej cewki – zjawisko indukcji wzajemnej.
Dzięki indukcji wzajemnej możliwe jest przenoszenie energii z jednego obwodu elektrycznego do
drugiego obwodu elektrycznego na drodze magnetycznej. Taki proces zachodzi w transformatorze.
Posługując się wielkością zwaną przekładnią transformatora, sprowadza się jego schemat dwuobwodowy do schematu jednoobwodowego.
92
Elektrotechnika podstawowa
Oznaczenia wielkości występujących w rozdziale 5
a
B
Br
Bs
eind
Fµ
∆F
F
∆F
Hc
H
i
iL
I
k
l
∆l
∆l
L
Lg
Ls
Lµ
M
M
∆M
∆M
pµ
∆Q
odległość od przewodu z prądem
indukcja magnetyczna
remanencja (indukcja szczątkowa, pozostałość magnetyczna)
indukcja nasycenia
siła elektromotoryczna (sem) indukowana
siła magnetomotoryczna
wartość bezwzględna siły działającej
na element prądowy
siła
siła działająca na element prądowy
koercja (natężenie koercji, natężenie
powściągające)
natężenie pola magnetycznego
prąd
hipotetyczny prąd Lenza
prąd stały
współczynnik sprzężenia magnetycznego
długość przewodu; długość drogi strumienia
długość elementu prądowego
wektor długości elementu prądowego
indukcyjność własna
indukcyjność główna
indukcyjność rozproszenia
indukcyjność główna (magnesująca)
transformatora
indukcyjność wzajemna
polaryzacja magnetyczna (magnetyzacja)
wartość bezwzględna momentu działającego na dipol magnetyczny
moment działający na dipol magnetyczny
dipolowy moment magnetyczny
ładunek elementu prądowego
Literatura do rozdziału 5
[1], [2], [3], [4], [5], [6], [8]
r
r
RFe
Rµ.k
S
∆S
∆S
t
u
uind
Uµ
∆v
v
Wµ
z
ϑ
κ
Θ
Λµ.k
µ
µr
µ0
ρWµ
Φ
∆Φ
Ψ
odległość
wektor odległości; promień
rezystancja poprzeczna schematu transformatora
reluktancja (opór magnetyczny)
pole powierzchni; pole przekroju rdzenia (magnetowodu)
pole elementu powierzchni; pole płaskiej pętli prądu
wektor normalny do elementu powierzchni ∆S
czas
napięcie
napięcie indukowane
napięcie magnetyczne
objętość przestrzeni elementarnej
prędkość; prędkość ładunku elementu
prądowego
energia pola magnetycznego
liczba zwojów uzwojenia (cewki)
przekładnia transformatora
podatność magnetyczna
przepływ prądu
permeancja (przewodność magnetyczna)
przenikalność magnetyczna
przenikalność magnetyczna względna
stała magnetyczna (przenikalność magnetyczna próżni)
przestrzenna (objętościowa) gęstość
energii pola magnetycznego
strumień magnetyczny; strumień magnetyczny przenikający przez powierzchnię S
strumień magnetyczny przenikający
przez powierzchnię ∆S
strumień skojarzony
93
5. Magnetostatyka. Cewki indukcyjne
Wykład XI. POLE I OBWODY MAGNETYCZNE
Pole magnetyczne i jego źródła
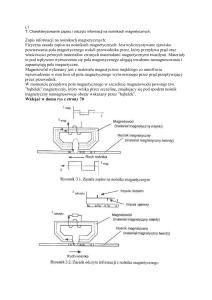
a)
Występowanie oddziaływań magnetycznych (pól magnetycznych)
v
∆Q
wiąże się z prądem elektrycznym. Źródłami pola magnetycznego są
I
tzw. elementy prądowe, mianowicie: ładunki poruszające się z okreb)
śloną prędkością (rys. a); odcinki przewodów z prądem elektrycznym
∆l
(rys. b); płaskie pętle, tj. zamknięte obwody, zwoje, ramki, w których
c)
płynie prąd elektryczny (rys. c).
I
N
Małą, płaską pętlę prądu nazywamy dipolem magnetycznym. Można go
S
∆S
traktować jako układ elementarny dwóch biegunów magnetycznych.
Każdy z występujących w przestrzeni elementów prądowych przyczynia się do powstania wypadkowego pola magnetycznego, a gdy sam znajduje się w polu magnetycznym pochodzącym od innych elementów prądowych, podlega określonemu działaniu tego pola. Na pole magnesu trwałego
składają się w głównej mierze pola związane ze spinowymi ruchami elektronów.
Indukcja magnetyczna
Podstawową wielkością charakteryzującą pole magnetyczne jest indukcja magnetyczna B. Definiując tę wielkość korzysta się z zależności określających siłę lub moment, z jaką pole magnetyczne
działa na próbne elementy prądowe. Podobnie – za pomocą siły działającej w polu elektrycznym na
próbny ładunek – zostało określone natężenie pola elektrycznego (rozdz. 1).
α
B
a) ∆Q⋅ v
Próbny element prądowy określonego rodzaju wyraża się ilościowo
v
jako:
∆Q
- iloczyn małego ładunku elektrycznego ∆Q i wektora jego
∆F
prędkości v (rys. a),
α
b) I⋅ ∆l
B
- iloczyn prądu I płynącego w krótkim, prostoliniowym odcinku
∆l
przewodu, i wektora jego długości ∆l o zwrocie zgodnym ze zwroI ∆F
tem prądu (rys. b),
- iloczyn prądu I i wektora pola powierzchni ∆S płaskiej pętli
c) I⋅ ∆S
B
α
prądu, nazywany dipolowym momentem magnetycznym; przy czym
I
moduł ∆S równa się polu powierzchni ∆S, kierunek ∆S jest zgod∆S
pµ
ny z normalną do powierzchni, a zwrot – ustalony względem zwro∆M
tu prądu zgodnie z regułą korkociągu (rys. c).
Siła ∆F (moduł ∆F)lub moment ∆M (moduł ∆M), działające na próbne elementy prądowe, to iloczyny wektorowe wyrażających je wielkości przez indukcję magnetyczną B:
- siła ∆F (N), nazywana siłą Lorentza, z jaką pole magnetyczne działa na ładunek elektryczny
∆Q (C), poruszający się z prędkością v (m s-1)
∆F = ∆Q ⋅ v × B ,
∆F = ∆Q ⋅ v ⋅ B ⋅ sin α ,
(5.1a, a’)
- siła ∆F (N), nazywaną siłą Ampere’a, z jaką pole magnetyczne działa na mały, prostoliniowy
odcinek przewodu z prądem I (A), o długości skierowanej ∆l (m)
∆F = I ⋅ ∆l × B ,
∆F = I ⋅ ∆l ⋅ B ⋅ sin α ,
(5.1b, b’)
- moment ∆M (N m), z jaką pole magnetyczne działa na dipol magnetyczny o prądzie I (A) i
powierzchni ∆S (m2)
∆M = I ⋅ ∆S × B = p µ × B ,
∆M = I ⋅ ∆S ⋅ B ⋅ sin α ,
(5.1c, c’)
przy czym dipolowy moment magnetyczny
p µ = I ⋅ ∆S .
(5.1c”)
Jak widać, między miarami elementów prądowych i modułami sił lub momentów, działających na
te elementy w polu magnetycznym, zachodzi proporcjonalność wyrażona współczynnikiem
( B ⋅ sin α ) . Moduły sił ∆F i momentów ∆M osiągają największe wartości, jeśli wielkości występu-
94
Wykład XI
jące w iloczynach wektorowych zależności: (5.1a), (5.1b) oraz (5.1c), są do siebie prostopadłe
(α = π/2). Zakładając prostopadłość wektorów odpowiednich wielkości (odpowiednie ustawienie
elementu prądowego w polu magnetycznym), definicję indukcji B można uformować – wg zależności: (5.1a’), (5.1b’) oraz (5.1c’) – na podstawie granicznych wartości modułów:
∆Fmax
∆Fmax
∆M max
,
,
.
(5.2a, b, c)
B = lim
B = lim
B = lim
∆Q →0 ∆Q ⋅ v
∆l →0 ∆l ⋅ I
∆S →0 ∆S ⋅ I
Jednostką indukcji magnetycznej jest tesla (T), wyrażana w jednostkach innych wielkości jako weber na metr do kwadratu (Wb⋅m-2) albo wolt razy sekunda na metr do kwadratu (V⋅s⋅m-2).
Jeśli moduł, kierunek i zwrot siły lub momentu pochodzenia magnetycznego, jakie działają na określony element prądowy, są stałe w dowolnym miejscu rozważanej przestrzeni (przy jednakowym
zorientowaniu elementu względem osi układu współrzędnych), to indukcja magnetyczna jest stała
co do modułu, kierunku i zwrotu. Pole magnetyczne występujące w tej przestrzeni jest polem równomiernym.
Krzywe styczne we wszystkich punktach do wektora indukcji magnetycznej, zgodnie z nim skierowane, noszą nazwę linii pola magnetycznego. Efekt działania pola na elementy prądowe jest najsilniejszy, jeśli są one skierowane pod kątem prostym do linii pola magnetycznego.
Na ładunek elektryczny poruszający się w polu magnetycznym działa siła skierowana prostopadle
do płaszczyżny wyznaczonej przez linie pola i wektor prędkości ładunku. Tor ruchu cząstki w stałym, równomiernym polu magnetycznym ulega więc zakrzywieniu. Przykładem takiego działania
jest odchylanie wiązki elektronów w lampie kineskopowej.
Na odcinek przewodu prostoliniowego z prądem działa siła wypychająca go w kierunku prostopadłym do płaszczyzny wyznaczonej przez linie pola i przewód.
Na płaski zwój przewodu z prądem działa moment obracający go prostopadle do płaszczyzny wyznaczonej przez linie pola i normalną do płaszczyzny zwoju.
Strumień magnetyczny
Strumień magnetyczny ∆Φ przenikający przez powierzchnię ∆S , tzn. strumień wektora indukcji
magnetycznej B przez element powierzchni ∆S (rys.), jest skalarem
∆Φ = B ⋅ ∆S = B ⋅ ∆S ⋅ cos α .
(5.3a)
gdzie ∆S = ∆S⋅1n – wektor normalny do elementu powierzchS
∆S
ni ∆S (w przypadku powierzchni zamkniętej – skierowany
∆Φ
na
zewnątrz tej powierzchni).
Φ
Strumień magnetyczny Φ przenikający przez powierzchnię S,
tzn.
całka powierzchniowa B po S , jest skalarem
S
∆S
Φ = ∫ B ⋅ dS .
(5.3b)
α
B
S
W równomiernym polu magnetycznym strumień Φ przez powierzchnię S prostopadłą do B (moduł: B) jest równy iloczynowi
Φ = B⋅S .
(5.3c)
Jednostką strumienia magnetycznego jest weber (Wb) czyli wolt razy sekunda (V⋅s).
Strumień magnetyczny przenikający przez powierzchnię zamkniętą jest zawsze równy zeru
(5.4)
∫ B ⋅ dS = 0 .
1
∆S
S
Wynika z tego, że pole magnetyczne jest polem bezźródłowym (solenoidalnym), a jego linie są liniami zamkniętymi. Stwierdzenie to wyraża tzw. zasadę ciągłości linii pola magnetycznego.
W przestrzeni ograniczonej liniami pola magnetycznego strumień ma stałą wartość. Można więc
tworzyć „rurki” („komórki”) strumienia magnetycznego, z nich zaś – obwód magnetyczny, przypominający obwód elektryczny. Rola strumienia magnetycznego w analizie obwodów magnetycznych
jest podobna do roli prądu elektrycznego w analizie obwodów elektrycznych.
95
5. Magnetostatyka. Cewki indukcyjne
Natężenie pola magnetycznego. Przenikalność magnetyczna
Wektor indukcji magnetycznej B pola wytworzonego przez określony układ elementów prądowych
zależy od własności magnetycznych środowiska.
Wielkością magnetyczną, która nie zależy od własności środowiska, a tylko od rodzaju i układu
geometrycznego elementów prądowych wytwarzających pole, jest natężenie pola magnetycznego H.
W środowisku izotropowym wektory B i H mają ten sam kierunek i zwrot, a związek ten wyraża
się zależnością (wektorowo i skalarnie):
B = µ⋅H ,
B = µ⋅H .
(5.5a, b)
Występująca w nim wielkość µ to przenikalność magnetyczna, będąca iloczynem stałej magnetycznej
(przenikalności magnetycznej próżni) µ0 i przenikalności magnetycznej względnej środowiska µr:
µ = µ0 ⋅ µr .
(5.5c)
Przenikalność magnetyczna µ jest podstawową stałą materiałową magnetyka.
Jednostką natężenia pola magnetycznego jest amper na metr (A⋅m-1). Odwołując się do jednostki
indukcyjności – henra (H) czyli omosekundy (Ω⋅s), stałą magnetyczną µ0 i przenikalność magnetyczną µ wyraża się w henrach na metr (H⋅m-1) czyli omach razy sekunda na metr (Ω⋅s⋅m-1).
Stała magnetyczna ma wartość µ0 = 4π ⋅ 10 – 7 H/m.
Prawo Biota-Savarta-Laplace’a. Prawo przepływu prądu (prawo Ampere’a)
W środowisku jednorodnym i izotropowym obowiązuje zasada superpozycji pól magnetycznych
pochodzących od różnych źródeł. Natężenie pola pochodzące od przewodu z prądem jest równe
sumie natężeń pochodzących od odcinków tego przewodu. Wkład (przyczynek) dH – elementarnego odcinka przewodu dl z prądem i – do natężenia pola magnetycznego H w punkcie położonym w
odległości r od dl (rys. a), zapisuje się w postaci wektorowej albo skalarnej:
i
i ⋅ dl
a)
(5.6a)
dH =
⋅
(
d
l
×
r
)
=
⋅ (1dl × 1r ) ,
3
2
4
π
⋅
r
4
π
⋅
r
dl
α
i
dH
i ⋅ dl
(5.6b)
dH =
⋅ sin α .
r
4π ⋅ r 2
Powyższa formuła słowna oraz zależności analityczne (5.6a) i
b)
H
(5.6b) wyrażają prawo Biota-Savarta-Laplace’a.
ik
dl
Całka liniowa wektora natężenia pola magnetycznego H po
krzywej zamkniętej (całka okrężna) równa się sumie prądów
przenikających (przepływowi prądu Θ ) przez powierzchnię rozpiętą na tej krzywej (rys. b):
k = 1, 2, ...
c)
n
∫ H ⋅ dl = ∑ ik = Θ .
B, H
I
B, H
I
L
(5.7)
k =1
Powyższa formuła słowna oraz zależność analityczna (5.7) wyrażają prawo przepływu prądu (prawa Ampere’a).
Wartość całki we wzorze (5.7) jest w ogólnym przypadku różna
od zera. Pole magnetyczne jest więc polem wirowym.
Linie pola magnetycznego wokół nieskończenie długiego przewodnika z prądem układają się koncentrycznie (rys. c).
Przykład. Na podstawie praw Biota-Savarta-Laplace’a oraz Ampere’a, zostanie wyprowadzony
wzór na natężenie pola magnetycznego H w odległości a od nieskończenie długiego przewodu z
prądem i.
96
Wykład XI
I sposób. Z rys. c’ wynikają zależności:
x = a ⋅ ctg(π − α ) = − a ⋅ ctg α ,
zatem
a
dx =
⋅ dα ,
sin 2 α
c’)
a
,
sin α
a2
r2 =
,
sin 2 α
r=
a
r
π
H =∫
i
4π ⋅ a
0
⋅ sin α ⋅ dα =
1r
π -α
i
i
2π ⋅ a
II sposób. Z rys. c” i wzoru (5.7) wynika równanie
i
2π ⋅ a ⋅ H = i , stąd H =
.
2π ⋅ a
.
α
x
x dx 1x
0
a po podstawieniu tych wyrażeń do wzoru (5.6b)
otrzymuje się
y
dH, H
c”)
H
i
a
Oddziaływanie elektrodynamiczne. Definicja jednostki prądu elektrycznego
Położone blisko siebie przewody z prądem przyciągają się lub odpychają. Oddziaływania tego rodzaju zwykło się określać jako elektrodynamiczne.
W przypadku dwóch prostoliniowych, nieskończenie długich, biegnących równolegle do siebie, cienkich przewodów z prądem (rys. poniżej oraz wzór otrzymany w przedstawionym wyżej przykładzie):
- siła Ampere’a działająca na jednostkę długości pierwszego prze∆F1
i1
wodu, pochodząca od prądu drugiego przewodu
B2 ∆l1
F1
i
µ
a
= i1 ⋅ B2 = i1 ⋅ µ ⋅ 2 =
⋅ i1 ⋅ i2 ,
(5.8a)
i2
B1 ∆l2
l
2π ⋅ a 2π ⋅ a
- siła Ampere’a działająca na jednostkę długości drugiego prze∆F2
wodu, pochodząca od prądu pierwszego przewodu
∆l 1 i 1
F2
i
µ
= i2 ⋅ B1 = i2 ⋅ µ ⋅ 1 =
⋅ i1 ⋅ i2 ,
(5.8b)
B2
∆F1
l
⋅
a
⋅
a
2
π
2
π
a
∆F2 i2
B1
F1 F2
µ
więc
=
=
⋅ i1 ⋅ i2 .
(5.8c)
∆l 2
l
l
2π ⋅ a
Widać, że przewody odpychają się przy przeciwnym zwrocie prądów, a przyciągają – przy zgodnym.
F
Jeśli: i1 = i2 = 1 A, µ = µ 0 = 4π ⋅ 10 −7 H/m, a = 1 m, to
= 2 ⋅ 10 −7 N/m.
l
W ten sposób, za pomocą siły oddziaływania elektrodynamicznego przewodów z prądem elektrycznym, definiuje się podstawową jednostkę elektryczną: amper (A) jest natężeniem prądu, który
płynąc w dwóch prostoliniowych, nieskończenie długich przewodach o pomijalnie małym
przekroju kołowym, umieszczonych w próżni i biegnących równolegle do siebie w odległości 1 m,
wywołuje między nimi siłę równą 2⋅10-7 N na każdy metr długości.
Diamagnetyki i paramagnetyki
O magnetycznych właściwościach ciał decyduje budowa atomów i ich przestrzenne, wzajemne ułożenie. Wspomniane wcześniej prądy molekularne, odpowiadające orbitalnym i spinowym ruchom
elektronów oraz przypisanym im orbitalnym i spinowym momentom magnetycznym, są głównym
źródłem wypadkowych pól magnetycznych atomów. Ruchom protonów i neutronów wewnątrz jąder atomów odpowiadają wypadkowe momenty magnetyczne jąder, ale są one około 2000 razy
mniejsze od orbitalnego i spinowego momentu elektronu.
Jeśli atomy ciała nie wytwarzają wypadkowego pola magnetycznego w nieobecności zewnętrznego
pola magnetycznego, czyli pola orbitalne oraz spinowe atomów kompensują się, to ciało takie zalicza się do diamagnetyków.
5. Magnetostatyka. Cewki indukcyjne
97
pµ 1
Pod wpływem zewnętrznego pola magnetycznego występują w
B=0
nich niewielkie zmiany wypadkowych momentów magnetyczpµ 1 =  pµ 2 
pµ 2
pµ = pµ 1 + pµ 2 = 0
nych par elektronów, które zajmują w atomach te same poziomy
energetyczne (rys. obok). Reakcja każdej pary elektronów na
zewnętrzne pole magnetyczne jest podobna. Powstaje słabe,
B≠0
pµ 1’
wypadkowe wewnętrzne pole magnetyczne, skierowane przeB
p
’
<

p
’

µ
1
µ
2
ciwnie do pola zewnętrznego. Efekt ten, wyrażający się osłabiepµ ’ = pµ 1’+ pµ 2’≠ 0
pµ 2’
niem w nikłym stopniu pola zewnętrznego, określa się jako efekt
diamagnetyczny.
Jeśli atomy ciała wytwarzają wypadkowe pole magnetyczne, czyli pola orbitalne oraz spinowe atomów nie kompensują się, a kierunki i zwroty pól w ramach tworzonych przez cząsteczki struktur
przestrzennych są zupełnie dowolne, to ciało takie zalicza się do paramagnetyków.
Atomy paramagnetyków można przedstawić jako elementarne
magnesy, które dążą do zajęcia położenia zgodnego z polem
B=0
×
zewnętrznym (rys. obok). Działanie to, utrudniane w znacznym
stopniu przez ruchy cieplne cząsteczek, prowadzi do powstania
wypadkowego wewnętrznego pola magnetycznego, skierowanego zgodnie z polem zewnętrznym. Wynikiem jest niewielkie
B≠0
×
wzmocnienie pola zewnętrznego, określane jako efekt paramagnetyczny. W paramagnetykach występuje również efekt diamagnetyczny, ale jest on słabszy od paramagnetycznego.
Zewnętrzne pole magnetyczne nie wpływa zatem wyraźnie na zmianę ustawienia dipoli magnetycznych w dia- i paramagnetykach. Ciała te nie mają szczególnych własności magnetycznych.
Przenikalność magnetyczna względna diamagnetyków jest znikomo mniejsza, a paramagnetyków –
znikomo większa od 1 (np. srebro ma µr ≅ 0,99998, zaś aluminium 1,00002). Diamagnetyki są
przez magnes słabo odpychane, a paramagnetyki słabo przyciągane.
Ferromagnetyki
Nadzwyczajne właściwości magnetyczne wykazują ferromagnetyki. Ich kryształy dzielą się na elementarne przestrzenne obszary samorzutnego namagnesowania, w których atomowe pola magnetyczne (typu paramagnetycznego) są zorientowane zgodnie, chociaż w różny sposób w poszczególnych obszarach. Obszary te nazwano domenami magnetycznymi. Domeny wyraźnie reagują na pojawienie się zewnętrznego pola magnetycznego. Dążą do zorientowania swych pól zgodnie z polem
zewnętrznym (dotyczy to głównie momentów spinowych elektronów) przez przejmowanie i podporządkowanie tej orientacji części cząsteczek sąsiednich domen i przez „poprawę” własnego ustawienia. Nazywa się to poglądowo obrotem i rozrostem domen, chociaż jedno i drugie zjawisko polega w zasadzie na tym samym: zmianie orientacji momentu dipoli magnetycznych. Efektem tego
„przeorientowania” jest magnesowanie się ciała. Ferromagnetyk nienamagnesowany jest silnie
przyciągany przez magnes, bowiem w wyniku przeorientowania domen sam staje się magnesem.
Po usunięciu zewnętrznego pola pozostaje w ferromagnetyku
wierzchołek
jakieś namagnesowanie. Zależnie od tego, jak jest ono duże,
pętli
histerezy
B
mówi się o materiale, że jest magnetycznie miękki albo magneBs
krzywa
tycznie twardy. Materiałów magnetycznie twardych używa się
magnesoBr
do wyrobu magnesów trwałych.
wania
Hc
H
Zależność B = f(H) materiałów ferromagnetycznych przedstawia
0
krzywe magnesowania pierwotnego i pętle histerezy (rys. obok).
pętla histerezy
Przenikalność magnetyczna względna µr różnych ferromagnetyBs – indukcja
ków – statyczna bądź dynamiczna poniżej punktu nasycenia –
nasycenia
zawiera się w przedziale wartości od kilkuset (nikiel – ok. 600)
Br – remanencja
Hc – koercja
do kilkuset tysięcy (czyste żelazo – ok. 200 tysięcy).
98
Wykład XI
Polaryzacja magnetyczna (magnetyzacja)
Zjawisko powstawania wewnętrznego pola magnetycznego pod wpływem pola zewnętrznego nazywa się
polaryzacją magnetyczną lub magnetyzacją – przez analogię do polaryzacji elektrycznej w dielektrykach.
Na zasadzie podobnej analogii wprowadza się pojęcie wektora polaryzacji magnetycznej, krótko: polaryzacji magnetycznej lub magnetyzacji M (oznaczenie rezerwowe J), określonego wzorami:
p µ .∆v
.
(5.9)
M = lim
∆v →0 ∆v
M =κ ⋅H ,
(5.10)
gdzie: ∆v – objętość,
pµ.∆v - suma momentów dipoli magnetycznych cząsteczek zawartych w objętości ∆v,
κ - podatność magnetyczna środowiska, wielkość bezwymiarowa.
Wypadkowe wewnętrzne pole magnetyczne może być skierowane – względem pola zewnętrznego
– zgodnie (paramagnetyki i ferromagnetyki) lub przeciwnie (diamagnetyki), zatem κ może przybierać wartości dodatnie i ujemne.
Indukcja magnetyczna wyraża się wzorem
B = µ 0 ⋅ µ r ⋅ H = µ 0 ⋅ H + µ 0 ⋅ M = µ 0 ⋅ (1 + κ ) ⋅ H ,
(5.11a)
µr = 1+ κ .
czyli
(5.11b)
Prawa dotyczące obwodów strumienia stałego (magnetostatycznych)
Pole magnetyczne związane z prądem stałym jest nazywane polem magnetostatycznym (magnetycznym statycznym). Polem magnetostatycznym jest także pole magnetyczne wytworzone przez magnes trwały. Zazwyczaj rozważa się przypadki pola magnetostatycznego w rdzeniu ferromagnetycznym (magnetowodzie) i występujących w nim szczelinach powietrznych. Stosowanie ferromagnetyka pozwala uzyskać koncentrację strumieni magnetycznych wzdłuż założonych dróg, które
tworzą obwód magnetyczny (pojęcie to odnosi się do układów ze strumieniami stałymi w czasie i
wolnozmiennymi).
Obwód magnetyczny jest to zespół elementów tworzących drogi zamknięte dla strumieni magnetycznych, wraz ze źródłami tych strumieni, którymi są prądy elektryczne w uzwojeniach lub magnesy trwałe. Z powodu stosowania ferromagnetyków, obwody magnetyczne są z reguły nieliniowe.
Gałęziami obwodu magnetycznego są odcinki o stałym strumieniu, zaś węzłami – miejsca rozgałęziania się strumieni gałęziowych. Gałęzie składają się na ogół z odcinków o stałym przekroju.
Przyjmuje się, że pole magnetyczne jest w tych przekrojach równomierne.
Suma strumieni magnetycznych w węzłach jest równa zeru (I prawo Kirchhoffa dla obwodu magnetycznego), co zapisuje się następująco:
(5.12)
∑Φ k = 0 ,
k
przy czym strumienie dopływające k-tych gałęzi bierze się tradycyjnie ze znakiem „plus”, a odpływające – ze znakiem „minus”.
Zgodnie z prawem Ampere’a, wzdłuż oczek obwodu magnetycznego – z uzwojeniami jako źródłami pola – obowiązują następujące, równoważne zależności (II prawo Kirchhoffa dla obwodu magnetycznego):
∑ H k ⋅ l k = ∑ I k ⋅ z k , ∑U µ .k = ∑Θ k , ∑U µ .k = ∑ Fµ .k , (5.13a, b, c)
k
k
przy czym:
k
U µ .k = H k ⋅ l k ,
k
k
Θ k = Fµ .k = I k ⋅ z k ,
k
(5.13d, e)
gdzie: Hk – natężenie pola magnetycznego w magnetyku k-tej gałęzi należącej do oczka,
lk – długość drogi strumienia w magnetyku k-tej gałęzi należącej do oczka,
Ik – prąd elektryczny w uzwojeniu k-tej gałęzi należącej do oczka,
zk – liczba zwojów uzwojenia k-tej gałęzi należącej do oczka,
99
5. Magnetostatyka. Cewki indukcyjne
Uµ.k – napięcie magnetyczne (mierzone w amperach) k-tej gałęzi należącej do oczka,
Θk – przepływ prądu, inaczej wzbudność (w amperach) k-tej gałęzi należącej do oczka,
Fµ.k – siła magnetomotoryczna (inaczej nazwany i oznaczony przepływ prądu) k-tej gałęzi
należącej do oczka.
Dla k-tych liniowych części (gałęzi) obwodu magnetycznego, np. szczelin powietrznych, wprowadza
się pojęcia reluktancji (oporu magnetycznego) Rµ.k i permeancji (przewodności magnetycznej) Λµ.k :
lk
µ ⋅S
1
R µ .k =
= k k ,
,
(5.14a, b)
Λ µ .k =
µk ⋅ Sk
R µ .k
lk
gdzie: lk – długość rozważanej, liniowej k-tej gałęzi obwodu magnetycznego,
Sk – powierzchnia przekroju poprzecznego, przez którą przenika strumień k-tej gałęzi,
µk – przenikalność magnetyczna materiału k-tej gałęzi.
Jednostką permeancji jest henr (H) czyli omosekunda (Ω⋅s).
Jednostką reluktancji jest odwrotność henra (H-1) czyli simens na sekundę (S⋅s-1).
a)
lk
B
Φ
Φ k Rµ .k
Skoro H = =
, więc U µ .k = H k ⋅ l k =
⋅ Φ k = R µ .k ⋅ Φ k
µ µ⋅S
µk ⋅ Sk
Uµ .k
(rys. a), zatem liniowej części obwodu magnetycznego odpowiadają nastęące zależności (prawo Ohma dla obwodu magnetycznego – rys. b):
puj
b)
Φ Rµ
U µ = Rµ ⋅ Φ ,
Φ = Λµ ⋅ U µ ,
(5.15a, b)
Uµ
c)
Φ
zaś nierozgałęzionemu liniowemu obwodowi magnetycznemu można przypisać równania (rys. c):
Θ = Rµ ⋅ Φ ,
Φ = Λµ ⋅ Θ ,
(5.16a, b)
Rµ
gdzie: Θ – przepływ całkowity, tzn. sumaryczny przepływ prądów uzwojeń;
Rµ i Λµ – reluktancja i permeancja części albo całego obwodu liniowego.
Θ
Obwód magnetostatyczny nierozgałęziony
Uzwojeniu nawiniętemu na rdzeń ze szczeliną powietrzną (rys. a) odpowiada nierozgałęziony obwód
magnetyczny, złożony z dwóch części (rys. b): nieliniowej pasywnej (żelazo) i liniowej aktywnej
(uzwojenie i szczelina powietrzna). Aby wyznaczyć Φ, znając Θ i wykres zależności nieliniowej
Bż (Hż), można skorzystać z metody przecięcia charakterystyk, znanej z teorii obwodów elektrycznych. W układzie współrzędnych Uµ ,Φ wrysowuje się charakterystyki części nieliniowej Φ ż (Uµ .ż )
i liniowej Φ p (Uµ .ż ), a następnie określa parametry odpowiadające punktowi ich przecięcia (rys. c).
Charakterystykę części nieliniowej pasywnej Φ ż (Uµ .ż ) uzyskuje się z przeskalowania charakterystyki magnesowania żelaza B(H), wg wzorów: U µ . ż = H ⋅ l ż , Φ ż = B ⋅ S ż .
Charakterystyka części liniowej aktywnej Φ p (Uµ .ż ) wynika z równania obwodu:
Θ = U µ . p + U µ . ż , czyli Θ = Rµ . p ⋅ Φ p + U µ . ż , zapisanego jako równanie prostej
Φ p = Φ p (U µ . ż ) =
Θ − U µ .ż
, gdzie stałymi są Θ = z ⋅ i i Rµ . p =
Rµ . p
B, H
a)
i
Φ
b)
Φp =Φ
Sp
.
Φż =Φ
Φp,Φż
Θ
Rµ .p
lp
z
µ0 ⋅ S p
c)
Sż
lż
lp
Θ
Uµ .p
Φ ż (Uµ .ż)
Rµ .p
Uµ .ż
(Rµ .ż)
Φ
Φ p (Uµ .ż)
Uµ .ż
0
Uµ .ż
Θ
100
Wykład XI
Zwykle nie przeskalowuje się danej wykreślnie charakterystyki magnesowania żelaza Bż (Hż) , tylko
pozostaje przy współrzędnych Hż , Bż , dostosowując do nich charakterystykę części liniowej:
B p ' (H ż ) =
Φ (H ż )
Sż
=
U µ. p (H ż )
Rµ . p ⋅ S ż
=
Θ − H ż ⋅ lż
Rµ . p ⋅ S ż
Bż
Θ
(rys. obok).
Bż (Hż)
Rµ .p⋅ Sż
Punkt przecięcia charakterystyk Bż(Hż) i Bp’ (Hż) wyznacza
Bż
Bp’ (Hż)
szukaną wartość indukcji magnetycznej Bż , stąd Φ = B ż ⋅ S ż .
Hż
0
Hż
Θ
1,4
1806
1,5
2846
Jeśli zależność nieliniowa Bż (Hż) dana jest w postaci numerycznej,
lż
to zwykle wyznacza się charakterystykę wypadkową Φ (Θ ), też w postaci numerycznej.
1 Φ
Dla wartości Bż i Hż oblicza się wartości: Φ = B ż ⋅ S ż , Θ = U µ.ż + U µ. p = H ż ⋅ l ż + ⋅ ⋅ l p .
µ0 S p
Szukaną wartość Φ, przy danej wartości Θ, wyznacza się dokładnie na zasadzie interpolacji.
Obliczanie wartości Θ, przy danych wartościach Bż lub Φ, jest dużo łatwiejsze, albowiem punktem
wyjścia jest wielkość, do której bezpośrednio odnosi się związek nieliniowy.
W powyższych rozważaniach pominięto wpływ grubości płytek na rdzeniu przy szczelinie powietrznej, ustalających powierzchnię jej przekroju (jeśli jest ona różna od powierzchni przekroju rdzenia).
Przykład. W rdzeniu stalowym ze szczeliną powietrzną o danych: Sż = Sp = 25 cm2, lż = 120 cm,
lp = 2 mm, uzwojenie wytwarza przepływ Θ = 2600 A. Szukana jest wartość strumienia Φ.
Charakterystyka magnesowania rdzenia jest zadana numerycznie:
B (T)
H (A/m)
0,5
299
0,6
359
0,7
423
0,8
488
0,9
568
1,0
668
1,1
812
1,2
1002
1,3
1317
1,6
5134
Wyznacza się wartości Φ i Θ dla spodziewanego fragmentu wypadkowej charakterystyki Φ (Θ ), po
czym znajduje wartości skrajne przedziałów, w którym są wartości: zadana Θ i szukana Φ.
B (T) H (A/m) Φ (10-3 Wb)
Θ (A)
Obliczenie wartości Φ dla Θ = 2600 A:
0,8
0,9
1,0
1,1
488
568
668
812
2,00
2,25
2,50
2,75
1811
2114
2393
2725
2600 − 2393
≅ 2,656 ;
2725 − 2393
Φ = 2,656⋅10-3 Wb .
2,5 + (2,75 − 2,5) ⋅
Obwód magnetostatyczny rozgałęziony
Przykład. W rdzeniu stalowym ze szczeliną powietrzną (rys.) o danych: S1 = S2 = Sp = 25 cm2,
S3 = 10 cm2, l1 = l2 = 60 cm, l3 = 40 cm, lp = 2 mm, uzwojenie wytwarza przepływ Θ = 2600 A. Szukana jest wartość indukcji Bp . Charakterystyka magnesowania rdzenia jest zadana numerycznie (jw.).
Φ p = B p ⋅ S p = Φ 2 ; B2 = B p → H2 ;
Φ1 Φ2 (Rµ .2)
l1
Φ2
Φ1
l2 /2
U µ 3 = U µ 2 + U µ. p = l 2 ⋅ H 2 + l p ⋅ B p µ 0 ;
Uµ 1 Φ3 Uµ 2
Φ3
(Rµ .1)
H 3 = U µ3 l3 → B3 ; Φ 3 = B3 ⋅ S 3 ;
Θ
lp
Uµ 3
l3
Uµ .p
Θ
Φ = Φ + Φ ; B = Φ S → H1 ;
l2 /2
(Rµ .3)
1
Rµ .p
Bp (T)
0,6
0,7
0,8
0,77
Φp (mWb) H2 (A/m) Uµ3 (A) H3 (A/m)
1,50
1,75
2,00
359
423
488
3
p
1
1
1
Θ = U µ1 + U µ3 = l1 ⋅ H1 + U µ3 .
B3 (T) Φ1 (mWb)
1170
2925
1,503
3,00
1368
3420
1,525
3,28
1566
3915
1,547
3,55
← wynik interpolacji
B1 (T)
1,20
1,31
1,42
H1 (A/m)
1002
1366
2014
Θ (A)
1771
2188
2774
2600