Laboratorium modelowania symulacyjnego

Politechnika Wrocławska, Wydział Informatyki i Zarządzania, Zarządzanie
LABORATORIUM MODELOWANIA SYMULACYJNEGO
Temat: "SYMULACJA CIĄGŁA - Metoda Dynamiki Systemów"
”ZASOBY I STRUMIENIE”
ELEMENTY MODELI SD
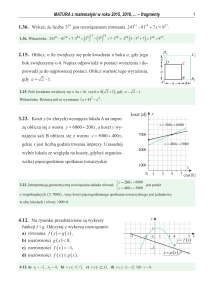
Notacja graficzna
Zasob
X
Z
b
a
Definicja i przykłady
Zasób (ang. stock) – akumulacja (suma) pewnego medium
(fizycznego lub niefizycznego, która zmienia się w czasie (rośnie
lub maleje). W modelu systemu jest to zmienna akumulacyjna
określająca stan systemu w danej chwili. Matematyczna
interpretacja: całka różnicy strumieni. W metodzie SD jest to
„rzeczownik”. Przykłady:
a) woda w zbiorniku,
b) zapas towaru w magazynie,
c) pieniądze na koncie w banku,
d) chorzy ludzie,
e) motywacja do pracy,
f) wiedza.
Strumień (ang. flow) – zmiana, działanie, proces lub decyzja,
które bezpośrednio wpływają na zmianę zasobu. Strumień może
być strumieniem wejściowym (ang inflow) lub strumieniem
wyjściowym (ang outflow). W modelu systemu jest to zmienna
określająca przepływ medium w danym przedziale czasu.
Matematyczna interpretacja: pierwsza pochodna zasobu po
czasie. W metodzie SD jest to „czasownik”. Przykłady:
a) dopływ lub odpływ wody do/z zbiornika,
b) przyjęcia lub wydania towaru do/z magazynu,
c) wpłaty na konto lub wypłaty z konta,
d) zachorowania lub wyleczenia,
e) wzrost lub spadek motywacji,
f) uczenie się lub zapominanie wiedzy.
Wielkość pomocnicza (ang. converter, auxiliary) – wielkość
określająca stan informacji pomocniczej lub zależności, mającej
wpływ na strumień lub na inną wielkość pomocniczą. Może to
być wielkość stała lub zmienna. Przykłady:
a) pożądany poziom wody w zbiorniku,
b) pożądany zapas towaru w magazynie,
c) oprocentowanie bankowe,
d) skuteczność antybiotyka,
e) tempo wzrostu lub spadku motywacji,
f) tempo (czas) uczenia się lub zapominania.
Zależność relacyjna (ang. connector) – relacja przyczynowoskutkowa pomiędzy dwoma elementami. Możliwe są
następujące relacje: zasób-strumień, zasób-zmienna
pomocnicza, strumień-strumień, strumień-zmienna pomocnicza,
zmienna pomocnicza-strumień, zmienna pomocnicza-zmienna
pomocnicza, stała-zmienna pomocnicza, stała-strumień.
Politechnika Wrocławska, Wydział Informatyki i Zarządzania, Zarządzanie
LABORATORIUM MODELOWANIA SYMULACYJNEGO
Temat: "SYMULACJA CIĄGŁA - Metoda Dynamiki Systemów"
ĆWICZENIE NR 1 (Wartość majątku produkcyjnego)
Zbuduj model symulacyjny odwzorowujący zmiany wartości majątku produkcyjnego. Wartość majątku
produkcyjnego w danej chwili jest skumulowaną różnicą pomiędzy przyrostem majtku w wyniku inwestycji a
spadkiem jego wartości w wyniku amortyzacji. W ciągu roku firma wprowadzając nowe inwestycje powiększa o
5% wartość majątku (tempo inwestycji TI=0.05 [1/rok]), natomiast w tym samym czasie majątek 3% wartości
poprzez amortyzację (tempo amortyzacji TA=0.03 [1/rok]). Początkowa wartość majątku jest równa MA(0)=25
[mln zł]. Wykonaj schemat strukturalny oraz zaproponuj równania modelu. Podaj warunek równowagi
dynamicznej modelu. Wykonaj badania symulacyjne wpływu tempa inwestycji i amortyzacji na wartość majątku
oraz określ typy zachowań systemu. Wskazówka: metoda SD, narzędzia – Vensim PLE (lub IThink), złożoność
modelu – 3 zmienne, 2 stałe.
ĆWICZENIE NR 2 (Regulacja zapasów w logistyce)
Zbuduj model symulacyjny opisujący dynamikę zmian w systemie zapasów z regulacją stanu zapasów
magazynowych w oparciu o ujemne sprzężenie zwrotne 1. rzędu. Stan początkowy magazynu wynosi 200 palet
a pożądany stan w magazynie wynosi 250 palet. Zamówienia dostaw do magazynu realizowane są w czasie 2
dni a wydania z magazynu są realizowane w czasie 1 dnia na podstawie zamówienia przesłanego przez klientów
magazynu. Zamówienia klientów wahają się w przedziale od 10 do 100 palet i opisane są pewną funkcją
graficzną Wykonaj badania symulacyjne w celu określenia wpływu zmian wielkości stałych modelu na
zachowanie się systemu. Wskazówka: metoda SD, narzędzia – Vensim PLE (lub IThink), złożoność modelu – 5
zmiennych, 3 stałe.
ĆWICZENIE NR 3 (Ekosystem z jednym gatunkiem zwierząt)
W środowisku naturalnym o ograniczonym obszarze żyje pewien gatunek zwierzęcia. Liczebność populacji tego
gatunku kształtowana jest przez procesy urodzin i śmierci tego gatunku. Przewaga urodzin nad śmiertelnością z
przyczyn naturalnych daje szybkość wzrostu równą a  N , gdzie N jest bieżącą liczbą zwierząt. Niedostatek
2
pożywienia powoduje śmierć głodową z częstotliwością b  N . Zbuduj model symulacyjny opisujący dynamikę
5
zmian liczebności tego gatunku zwierząt zakładając, że a  0.05 , b  1  10 , a chwili początkowej N  500 .
Wykonaj schemat przyczynowo-skutkowy, schemat strukturalny oraz podaj równania modelu. Określ na
podstawie analizy struktury (sprzężeń zwrotnych) postać zachowania się odwzorowanego systemu. Podaj
warunek równowagi dynamicznej systemu. Wykonaj badania symulacyjne wpływu charakterystyk gatunkowych
na kształtowanie się liczebności gatunków. Wskazówka: metoda SD, narzędzia – Vensim PLE (lub IThink),
złożoność modelu – 3 zmienne, 2 stałe.
ĆWICZENIE NR 4 (Ekosystem „Drapieżnik-ofiara”)
W środowisku naturalnym żyją dwa gatunki biologiczne, z których jeden nazywany "drapieżnikiem" (np. lis) żywi
się drugim, nazywanym "ofiarą" (np. zając). Liczebność gatunku ofiary ma wpływ na przyrost liczebności
(rozrodczość) gatunku drapieżnika. Z kolei liczebność gatunku drapieżnika ma wpływ na zmniejszanie się
liczebności gatunku ofiary. Przyjmuje się założenie, że dany ekosystem ma charakter zamknięty (brak procesów
przemieszczania się gatunków). Procesy rozmnażania gatunku ofiary oraz wymierania gatunku drapieżnika mają
charakter naturalny (określone tempo urodzeń i tempo zgonów). Tempo urodzeń rocznych w populacji ofiary
wynosi 0.3 (populacja powiększa się o 30%). Jeden drapieżnik w ciągu roku zabija osobniki gatunku ofiary z
tempem 0.002 (roczny spadek populacji ofiary o 2‰). Tempo zgonów rocznych w populacji drapieżnika wynosi
0.3 (populacja zmniejsza się o 30%). Jeden osobnik gatunku ofiary wpływa z tempem 0.001 na urodzenia roczne
w populacji drapieżnika (roczny przyrost urodzeń w populacji drapieżnika o 1‰). Zbuduj model symulacyjny
opisujący dynamikę zmian liczebności gatunkowych. Określ warunek równowagi dynamicznej modelu (systemu).
Wykonaj badania symulacyjne wpływu charakterystyk gatunkowych na kształtowanie się liczebności gatunków.
Wskazówka: metoda SD, narzędzia – Vensim PLE (lub IThink), złożoność modelu – 6 zmiennych, 4 stałe.
ĆWICZENIE NR 5 (Produkcja i zapasy)
Strategia produkcyjna pewnej firmy produkcyjnej polega na dostosowaniu zapasów wyrobów gotowych w
magazynie do stanu pożądanego oraz utrzymaniu stanu zapasów na odpowiednio wysokim poziomie w
przewidywaniu przyszłego popytu. W celach bezpieczeństwa firma zamierza utrzymywać zapas awaryjny równy
dwukrotnej wartości popytu oczekiwanego. Wielkość natężenia produkcji ustalona jest jako cotygodniowa
korekta 1/2 różnicy pomiędzy pożądanym a bieżącym zapasem. Prognoza popytu (popyt oczekiwany) określana
jest na podstawie zmiany popytu bieżącego (rzeczywistego) z korektą w każdym tygodniu 1/5 różnicy pomiędzy
popytem rzeczywistym a oczekiwanym. Kiedy zmienia się wartość popytu oczekiwanego, powoduje to zmianę
pożądanego poziomu zapasów oraz zmianę natężenia produkcji, zgodnie z przyjętą strategią produkcyjną. Po
wyprodukowaniu produkt firmy jest przesyłany do magazynu. Realizacja dostawy do klientów (wysyłka) jest
Politechnika Wrocławska, Wydział Informatyki i Zarządzania, Zarządzanie
dokonywana z magazynu na podstawie popytu bieżącego, opisanego pewną funkcją graficzną. Zbuduj model
symulacyjny oraz wykonaj eksperymenty symulacyjne badania wpływu zamówień odbiorcy oraz występujących
opóźnień na produkcję i stan zapasów. Wskazówka: metoda SD, narzędzia – Ithink lub Vensim, szacunkowa
złożoność modelu – 7 zmiennych, 3 stałe.
ĆWICZENIE NR 6 (Urządzenia klimatyzacyjne)
Firma Y produkuje urządzenia klimatyzacyjne do budowanych przez deweloperów domów jednorodzinnych.
Natężenie sprzedaży domów jednorodzinnych zależy od liczby rodzin nie posiadających jeszcze domu. Wraz ze
zmniejszaniem się liczby rodzin nie posiadających domu maleje natężenie ich sprzedaży. Natężenie sprzedaży
urządzeń klimatyzacyjnych zależy od liczby zbudowanych domów i maleje wraz ze zmniejszaniem się
niezaspokojonego popytu. Opóźnienie pomiędzy potencjalnym popytem na domy a ich sprzedażą wynosi T1.
Opóźnienie pomiędzy sprzedażą domów a sprzedażą urządzeń klimatyzacyjnych wynosi T2. Urządzenia
klimatyzacyjne zużywają się (po zużyciu są złomowane). Przeciętny czas życia urządzenia klimatyzacyjnego
wynosi T3. Zatem część N [%] właścicieli domów staje się po pewnym czasie T4 ponownie potencjalnymi
klientami firmy Y. Prawdopodobnie w najbliższym czasie nastąpi wzrost oprocentowania kredytu hipotecznego
na zakup domu skutkujący zmniejszeniem popytu na domy o 10%. Firma chce sprawdzić wpływ skokowego
wzrostu oprocentowania kredytu hipotecznego na sprzedaż domów oraz sprzedaż urządzeń klimatyzacyjnych
zakładając, że przeciętny czas potrzebny na sprzedaż domu wynosi 5 miesięcy, przeciętny czas na
zainstalowanie klimatyzacji wynosi 10 miesięcy, zużycie następuje przeciętnie po 25 miesiącach, 90% klientów
decyduje się na ponowną instalację urządzenia firmy Y, opóźnienie instalacji nowego urządzenia po zużyciu
poprzedniego wynosi 2 miesiące, a początkowa liczba potencjalnych nabywców domów wynosi 1000. Wykonaj
schemat przyczynowo-skutkowy, schemat strukturalny oraz podaj równania modelu. Określ na podstawie analizy
struktury (sprzężeń zwrotnych) typ zachowania się odwzorowanego systemu. Czy sprzedaż urządzeń
klimatyzacyjnych może mieć charakter funkcji oscylacyjnej? Wykonaj schemat przyczynowo-skutkowy, schemat
strukturalny oraz podaj równania modelu. Określ na podstawie analizy struktury (sprzężeń zwrotnych) oraz
wykonanego eksperymentu symulacyjnego typy zachowania się odwzorowanego systemu. Wskazówka: metoda
SD, narzędzia – Vensim PLE (lub IThink).
ĆWICZENIE 7 (Proces instalacji i napraw)
Firma NetSat instaluje i naprawia zestawy do odbioru telewizji satelitarnej (antena, odbiornik). Zatrudnia ono siłę
roboczą wykwalifikowaną zarówno do instalacji, jak i naprawy zestawów. Zestawy są instalowane i naprawiane z
natężeniem proporcjonalnym do liczby pracowników wyznaczonych do instalowania i naprawiania. Po
zainstalowaniu zestaw (antena lub odbiornik) ulega uszkodzeniu po pewnym znanym (przeciętnym) czasie
eksploatacji. Zarząd firmy stara się kierować jak najwięcej ludzi do prac instalacyjnych. Dla zachowania
równowagi kieruje on ludzi do prac naprawczych z natężeniem proporcjonalnym do liczby uszkodzonych
zestawów. Naprawa trwa pewien (przeciętny) czas, po którym pracownicy powracają do prac instalacyjnych.
Zbuduj model symulacyjny funkcjonowania tego przedsiębiorstwa i realizacji procesu instalacji i napraw (wykonaj
schemat przyczynowo-skutkowy, schemat strukturalny oraz zaproponuj równania modelu). Wskazówka: zastosuj
metodę Dynamiki Systemów (narzędzia informatyczne: Ithink/Vensim).