Piotr Posmykiewicz – Wykład z fizyki
1
Wykład 17
17.1 Prąd elektryczny, natężenie i gęstośd prądu.
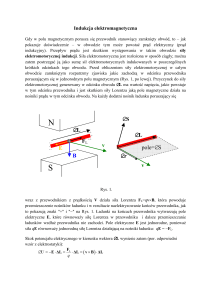
Prądem elektrycznym nazywamy dowolny, uporządkowany (skierowany) ruch ładunków
elektrycznych. Jeżeli w przewodniku podtrzymywad zewnętrzne pole elektryczne 𝑬, to
swobodne ładunki zaczną się w nim przemieszczad: dodatnie – zgodnie z polem, ujemne –
przeciwnie do kierunku pola - mówimy wtedy, że w przewodniku płynie prąd.
Dla powstania i istnienia prądu konieczne jest, z jednej strony, istnienie swobodnych
nośników prądu – naładowanych cząstek, a z drugiej strony, obecnośd pola elektrycznego,
którego energia była by wykorzystana do utrzymania
ładunków w ruchu. Za kierunek prądu przyjmuje się
kierunek ruchu dodatnich ładunków.
Przyjrzyjmy się dokładniej co się dzieje, jeżeli przyłożyd
stałe pole 𝑬 do przewodnika. Naładowana cząstka (taka jak
elektron) zacznie się poruszad pod wpływem działania na nią
stałej siły 𝑭 = 𝑞𝑬. Taka cząsteczka w trakcie swojego ruchu
będzie podlega częstym zderzeniom z masywnymi jonami
Rysunek 17.1
przewodnika. Podczas tych zderzeo kierunek ruchu cząsteczki będzie ulegał gwałtownym
zmianom. Wypadkowe działanie pola elektrycznego sprowadzi się do tego, że cząsteczki
oprócz chaotycznego ruchu między zderzeniami będą poruszad się ze stosunkowo małą
wypadkową prędkością w kierunku działającej siły 𝑭 = 𝑞𝑬 (Rysunek 2.1). Prędkośd tego
ruchu nazywamy prędkością dryfu (unoszenia) cząsteczek 𝐯𝐝 .
Średnia prędkośd chaotycznego ruchu naładowanych cząsteczek jest duża rzędu 106m/s,
podczas gdy prędkośd dryfu dla typowych natężeo prądu jest rzędu 10 -4m/s. Może się to
wydawad na pierwszy rzut oka dziwne w konfrontacji z naszym codziennym doświadczeniem
pokazującym, że natychmiast po wciśnięciu włącznika zapala się światło. Dzieje się tak
dlatego, że pole elektryczne w przewodach rozprzestrzenia się z prędkością porównywalną z
prędkością światła w próżni, a to oznacza, iż elektrony zostaną wprawione w ruch wzdłuż
całego przewodu w praktycznie w jednej chwili.
Piotr Posmykiewicz – Wykład z fizyki
2
Dryf naładowanych cząsteczek w przewodniku można rozpatrywad w pojęciach pracy i
energii. Pole elektryczne 𝑬 wykonuje pracę nad poruszającymi się ładunkami, w wyniku
czego uzyskują one energię kinetyczną. Energia ta przekazywana jest do materiału
przewodnika poprzez zderzenia z jonami, które drgają wokół swych położeo równowagi w
węzłach siatki kryształu. Przekazywana energia zwiększa średnią energię tych drgao i tym
samym temperaturę przewodnika. A zatem większośd pracy wykonanej przez pole idzie na
ogrzewanie przewodnika, a nie na zwiększanie prędkości nośników ładunku. Ciepło to
czasami jest pożyteczne jak na przykład w czajniku elektrycznym, jednak najczęściej jest
nieuniknionym dodatkiem towarzyszącym przepływowi prądu.
W zależności od rodzaju przewodnika przewodzącego prąd
nośnikami mogą byd ładunki dodatnie i ujemne. W metalach
nośnikami ładunku są zawsze elektrony, podczas gdy w
zjonizowanych gazach (plazmie) lub w roztworach jonowych
nośnikami mogą byd zarówno elektrony jak i dodatnie jony.
Rysunek
17.2
przedstawia
dwa
odcinki
różnych
przewodzących materiałów. Na rysunku 17.2a poruszającymi
się cząsteczkami w kierunku pola są dodatnie ładunki i
prędkośd dryfu 𝐯𝐝 jest skierowana z lewa na prawo. Na
rysunku 17.2b poruszają się ładunki ujemne w kierunku
przeciwnym do pola
Rysunek 17.2
i prędkośd dryfu 𝐯𝐝 skierowana jest z prawa na
lewo. W każdym z tych przypadków mamy do
czynienia z wypadkowym przepływem ładunków
dodatnich z lewa na prawo. Kierunek prądu
definiuje się umownie jako kierunek przepływu
ładunków dodatnich. Dlatego też kierunek prądu I
na obu rysunkach 17.2a i 17.2b jest taki sam.
Wprowadza
się
umowny
kierunek
prądu
i
przyjmuje się, że jest on spowodowany dodatnimi
ładunkami, nawet jeżeli rzeczywisty przepływ
Rysunek 17.3
związany jest z ruchem elektronów.
Rysunek 17.3 przedstawia odcinek przewodnika, w którym płynie prąd. Miarą ilościową
prądu elektrycznego jest natężenie prądu elektrycznego I. I jest fizyczną wielkością skalarną
Piotr Posmykiewicz – Wykład z fizyki
3
określającą wielkośd ładunku przechodzącego przez poprzeczny przekrój przewodnika w
jednostce czasu:
𝐝𝐐
𝐈=
17.1
𝐝𝐭
Definicja natężenia prądu.
Prąd, którego natężenie i kierunek nie zmienia się w czasie nazywamy stałym. Jednostką
natężenia prądu jest amper (A = 1C/s).
Przeanalizujmy sytuację przedstawioną na rysunku 17.3. Mamy przewodnik o przekroju
poprzecznym A, pole 𝐄 skierowane na prawo, a nośnikami ładunku są ładunki dodatnie.
Niech w jednostce objętości znajduje się n ładunków. n nazywamy koncentracją i w układzie
SI jej jednostką jest jeden przez m3. Załóżmy, że wszystkie ładunki poruszają się z prędkością
dryfu vd. W przedziale czasu dt każda cząstka przebędzie drogę vddt. Cząstki, które wypływają
z prawej podstawy zacienionego cylindra o długości vddt są cząstkami, które były wewnątrz
cylindra na początku przedziału czasu dt. Objętośd tego cylindra jest równa Av ddt, a ilośd
cząsteczek zawarta w nim wynosi nAvddt. Jeżeli każda cząsteczka posiada ładunek q, to
ładunek, który wypłynie z prawej strony cylindra w czasie dt będzie równy:
𝑑𝑄 = 𝑞 𝑛𝐴𝑣𝑑 𝑑𝑡 = 𝑛𝑞𝑣𝑑 𝐴𝑑𝑡,
a prąd będzie równy:
𝐼=
𝑑𝑄
𝑑𝑡
= 𝑛𝑞𝑣𝑑 𝐴.
Gęstością prądu nazywamy fizyczną wielkośd określoną przez natężenie prądu
przepływającego przez jednostkę powierzchni przekroju przewodnika prostopadłą do
kierunku prądu:
𝐼
𝐽 = 𝐴 = 𝑛𝑞𝑣𝑑
Jeżeli poruszającymi się ładunkami są ładunki ujemne, a nie dodatnie, jak na rysunku
17.2b, wtedy prędkośd dryfu jest przeciwna do kierunku pola 𝐄. Jednak prąd będzie mied
ciągle ten sam kierunek jak 𝐄 w każdym punkcie przewodnika. W związku z tym natężenie
prądu I i gęstośd prądu J nie zależą od znaku ładunku i w związku z tym w wyrażeniach na I i J
q możemy zamienid na q :
𝐈=
𝐝𝐐
𝐝𝐭
= 𝐧 𝐪 𝐯𝐝 𝐀
Ogólne wyrażenie na natężenie prądu.
17.2
Piotr Posmykiewicz – Wykład z fizyki
4
𝐈
𝐉 = 𝐀 = 𝐧 𝐪 𝐯𝐝
17.3
Ogólne wyrażenie na gęstośd prądu.
Gęstośd prądu jest wektorem skierowanym tak jak przepływ prądu, tzn. zwrot wektora j
pokrywa się z kierunkiem uporządkowanego ruchu ładunków dodatnich.
𝐉 = 𝐧𝐪𝐯𝐝
17.4
Wektor gęstości prądu.
Jednostką gęstości prądu jest amper na metr kwadrat (A/m2).
17.2 Prawo Ohma. Opór przewodników.
Niemiecki fizyk Georg Simon Ohm dowiódł eksperymentalnie, że natężenie prądu I
płynącego przez jednorodny metalowy przewodnik (tj. przez przewodnik, w którym nie
występują siły uboczne) jest proporcjonalne do napięcia na koocach tego przewodnika
(Rysunek 17.4):
𝐔
𝐈=𝐑
17.5
Prawo Ohma.
gdzie R jest współczynnikiem proporcjonalności zwanym oporem przewodnika. Równanie
17.5 przedstawia prawo Ohma dla jednorodnego odcinka obwodu:
Natężenie prądu w przewodniku jest wprost proporcjonalna do przyłożonego
napięcia i odwrotnie proporcjonalna do oporu przewodnika.
Wzór 17.5 pozwala określid jednostkę oporu – om (Ω): 1Ω jest to opór takiego
przewodnika, w którym przy napięciu 1V płynie prąd 1A.
Wielkośd G = 1/R nosi nazwę przewodnictwa elektrycznego przewodnika. Jednostką
przewodnictwa jest simens (S),równy 1/Ω.
Opór przewodnika zależy od jego rozmiarów i kształtu, a także od materiału, z którego
zrobiony jest przewodnik. Dla przewodnika o kształcie cylindrycznym opór przewodnika jest
równy:
𝐋
𝐑 = 𝛒𝐀
17.6
gdzie ρ jest współczynnikiem proporcjonalności nazywanym oporem właściwym i zależy on
od rodzaju materiału. Jednostką oporu właściwego jest 1Ωm. Najmniejszy opór właściwy
posiada srebro ( 1,6 108 m ) i miedź ( 1,7 108 m ). W praktyce, oprócz przewodów
Piotr Posmykiewicz – Wykład z fizyki
5
miedzianych stosuje się przewody aluminiowe, chociaż
aluminium posiada większy opór właściwy ( 2,6 108 m ), to
ma mniejszą gęstośd w porównaniu z miedzią.
Niższy
potencjał
R
Wyższy
potencjał
Prawo Ohma można przedstawid w postaci różniczkowej.
U
Załóżmy, że dany jest przewód o polu przekroju A i długości L
(Rysunek 17.4). Niech U będzie różnicą potencjałów między
koocem o wyższym potencjale i koocem o niższym potencjale
Rysunek 17.4
(U > 0). Wtedy podstawiając wyrażenie na opór 17.6 do prawa Ohma (17.5) otrzymujemy:
I 1U
17.7
S ρL
gdzie 𝛄 = 𝟏/𝛒 nazywa się przewodnością właściwą materiału przewodnika. Uwzględniając,
że U/L = E – natężenie pola elektrycznego w przewodniku, I/S = J – gęstośd prądu, wzór 17.7
można zapisad w postaci:
J = γE
17.8
Ponieważ nośniki prądu w każdym punkcie poruszają się w kierunku wektora 𝐄, to kierunki
𝐉 i 𝐄 pokrywają się. Dlatego powyższy wzór można zapisad w postaci wektorowej
𝐉 = 𝛄𝐄
17.9
Prawo Ohma w postaci różniczkowej.
Prawo to jest również słuszne dla prądów zmiennych.
Dla szeregowego połączenia oporów ich opory dodają się:
R = R1 +R2 +...+Rn
A dla równoległego połączenia odwrotnośd oporu całkowitego jest równa sumie
odwrotności poszczególnych oporów:
1/R = 1/R1+1/R2+...+1/R
Wykaż prawdziwośd dwu ostatnich wzorów.
Opór metali prawie zawsze wzrasta wraz ze wzrostem temperatury jak pokazuje to
rysunek 17.5a. W miarę jak wzrasta temperatura jony przewodnika drgają z coraz większą
amplitudą i zderzenia elektronów z nimi stają się coraz bardziej prawdopodobne;
wyhamowuje to dryf elektronów w przewodniku, a tym samym powoduje zmniejszenie
natężenia prądu. Doświadczenie pokazuje, że w małych przedziałach temperatur (od 00C do
Piotr Posmykiewicz – Wykład z fizyki
6
około 1000C) opór właściwy, a co za tym idzie opór przewodników
Nachylenie
= ρ0α
(metali) zmieniają się liniowo wraz z temperaturą:
𝝆 𝑻 = 𝝆𝟎 𝟏 + 𝜶 𝑻 − 𝑻𝟎
𝑹 𝑻 = 𝑹𝟎 𝟏 + 𝜶 𝑻 − 𝑻𝟎
a. Metal
gdzie: ρ i ρ0, R i R0 odpowiednio oporności właściwe i opory w
temperaturach T i T0 (T0 często przyjmuje się równą 00C lub 200C),
α – temperaturowy współczynnik oporu. Współczynnik α zmienia
się w granicach od 0,00001(0C)-1 dla konstantanu do 0.0050(0C)-1
b. Półprzewodnik
dla żelaza.
Opornośd grafitu (nie metalu) zmniejsza się wraz ze wzrostem
temperatury, ponieważ w wyższych temperaturach więcej
elektronów „uwalnia się” od atomów i może poruszad się w
objętości
próbki
grafitu.
Podobne
zjawisko
zachodzi
w
c. Nadprzewodnik
półprzewodnikach (Rysunku 17.5b), przy czym bardzo niewielkie
Rysunek 17.5
zmiany temperatury powodują istotne zmiany oporu.
Jakościowa zależnośd oporu przewodnika od temperatury jest przedstawiona na Rysunku
17.5a. Odkryto jednak, że opór wielu metali (np. Al., Pb, Zn, i innych) i ich stopów w bardzo
niskich
temperaturach
Tk
(0,14-20K)
zwanych
krytycznymi
(Rysunek
17.5c),
charakterystycznych dla każdej substancji, skokowo maleje do zera!, tzn. metal staje się
przewodnikiem idealnym. Po raz pierwszy zjawisko to, zwane nadprzewodnictwem, było
odkryte przez Kammerlingha – Onnesa w 1911roku w rtęci. Zjawisko nadprzewodnictwa daje
się wyjaśnid na gruncie teorii kwantowej. Obecnie (2003) otrzymywane są materiały
nadprzewodnikowe z temperaturą krytyczną około 160K i trwają poszukiwania materiałów,
które byłyby nadprzewodnikami w temperaturach pokojowych. Korzyści tego typu odkryd
dla systemów przesyłania energii, komputerów, transportu wydają się ogromne. Jak na razie
nadprzewodniki stosuje się elektromagnesach chłodzonych ciekłym helem, które są używane
w akceleratorach cząstek i w eksperymentalnych liniach pociągów lewitujących na poduszce
magnetycznej nad torem jazdy.
Na zależności oporu elektrycznego od temperatury oparte jest działanie termometrów
oporowych, które pozwalają zmierzyd temperaturę z dokładnością do 0,003K. Jednak
wykorzystanie jako substancji roboczej w termometrze półprzewodników, przygotowanych
Piotr Posmykiewicz – Wykład z fizyki
7
w specjalny sposób tzw. termistorów, pozwala mierzyd temperaturę z dokładnością do
milionowych części kelvina i umożliwia pomiary temperatury bardzo małych obiektów (ze
względu na małe rozmiary półprzewodników).
17.3 Siły uboczne. Siła elektromotoryczna.
Jeżeli dwa różnoimienne
Kierunek prądu I
V2
przewodniki A i B naładowad
V1
do potencjałów V1 i V2 i
połączyd
(Rysunek
przewodnikiem
17.6)
to,
C
C
A
pod
B
Siła uboczna
wpływem pola zacznie się
przemieszczanie
wzdłuż
ACB,
elektronów
tzn.
Rysunek 17.6
wzdłuż
przewodnika zacznie płynąd prąd w kierunku BCA. W czasie przepływu prądu będzie
zachodzid wyrównywanie się potencjałów i natężenie pola wewnątrz przewodnika zmaleje
do zera i prąd przestanie płynąd.
W celu podtrzymania stałego prądu w przewodniku należałoby mied specjalne
urządzenie, wewnątrz którego zachodziłoby ciągłe rozdzielanie różnoimiennych ładunków i
przenoszenie ich do odpowiednich przewodników (ładunki dodatnie do przewodnika B, a
ujemne do przewodnika A). Takie urządzenie zwane źródłem prądu (lub generatorem)
powinno
działad
na
elektrony
(lub
ogólnie
na
ładunki)
siłami
pochodzenia
nieelektrostatycznego. Siły pochodzenia nieelektrostatycznego działające na ładunki w
źródłach prądu nazywamy ubocznymi.
Natura sił ubocznych może byd różna. Na przykład, w bateriach galwanicznych siły te
powstają dzięki energii reakcji chemicznych między elektrodami a elektrolitami; w
generatorach prądu stałego dzięki energii pola magnetycznego i energii mechanicznej
obracającego się rotora itp. Rola źródła prądu w obwodzie elektrycznym jest taka jak,
mówiąc obrazowo, rola pompy, która jest konieczna do przepompowania cieczy w układzie
hydraulicznym. Dzięki powstałemu polu sił ubocznych, ładunki elektryczne wewnątrz źródła
poruszają się w kierunku przeciwnym do kierunku pola elektrostatycznego i dzięki temu na
koocach obwodu zewnętrznego podtrzymywana jest różnica potencjałów i w obwodzie
płynie stały prąd elektryczny.
Piotr Posmykiewicz – Wykład z fizyki
8
Siły uboczne przesuwając ładunki wykonują pracę. Wielkośd fizyczna określona pracą
wykonaną przez siły uboczne podczas przenoszenia jednostki dodatniego ładunku nazywa się
siłą elektromotoryczną (SEM) E działającą w obwodzie:
𝓔=
𝐖𝐮
17.10
𝐐𝟎
Siła ElektroMotoryczna (SEM).
Praca ta jest wykonana kosztem energii traconej w źródle prądu. Jednostką SEM jest volt (1V
=J/C).
Rysunek 17.7 przedstawia schemat idealnego źródła SEM, które utrzymuje stałą różnicę
potencjałów między przewodnikami a i b zwanymi biegunami źródła.
Biegun a oznaczony + posiada wyższy potencjał niż biegun b
oznaczony - . Z tą różnicą potencjałów związane jest pole elektryczne
𝐄, które znajduje się zarówno wewnątrz jak i na zewnątrz źródła.
u
Rysunek 17.7
Pole elektryczne wewnątrz źródła jest skierowane od a do b. Na
ładunek q wewnątrz źródła działa siła elektryczna Fe = qE. Jednak samo źródło również
wprowadza dodatkowe działanie reprezentowane przez siłę uboczną 𝐅𝐮 . Siła ta działając
wewnątrz źródła wpycha ładunek od b do a w kierunku „do góry” przeciwnie do kierunku
działania siły elektrycznej 𝐅𝐞 . W ten sposób 𝐅𝐮 utrzymuje różnicę potencjałów między
biegunami. Jeżeli nie byłoby siły 𝐅𝐮 ładunek przepływał by między biegunami aż potencjały
wyrównałyby się.
Jeżeli ładunek dodatni jest przenoszony z b do a wewnątrz źródła, wtedy siła uboczna 𝐅𝐮
wykonuje dodatnią pracę Wu = qℰ nad ładunkiem. Takie przemieszczenie odbywa się w
kierunku przeciwnym do siły elektrostatycznej 𝐅𝐞 w związku z czym energia potencjalna
związana z ładunkiem zwiększa się o wartośd qUab, gdzie Uab = Va – Vb jest potencjałem
punktu a(dodatnią) względem punktu b. Dla idealnego źródła SEM opisanego wyżej 𝐅𝐞 i 𝐅𝐮 są
równe co do wartości, ale mają przeciwne zwroty, a zatem całkowita praca wykonana nad
ładunkiem jest równa zero; następuje wzrost energii potencjalnej, a energia kinetyczna
ładunku nie zmienia się. Można to porównad do podnoszenia książki z podłogi na półkę ze
stałą prędkością. Wzrost energii potencjalnej jest równy pracy wykonanej przez siłę uboczną
Wu ; qℰ = qUab , lub
Uab = ℰ
(idealne źródło SEM)
17.11
Piotr Posmykiewicz – Wykład z fizyki
9
Zamknijmy teraz obwód poprzez połączenie biegunów źródła
oporem R (Rysunek 17.8). Różnica potencjałów między
biegunami a i b wytwarza pole elektryczne w przewodniku; a to
u
wywołuje przepływ prądu w pętli z a do b, od wyższego do
niższego potencjału.
Z prawa Ohma wiemy, że różnica potencjałów na koocach
Rysunek 17.8
przewodu jest wynosi Uab = IR. Porównując to z 17.11 otrzymujemy:
ℰ = Uab = IR (idealne źródło SEM)
17.12
Oznacza to, że jeżeli dodatni ładunek q płynie w obwodzie, wtedy wzrost potencjału ℰ przy
przechodzeniu ładunku przez źródło jest równy spadkowi potencjału Uab = IR, kiedy
ładunek przepływa przez pozostałą częśd obwodu. Jeżeli znane są tylko ℰ i R, to znany jest
również prąd I.
Opór wewnętrzny.
Rzeczywiste źródła prądu zachowują się jednak trochę inaczej; różnica potencjałów na
biegunach realnego źródła nie jest równa SEM jak w przypadku 17.12. Powodem tego jest
fakt, że w ładunek przepływając przez normalne źródło prądu napotyka na opór. Opór ten
nazywa się oporem wewnętrznym i oznaczmy go przez r. Przepływowi prądu przez opór
wewnętrzny towarzyszy spadek potencjału Ir. W rezultacie kiedy prąd płynie przez źródło od
bieguna ujemnego b do bieguna dodatniego, wtedy różnica potencjałów między biegunami
wynosi
𝐔𝐚𝐛 = 𝓔 − 𝐈𝐫
17.13
Napięcie na biegunach źródła zamkniętego.
To napięcie jest mniejsze niż SEM ℰ z powodu spadku potencjału na oporze wewnętrznym r.
Można to wyrazid w inny sposób: wzrost energii potencjalnej qU ab ładunku kiedy przechodzi
on z b do a wewnątrz źródła jest mniejszy niż praca wykonana przez siły uboczne qℰ,
ponieważ
częśd
energii
potencjalnej
jest
tracona
podczas
pokonywania
oporu
wewnętrznego.
Bateria półtora – woltowa posiada SEM równą 1,5V, jednak napięcie na zaciskach ogniwa
zamkniętego jest mniejsze.
Prąd płynący w obwodzie zewnętrznym połączonym z biegunami a i b ogniwa jest w
dalszym ciągu określony przez Uab = IR. Łącząc to z 17.14 otrzymujemy:
Piotr Posmykiewicz – Wykład z fizyki
10
ℰ − Ir = IR
lub
ℇ
I = R+r
17.14
Wypadkowa zmiana energii potencjalnej ładunku q pokonującego drogę wzdłuż całego
obwodu zamkniętego musi byd równa zero. W związku z tym wypadkowa zmiana potencjału
wzdłuż całego obwodu też musi byd równa zero; innymi słowy: algebraiczna suma różnic
potencjałów i SEM wokół obwodu musi byd równa zero. Widad to jeżeli przepiszemy
równanie 17.14 w postaci:
ℰ − Ir − IR = 0
Wzrost potencjału o ℰ związany jest z SEM, a spadek potencjału o Ir i IR związany jest z
opornością wewnętrzną i opornością obwodu. Rysunek 17.9 pokazuje jak zmienia się
potencjał w trakcie obchodzenia obwodu. Jeżeli przyjmiemy, że potencjał jest równy zero w
miejscu bieguna ujemnego ogniwa, wtedy mamy
najpierw wzrost potencjału o ℰ i spadek o Ir w
obrębie ogniwa i dodatkowe zmniejszenie potencjału
o IR na oporze zewnętrznym i kiedy kooczymy
obchodzenie obwodu potencjał jest znów równy
początkowemu czyli zero.
Różnica między nową baterią np. 1,5V, a starą
zużytą nie polega na tym, że w starej SEM jest niższa
(zmienia się ona tylko trochę), a na tym, że w starej
opór wewnętrzny zwiększa się znacznie (może on się
zmienid na przykład z 1Ω w nowej baterii do nawet
Rysunek 17.9
1000 Ω w starej). Podobnie akumulator samochodowy może dostarczad mniej prądu w zimny
poranek dlatego, że opór wewnętrzny akumulatora w sposób istotny zależy od temperatury,
wzrastając znacznie przy niskiej temperaturze. Dlatego też czasami stosuje się różnego
rodzaju ocieplacze akumulatorów.
17.4 Praca i moc prądu.
Przeanalizujmy związek zachodzący między energią i mocą w obwodzie elektrycznym.
Niech prostokąt na rysunku 17.10 reprezentuje fragment obwodu elektrycznego, między
koocami którego istnieje napięcie (różnica potencjałów) Uab = Va – Vb przez który, płynie
Piotr Posmykiewicz – Wykład z fizyki
11
Va
prąd I. W fragmencie tym może znajdowad się
zarówno opornik jak i źródło prądu. Gdy ładunek
przepływa
przez
ten
element,
wtedy
Vb
Element obwodu
I
I
siły
a
b
elektrostatyczne 𝐅𝐞 lub (i) siły uboczne 𝐅𝐮 wykonują
pracę nad tym ładunkiem.
Rysunek 17.10
Jeżeli przez ten element obwodu przepłynie ładunek q, wtedy zmiana energii potencjalnej
wyniesie qUab. Na przykład, jeżeli q > 0 i Uab = Va – Vb jest dodatnie, to energia potencjalna
zmaleje, gdy ładunek „spadnie” z potencjału Va na poziom o potencjale Vb. Poruszający się
ładunek nie zwiększy jednak swojej energii kinetycznej, ponieważ prędkośd przepływu
ładunku jest wszędzie taka sama. Zamiast tego qUab będzie energią przekazaną do elementu
obwodu na przykład w postaci energii cieplnej (spirala grzewcza w czajniku elektrycznym).
Może się zdarzyd, że potencjał w b będzie wyższy niż w a. W takim przypadku Uab będzie
ujemne i nastąpi wypływ energii z elementu obwodu. Wtedy taki element działa jak źródło
dostarczając energię do obwodu, do którego jest podłączony. Sytuacja taka jest typowa dla
ogniwa, które przekształca energię chemiczną w energię elektryczną i przekazuje ją dalej do
obwodu zewnętrznego. Zatem qUab może oznaczad zarówno energię dostarczoną do
elementu obwodu, jak i energię wydzieloną z tego elementu.
W przypadku obwodów elektrycznych interesuje nas najczęściej szybkośd z jaką energia
jest dostarczana do elementu obwodu lub wydzielana z niego. Jeżeli prąd płynący przez
element wynosi I, wtedy w czasie dt przez ten element przepłynie ładunek dQ = Idt. Zmiana
energii potencjalnej takiej ilości ładunku będzie równa UabdQ = UabIdt. Dzieląc to wyrażenie
przez dt otrzymamy szybkośd z jaką energia jest przekazywana do lub z danego elementu. Ta
czasowa szybkośd przekazywania energii jest mocą P:
𝐏 = 𝐔𝐚𝐛 𝐈
17.15
Szybkośd z jaką energia przekazywana jest do lub z elementu obwodu.
Jednostką napięcia jest volt, lub dżul na kulomb, a jednostką prądu amper czyli kulomb na
sekundę. Stąd jednostką P jest wat:
(1J/C)(1C/s) = 1J/s = 1W
Jeżeli natężenie prądu wyrażone jest w amperach, napięcie w woltach, a opór w omach,
to praca prądu wyrażona jest w dżulach. Stosuje się również jednostkę pracy
kilowatogodzinę – 1kWh 1kW 1h 1000W 3600s 3,6 106 J .
Piotr Posmykiewicz – Wykład z fizyki
12
Przeanalizujmy szczególne przypadki.
Czysty opór.
Jeżeli elementem obwodu z rysunku 17.10 jest opornik, wtedy różnica potencjałów wynosi
Uab = IR. Zatem moc dostarczona do opornika przez obwód wyniesie na podstawie 17.15:
𝐏 = 𝐔𝐚𝐛 𝐈 = 𝐈𝟐 𝐑 =
𝟐
𝐔𝐚𝐛
17.16
𝐑
Moc dostarczona do opornika.
W tym przypadku potencjał w punkcie a (gdzie prąd wpływa do
opornika) jest zawsze wyższy niż w punkcie b i równanie 17.16
przedstawia
szybkośd
przekazywania
elektrycznej
energii
Ogniwo
potencjalnej do elementu obwodu.
Co dzieje się z tą energią? Poruszające się ładunki zderzają się z
Obwód
zewnętrzny
atomami w oporniku i przekazują częśd swojej energii atomom,
zwiększając tym samym energię wewnętrzną materiału. W wyniku
tego może wzrosnąd temperatura opornika lub ciepło może byd
przekazywane na zewnątrz lub oba te zjawiska mogą zachodzid
Akumulator
równocześnie. W każdym z tych przypadków mówimy, że energia
ulega rozpraszaniu w oporniku z szybkością I2R. Każdy opornik
posiada tzw. moc znamionową, która określa maksymalną moc,
która może byd rozpraszana w oporniku bez spowodowania jego
uszkodzenia.
Reflektor
Rysunek 17.11
Moc wychodząca ze źródła.
Wyższy prostokąt na rysunku 17.11a reprezentuje źródło o SEM ℰ i
oprze wewnętrznym r połączone za pomocą idealnych przewodów
(bezoporowe) z zewnętrznym obwodem reprezentowanym przez
dolny prostokąt. Może byd to schemat połączenia akumulatora
samochodowego z reflektorami (Rysunek17.11b). Punkt a ma wyższy
Akumulator
mała SEM
potencjał niż punkt b, czyli Va > Vb i Uab jest dodatnie. Zwródmy
uwagę, że prąd I wypływa z bieguna o wyższym potencjale (chociaż
może byd odwrotnie). Energia jest dostarczana do obwodu
zewnętrznego, a szybkośd dostarczania tej energii określona jest
wzorem 17.15:
Alternator
duża SEM
Rysunek 17.12
Piotr Posmykiewicz – Wykład z fizyki
13
P = Uab I
Dla źródła, które może byd scharakteryzowane za pomocą SEM ℰ i oporu wewnętrznego r
możemy użyd 17.13:
Uab = ℰ − Ir
W rezultacie otrzymamy:
P = Uab I = ℰI − I2 r
Co oznaczają człony ℰI i I2 r?
jednostkę
ładunku
17.17
Poprzednio zdefiniowaliśmy SEM ℰ jako pracę na
wykonaną
nad
ładunkami
przez
siłę
o
pochodzeniu
nieelektrostatycznym (siłę uboczną) w trakcie ich wpychania „pod górę” od b do a. W
czasie dt ładunek dQ = Idt przepłynie przez źródło; praca wykonana przez siły uboczne
nad tym ładunkiem będzie równa ℰdQ = ℰIdt. Zatem ℰI określa szybkośd z jaką
wykonywana jest
praca nad poruszającymi się ładunkami przez jakiś czynnik
wywołujący siłę uboczną w źródle. Czynnik ten określa szybkość z jaką przekształcana
jest energia nie elektryczna w energię elektryczną w obrębie źródła. Czynnik I2r określa
szybkość z jaką energia jest rozpraszana w oporze wewnętrznym źródła. Zatem różnica
ℰI - I2 r określa wypadkową moc wychodzącą ze źródła – tzn. szybkość z jaką źródło
dostarcza energię elektryczną do pozostałej części obwodu.
Moc wchodząca do źródła.
Załóżmy, że niższy prostokąt z rysunku 17.11a sam jest źródłem posiadającym SEM większą
niż górne źródło i jego SEM włączona jest przeciwnie do źródła górnego. Rysunek 17.12
przedstawia
praktyczny
przykład
–
akumulator
samochodowy
podłączony
do
samochodowego alternatora. Prąd w tym obwodzie płynie w kierunku przeciwnym niż ten z
rysunku 17.11; dolne źródło zmusza prąd do ruchu do tyłu w kierunku górnego źródła. Z
powodu tego prądu o przeciwnym kierunku zamiast równania 17.13 dla górnego źródła
mamy:
Uab = ℰ + Ir ,
a zamiast równania 17.17 otrzymujemy:
P = Uab I = ℰI + I2 r
17.18
Praca w górnym źródle jest wykonana nad czynnikiem wywołującym siły uboczne a nie przez
ten czynnik. W tym wypadku w górnym źródle ma miejsce zamiana energii elektrycznej na
energię nieelektryczną, która zachodzi z szybkością ℰI. Czynnik I2r w równaniu 17.18 jest
ponownie szybkością rozpraszania energii w oporze wewnętrznym górnego źródła, a
suma ℰI + I2 r całkowitą mocą wejściową dla górnego źródła. Taka sytuacja występuje,
Piotr Posmykiewicz – Wykład z fizyki
14
jeżeli podłączyć akumulatorek do ładowarki. Ładowarka dostarcza energię elektryczną
do baterii; część tej energii jest zamieniana na energię chemiczną, które ponownie
później zostanie zamieniona na energię elektryczną, a reszta jest tracona poprzez
rozproszenie jej w oporze wewnętrznym możemy to poczuć, ponieważ akumulatorek w
czasie ładowania nagrzewa się .
17.5 Prawo Joule’a – Lenza.
Wyrażenia 17.16 są prawdziwe zarówno dla prądu stałego jak i zmiennego, przy czym dla
prądu zmiennego należy podstawid do tych wyrażeo wielkości chwilowe.
Jeżeli prąd płynie przez nieruchomy metalowy przewodnik, to cała praca jest tracona na
jego ogrzanie, i z zasady zachowania energii
dQ dW
17.19
Wykorzystując wyrażenia 2.13 otrzymujemy
dQ IUdt I 2 Rdt
U2
dt
R
17.20
Wyrażenia 17.20 przedstawiają prawo Joule’a –Lenza.
Wydzielmy w przewodniku nieskooczenie małą, cylindryczną
objętośd dV = dAdL, której opór wynosi R ρdL/dA . Zgodnie z
prawem Joule’a –Lenza w ciągu czasu dt w objętości tej wydzieli się
dV-objętość
ciepło
dQ I 2 Rdt
dL
ρdl
jdA 2 dt ρj2dVdt
dA
Ilośd ciepła wydzielona w jednostce czasu, w jednostce objętości
𝐝𝐐
jest właściwą mocą cieplną prądu 𝐰 = 𝐝𝐭𝐝𝐕 i jest jak widad równa:
w ρj2
dU
dA
Rysunek 17.13
17.21
Korzystając z różniczkowego prawa Ohma (j = γE) i podstawiając ρ= 1/γ otrzymujemy
w jE γE 2
17.22
Wzory 17.21 i 17.22 wyrażają uogólnione prawo Joule’a - Lenza w postaci różniczkowej,
prawdziwe dla prądu stałego i zmiennego.
17.6 Prawo Ohma dla niejednorodnego odcinka obwodu.
Piotr Posmykiewicz – Wykład z fizyki
15
Rozpatrzmy niejednorodny odcinek obwodu, tzn. taki, w którym na odcinku 1-2
występuje siła elektromotoryczna E12 i na koocach którego, różnica potencjałów wynosi V1 –
V 2.
Jeżeli prąd przepływa przez nieruchomy odcinek 1-2 obwodu, to praca dW12 wszystkich
sił (ubocznych i elektrostatycznych) wykonana nad nośnikami ładunku, zgodnie z zasadą
zachowania energii jest równa ciepłu dQ wydzielonemu w tym odcinku. Ładunek dQ0
przenoszony w czasie dt wzdłuż przewodnika jest równy Idt. Praca sił wykonana przy
przesunięciu tego ładunku na odcinku 1-2 zgodnie z 2.6 wynosi:
𝑑𝑊12 = 𝑑𝑄0 ℇ12 + 𝑑𝑄0 𝑉1 − 𝑉2
17.23
Siła elektromotoryczna ℇ12 jak i natężenie prądu jest wielkością skalarną. Należy ją
przyjmowad albo ze znakiem plus, albo minus w zależności od znaku pracy wykonanej przez
siły uboczne. Jeżeli SEM sprzyja ruchowi dodatnich ładunków w wybranym kierunku ( w
kierunku 1-2), to ℇ12 > 0. Jeżeli SEM przeszkadza w ruchu dodatnich ładunków w wybranym
kierunku to ℇ12 < 0.
W czasie dt w przewodniku wydziela się ciepło dQ:
dQ I2 Rdt IRIdt IRdQ0
17.24
Ze wzorów 17.24 i 17.23 otrzymujemy:
IR = V1 − V2 + ℇ12
17.25
skąd
𝐈=
𝐕𝟏 −𝐕𝟐 +ℇ𝟏𝟐
𝐑
17.26
Prawo Ohma dla niejednorodnego odcinka obwodu, które jest uogólnionym prawem
Ohma.
Jeżeli na danym odcinku obwodu nie ma źródła prądu (ℇ12 = 0), to z 17.26 wynika, że
otrzymujemy prawo Ohma dla jednorodnego odcinka prądu 17.5:
I V1 V2 /R U/R
Jeżeli obwód elektryczny jest zamknięty to punkty 1 i 2 pokrywają się, V1 = V2 i trzymujemy
prawo Ohma dla zamkniętego obwodu:
𝐈=
ℇ𝟏𝟐
𝐑
gdzie ℇ12 jest siłą elektromotoryczną działającą w obwodzie, a R jest całkowitym oporem
obwodu. W ogólnym przypadku R = r + R1, gdzie r – opór wewnętrzny źródła, a R1 – opór
zewnętrznej części. W związku z tym prawo Ohma dla danego obwodu będzie miało postad:
Piotr Posmykiewicz – Wykład z fizyki
16
ℇ
𝟏𝟐
𝐈 = 𝐑+𝐫
Jeżeli obwód jest rozwarty i co za tym idzie, nie płynie w nim prąd (I = 0), to z prawa
Ohma 2.21 otrzymujemy, że E12 = V1 – V2, tzn. SEM w otwartym obwodzie jest równa różnicy
potencjałów na jego koocach. W rezultacie, jeżeli chcemy znaleźd SEM źródła prądu, to
należy zmierzyd różnicę potencjałów na jego zaciskach.
17.7 Prawa Kirchhoffa dla rozgałęzionych obwodów.
Uogólnione prawo Ohma można z powodzeniem stosowad do dowolnie złożonego
obwodu z prądem. Jednak bezpośrednie rozwiązanie dla rozgałęzionego obwodu,
zawierającego kilka zamkniętych obwodów (oczek – oczka mogą mied wspólne części, a
każde oczko może zawierad kilka źródeł prądu) jest na ogół
I1
I5
dośd złożone. Obliczenia upraszczają się znacznie, jeżeli
Węzeł
zastosowad dwa prawa Kirchhoffa.
Dowolny punkt rozgałęzienia obwodu, w którym spotykają
I2
I4
I3
się co najmniej trzy przewodniki z prądem nazywamy węzłem.
Jeżeli prąd wpływa do węzła, to przyjmuje się, że jest dodatni,
Rysunek 17.14
jeżeli wypływa z węzła, to przyjmuje się, że jest ujemny.
Pierwsze prawo Kirchhoffa: algebraiczna suma prądów, spotykających się w węźle jest
równa zero:
𝐢 𝐈𝐢
=𝟎
17.27
Na przykład dla sytuacji z Rysunku 17.14 pierwsze prawo Kirchhoffa zapisuje się:
I1 – I2 + I3 – I4 – I5 = 0
Pierwsze prawo Kirchhoffa wynika bezpośrednio z zasady zachowania ładunku.
Drugie prawo Kirchhoffa otrzymuje się z uogólnienia prawa Ohma dla rozgałęzionych
obwodów. Rozważmy obwód składający się z trzech odcinków (Rysunek 17.14). Przyjmijmy,
że dodatni kierunek obchodzenia tego obwodu odbywa się zgodnie z kierunkiem wskazówek
zegara (przy czym wybór nasz jest całkowicie dowolny). Wszystkie prądy, których kierunek
zgadza się z kierunkiem obchodzenia obwodu przyjmujemy za dodatnie, a te które są
przeciwne – za ujemne. SEM źródeł prądu uważamy za dodatnie, jeżeli wytwarzają one prąd
Piotr Posmykiewicz – Wykład z fizyki
17
zgodny z kierunkiem obchodzenia obwodu. Stosując prawo Ohma do odcinków (2.20)
możemy zapisad:
I1R1 VA VB E1
I2 R 2 VB VC E 2
I3R 3 VC VA E3
Dodając stronami te wyrażenia otrzymujemy
I1R1 I 2 R2 I3 R3 E1 E2 E3
17.28
I1R1 I 2 R2 I 3 R3 E1 E2 E3 0
lub
Równanie 2.22 przedstawia drugie prawo Kirchhoffa: dla dowolnego oczka wybranego z
rozgałęzionego obwodu suma algebraiczna iloczynów natężeo prądów I i i oporów Ri na
danych odcinkach oczka plus suma algebraiczna SEM ℇ𝐊 występujących w tym oczku jest
zawsze równa zero:
𝐢 𝐈𝐢 𝐑 𝐢
+
𝐤 ℇ𝐤
=𝟎
17.29
Podczas obliczeo z zastosowaniem praw Kirchhoffa dla złożonego obwodu należy:
1. Wybrad dowolnie kierunki natężeo prądów: właściwy kierunek prądów określimy
następująco:, jeżeli po rozwiązaniu równao otrzymane natężenie będzie dodatnie
tzn., że przyjęty kierunek był prawidłowy, jeżeli otrzymana wartośd natężenia prądu
będzie ujemna oznacza to, że kierunek rzeczywisty jest przeciwny do przyjętego
2. Wybrad kierunek obchodzenia
B
obwodu; iloczyny IR przyjmujemy
za
dodatnie,
jeżeli
E1
wzrostu potencjału na oporniku
pokrywa
się
z
E2
kierunek
I1R1
R2
R1
I2R2
kierunkiem
obchodzenia i odwrotnie; SEM
będziemy uważad za dodatnie,
jeżeli działają one w kierunku
I1
I2
A
E3
R3
I3R3
I3
C
Rysunek 17.15
obchodzenia obwodu (wzrasta
potencjał) i odwrotnie.
3. Zapisad tyle równao, aby ich ilośd była równa ilości szukanych wielkości; każde
rozpatrywane oczko powinno zawierad chociaż jeden element, który nie wystąpił w
rozpatrywanych wcześniej oczkach.
Piotr Posmykiewicz – Wykład z fizyki
18
Znaleźd, korzystając z praw Kirchhoffa, nieznany opór R1 dla
obwodu – mostka Wheatstone’a. Po zapisaniu praw Kirchhoffa
założyd, że tak dobieramy opory, iż przez galwanometr nie płynie
prąd (Rysunek 17.16).
Rysunek 17.16
17.8 Klasyczna teoria metali.
Nośnikami ładunku w przewodnikach są swobodne elektrony. Istnienie swobodnych
elektronów w przewodniku można wyjaśnid w następujący sposób: Podczas tworzenia się
siatki krystalicznej metalu (w wyniku zbliżania oddzielnych atomów) elektrony walencyjne,
które są stosunkowo słabo związane z jądrami atomowymi, stają się swobodne i mogą
poruszad się po całej objętości kryształu. W rezultacie, w węzłach siatki krystalicznej znajdują
się jony, a między nimi poruszają się chaotycznie elektrony, posiadające według
elektronowej teorii metali własności takie jak gaz doskonały.
Swobodne elektrony podczas ruchu zderzają się z jonami w siatce krystalicznej i w
wyniku tego ustala się pewien stan równowagi cieplnej między elektronami, a siatką
krystaliczną. Zgodnie z teorią Drude’a - Lorenza elektrony posiadają taką samą energię ruchu
cieplnego jak cząsteczki gazu jednoatomowego. Dlatego stosując wnioski z teorii kinetycznomolekularnej
można
znaleźd
średnią
prędkośd
ruchu
cieplnego
elektronów
5
u sr 8kT/πm0 , która dla temperatury T = 300K wynosi u sr 1,08 10 m/s . Cieplny ruch
elektronów jest chaotyczny i nie może spowodowad powstania prądu.
Jeżeli przyłożyd zewnętrzne pole do metalowego przewodnika, to oprócz ruchu cieplnego
powstaje ruch uporządkowany tzn. przepływ prądu. W rezultacie prędkośd średnią <v>
można ocenid korzystając ze wzoru 17.3 J = nevd . Jeżeli za gęstośd prądu j podstawimy
maksymalną dopuszczalną gęstośd dla przewodów miedzianych - 107 A/m2 , to przy gęstości
elektronów n 8 1028 m3 otrzymamy, że średnia prędkośd uporządkowanego ruchu
4
elektronów wyniesie vd 7,8 10 m/s . Widad, zatem, że vd << usr, tzn., że nawet dla
bardzo dużych prądów średnia prędkośd uporządkowanego ruchu elektronów jest znacznie
mniejsza od ich prędkości ruchu cieplnego. Wydawałoby się, że otrzymany wynik przeczy
znanemu faktowi, iż prędkośd rozchodzenia się prądu elektrycznego jest olbrzymia - rzędu
prędkości rozchodzenia się światła a w próżni ( c 3 108 m/s ). Jest to tylko pozorna
Piotr Posmykiewicz – Wykład z fizyki
sprzecznośd,
ponieważ
19
prędkośd
c
jest
prędkością
rozprzestrzeniania
się
pola
elektromagnetycznego wzdłuż przewodów.
17.9 Wyprowadzenie podstawowych praw elektryczności z klasycznej teorii
metali.
1. Prawo Ohma. Niech w metalowym
przewodniku istnieje pole elektryczne o
stałym natężeniu E = const. Od strony pola
na elektron działa siła F = eE i uzyskuje on
przyspieszenie
rezultacie,
a
w
=F/m
czasie
=
eE/m.
W
swobodnego
przemieszczenia elektrony poruszają się z
jednakowym przyspieszeniem i na koocu tej
Średnie przemieszczenie
Typowy tor elektronu,
𝐸=0
(a)
drogi uzyskują prędkośd
Typowy tor elektronu,
𝐸≠0
(b)
Rysunek 17.17
vmax eEt sr /m
gdzie tsr - średni czas między dwoma kolejnymi zderzeniami elektronu z jonami siatki.
Zgodnie z teorią Drude’a, na koocu swobodnego przejścia, elektron zderzając się z jonem
siatki oddaje mu zgromadzoną w polu energię, w wyniku, czego jego prędkośd spada do zera.
W rezultacie średnia prędkośd ukierunkowanego ruchu elektronu (prędkośd dryfu) będzie
równa
vsr vd u max 0/2 eEt sr / 2m
17.30
Średni czas tśr swobodnego przebiegu będzie określony przez średnią długośd
swobodnego przebiegu lśr (Rysunek 17.17b) i przez średnią prędkośd ruchu elektronów
względem siatki krystalicznej uśr + vd (uśr - średnia prędkośd ruchu cieplnego elektronów). Z
poprzedniego paragrafu wiadomo, że vd << uśr, i dlatego
t sr lsr /u sr
Podstawiając wartośd to do 17.30 otrzymujemy:
vd eEl sr / 2mu sr
Gęstośd prądu w metalicznym przewodniku jest równa
J nev d
ne 2lsr
E
2mu sr
17.31
Piotr Posmykiewicz – Wykład z fizyki
20
Widad, że gęstośd prądu jest proporcjonalna do natężenia pola, tzn. otrzymaliśmy prawo
Ohma w postaci różniczkowej (wzór 17.3). Współczynnik proporcjonalności między J i E jest,
zatem przewodnością właściwą metalu
γ
ne 2lsr
,
2mu sr
17.32
która jest tym większa im większa jest gęstośd swobodnych elektronów i im większa średnia
długośd ich swobodnego przebiegu.
2. Prawo Joule’a – Lenza. Na koocu swobodnego przebiegu elektron uzyskuje dodatkową
energię kinetyczną:
Ek
mv 2max
e 2lsr2 2
E
2
2mu sr2
17.33
Podczas zderzenia elektronu z jonem energia ta przekazywana jest całkowicie siatce i idzie na
zwiększenie energii wewnętrznej metalu, tzn. jego nagrzanie.
W jednostce czasu elektron doznaje średnio z zderzeo z węzłami siatki
z u sr /l sr
17.34
Jeżeli n jest gęstością elektronów, to w jednostce czasu zajdzie nz zderzeo i siatce zostanie
przekazana energia
w nz E k
17.35
która idzie na nagrzanie przewodnika. Podstawiając2.25 i 2.26 do 2.27 otrzymujemy
w
ne 2lsr 2
E
2mu sr
17.36
gdzie w jest mocą właściwą prądu. Współczynnik proporcjonalności między w i E2 zgodnie z
17.32 jest przewodnictwem właściwym γ; w rezultacie wyrażenie 17.36 określa prawo
Joule’a - Lenza w postaci różniczkowej (patrz równanie 17.22).
4. Prawo Wiedemanna-Franza. Metale charakteryzują się zarówno dużym przewodnictwem
elektrycznym jak i wysokim przewodnictwem cieplnym. Wynika to z tego, iż nośnikami prądu
i ciepła są te same nośniki – swobodne elektrony.
Na drodze doświadczalnej Wiedemann i Franz podali prawo, zgodnie, z którym stosunek
przewodności cieplej (λ) i przewodności właściwej (γ) dla wszystkich metali w tej samej
temperaturze jest jednakowy i zwiększa się proporcjonalnie do temperatury bezwzględnej
λ/γ = βT
Piotr Posmykiewicz – Wykład z fizyki
21
gdzie β – stała nie zależna od rodzaju metalu.
Z klasycznej teorii metali, po uwzględnieniu rozkładu prędkości elektronów, wynika, że β
= 2(k/e2). Tymczasem dane doświadczalne pokazują, że β jest raczej równe 3(k/e2). Tak więc,
klasyczna teoria tylko jakościowo wyjaśnia prawo Wiedemanna – Franza. Oprócz tego teoria
klasyczna metali napotyka jeszcze inne trudności. Rozpatrzmy niektóre z nich.
Zależnośd oporu od temperatury. Ze wzoru (17.32) na przewodnośd właściwą metali
wynika, że opór metali tzn., wielkośd odwrotna do γ, powinna wzrastad proporcjonalnie do
T ( w 17.32 n i lśr nie zależą od temperatury, a uśr ~ T). Przeczy to jednak danym
doświadczalnym, które pokazują, że R~T.
Ocena średniej długości swobodnego przebiegu elektronów. Aby γ ze wzoru zgadzało
się zdanymi eksperymentalnymi należy przyjąd, że lśr jest znacznie większe od rzeczywistych,
innymi słowy, należy założyd, że elektron przebywa bez zderzeo z jonami siatki drogę setek
odległości międzywęzłowych. Takie założenie z kolei nie zgadza się z teorią Drude’a Lorenza.
Pojemnośd cieplna metali. Pojemnośd cieplna metalu składa się z pojemności cieplnej
jego siatki krystalicznej i pojemności cieplej gazu elektronowego. Dlatego też pojemnośd
cieplna przypadająca na jeden mol metalu powinna byd znacznie większa od takiej
pojemności dielektryka, które nie posiadają swobodnych elektronów. Zgodnie z prawem
Dulonga-Petit pojemnośd cieplna jednoatomowego kryształu wynosi 3R. Uwzględniając, że
chaotyczny ruch elektronów charakteryzuje się trzema stopniami swobody otrzymamy, że
pojemnośd cieplna gazu elektronowego wyniesie 3/2R. W rezultacie pojemnośd cieplna
jednego mola metalu powinna byd równa 4,5R. Jednak doświadczenie pokazuje, że wynosi
ona 3R tzn. zarówno dla metali jak i dielektryków spełnione jest prawo Dulonga - Petit. Tak,
więc obecnośd swobodnych elektronów nie ma wpływu na pojemnośd cieplną. Jest to
niezrozumiałe z punktu widzenia klasycznej teorii metali.
Otrzymane rozbieżności teorii z doświadczeniem można wyjaśnid tym, iż ruch elektronów
w metalach podlega nie prawom mechaniki klasycznej, a prawom mechaniki kwantowej, a
zatem zachowanie elektronów przewodzenia w metalu jest opisane nie przez statystykę
Maxwella – Boltzmanna, a przez statystykę kwantową. Zgodnie z wnioskami wynikającymi z
teorii kwantowej w przypadku idealnego kryształu, w którym wszystkie atomy znajdują się na
swoich miejscach, elektrony nie powinny doznawad w ogóle zderzeo z jonami. Jednak w
przypadku T > 0 atomy drgają wokół swoich położeo równowagi. Gdy temperatura wzrasta,
Piotr Posmykiewicz – Wykład z fizyki
22
wzrasta amplituda drgao i zderzenia stają się częstsze i średnia droga swobodna maleje. W
rezultacie opór wzrasta wraz z temperaturą.