Pasma energetyczne

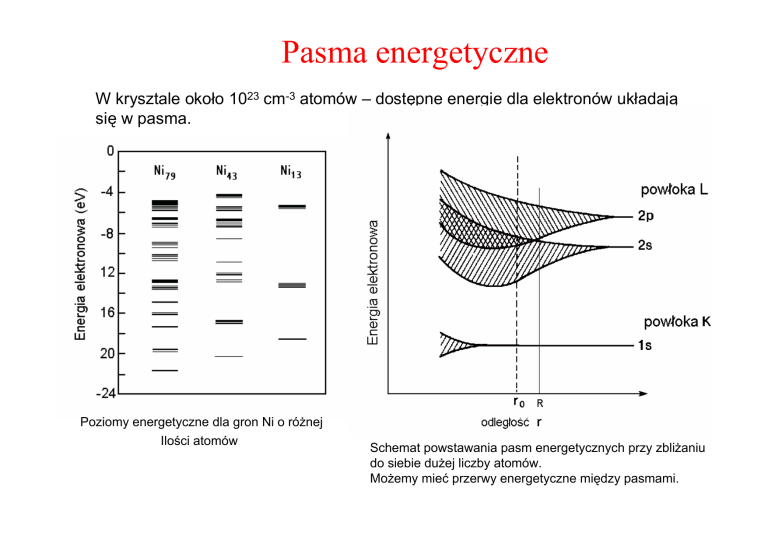
Pasma energetyczne
W krysztale około 1023 cm-3 atomów – dostępne energie dla elektronów układają
się w pasma.
Poziomy energetyczne dla gron Ni o różnej
Ilości atomów
Schemat powstawania pasm energetycznych przy zbliżaniu
do siebie dużej liczby atomów.
Możemy mieć przerwy energetyczne między pasmami.
Do opisu posługujemy się przybliżeniami.
- Elektrony traktujemy jako lekkie i dopasowujące się do chwilowego położenia rdzeni
w węzłach sieci krystalicznej – przybliżenie adiabatyczne, jak dla cząsteczek.
- Ponadto traktujemy elektrony jako niezależne cząstki, poruszające się w potencjale
periodycznym o okresie sieci krystalicznej – potencjał ten jest wypadkowym
potencjałem rdzeni atomowych i pozostałych elektronów walencyjnych. Jest to tzw.
przybliżenie jednoelektronowe.
Dla przypadku jednowymiarowego kryształu o stałej sieci a
Hamiltonian wygląda następująco:
⎡ h2 d 2
⎤
+ V ( x)⎥ψ ( x) = Hψ ( x) = Eψ ( x)
⎢−
2
⎣ 2m0 dx
⎦
Periodyczny potencjał spełnia warunek:
V ( x) = V ( x + a)
Rozwiązaniem Hamiltonianu są tzw. funkcje Blocha,
gdzie funkcja u k (x ) jest periodyczna z okresem sieci
W przypadku trójwymiarowym
ψ ( x) = e ikx ⋅ u k ( x )
rr
r
r
ik x
ψ (r ) = e ⋅ u k (r )
rr
r
r
ik x
ψ (r ) = e ⋅ u k (r )
funkcja Blocha
Zatem funkcje własne hamiltonianu są iloczynem fali płaskiej i funkcji o okresie sieci
krystalicznej
funkcja Blocha
Pasma energetyczne
Metale. Model elektronów prawie swobodnych.
- jądra + elektrony powłok zamkniętych → nierozdzielne jony – rdzenie atomowe
- elektrony walencyjne – stosunkowo słabo związane. W wyniku oddziaływań
odrywają się od macierzystych rdzeni i poruszają się niemal swobodnie w całej
objętości kryształu.
Kryształ związany dzięki elektrostatycznym oddziaływaniom pomiędzy ujemną
chmurą elektronową a dodatnimi jonami.
Własności:
a) duże przewodnictwo elektryczne
b) kowalność. Ponieważ jony metalu nie są ze sobą ściśle związane i mogą się
względem siebie stosunkowo łatwo przesuwać, niewielkimi siłami można zmienić
kształt.
Model elektronów prawie swobodnych.
Założenie:
Potencjał periodyczny oddziałujący na elektrony walencyjne jest słabym zaburzeniem,
czyli elektronowe funkcje falowe są w pierwszym przybliżeniu kombinacjami falr
płaskich. Energia w pierwszym przybliżeniu jest kwadratową funkcją wektora k
Poprawki do energii (od potencjału periodycznego) liczone w rachunku zaburzeń
dają przerwy energetyczne.
r
k
Przerwy energetyczne występują dla wektora
w pobliżu granicy tzw. strefy
Brillouina. Strefa Brillouina jest komórką elementarną sieci odwrotnej.
Wektory sieci odwrotnej zdefiniowane są następująco:
r r
g j ai = 2πδ ij
czyli
r r
2π (a2 × a3 )
r
g1 = r r r
a1 ⋅ (a 2 × a3 )
r r
r
2π (a × a )
g 2 = r r3 r1
a1 ⋅ (a2 × a3 )
r r
r
2π (a × a )
g 3 = r r1 r2
a1 ⋅ (a2 × a3 )
Dla sieci jednowymiarowej o stałej sieci a, wektor sieci odwrotnej
2π
g=
a
i granice strefy Brillouina występują dla
±
π
a
Ważny wniosek!
•
Z ogólnego warunku periodyczności wynika, że możliwe stany
elektronowe nie są ograniczone do pojedynczej paraboli w przestrzeni k,
lecz równie dobrze mogą być znalezione na parabolach przesuniętych o
r
dowolny wektor sieci odwrotnej G = n gr + n gr + n gr
1 1
•
2
2
3
3
W przypadku granicy strefy, tam gdzie przecinają się dwie parabole
rachunek zaburzeń dla zdegenerowanych stanów własnych.
Dalsze uproszczenia
(
)
V ( x) = −V e igx + e − igx = −2V cos( gx)
•
•
Rozważmy stan w pobliżu granicy strefy, k = g/2 – η = π/a – η
Możemy wówczas pominąć przyczynki od bardziej odległych stanów
energetycznych.
•
Pamiętamy, że
e
⎡⎛ g ⎞ ⎤
i ⎢⎜ ⎟− g ⎥ x
⎣⎝ 2 ⎠ ⎦
=e
Ψ ( x ) = c1e
g
−i x
2
⎛g
⎞
i ⎜ −η ⎟ x
⎝2 ⎠
+ c2 e
⎛ g
⎞
i ⎜ − −η ⎟ x
⎝ 2 ⎠
Po podstawieniu tej postaci funkcji falowej do hamiltonianu,
pomnożeniu przez funkcję sprzężoną i wycałkowaniu po obszarze
komórki elementarnej otrzymujemy:
2
⎡ h2 ⎛ g
⎤
⎞
⎜ − η ⎟ − E ⎥ c1 − Vc 2 = 0
⎢
⎠
⎥⎦
⎣⎢ 2 m 0 ⎝ 2
2
⎤
⎡ h2 ⎛ g
⎞
− Vc 1 + ⎢
⎜ + η ⎟ − E ⎥c 2= 0
⎠
⎢⎣ 2 m 0 ⎝ 2
⎥⎦
•
Dwa rozwiązania
1 ⎧⎪ h 2
E± = ⎨
2 ⎪⎩ 2m0
2
h2
⎞
⎛g
⎜ −η ⎟ +
⎠ 2 m0
⎝2
2
⎛g
⎞
⎜ +η ⎟ ±
⎝2
⎠
⎫
⎛ h ⎛g
⎞
h ⎛g
⎞ ⎟
⎞
2⎪
⎜
−
−
+
+
η
η
4
V
⎟ ⎟
⎟
⎜
⎬
⎜ 2 m0 ⎜⎝ 2
⎠ 2 m0 ⎝ 2
⎠ ⎠
⎪
⎝
⎭
2
2
2
2
2
Na granicy strefy pojawia się przerwa energetyczna,
η→0
1 ⎡ h2
E± = ⎢
2 ⎢⎣ 2 m0
1
2
⎛ h
⎜
⎜ 2 m0
⎝
2
2
h2
⎛g⎞
⎜ ⎟ +
⎝ 2 ⎠ 2 m0
2
2
h
⎛g⎞
⎜ ⎟ −
⎝ 2 ⎠ 2 m0
2
⎛g⎞
⎜ ⎟
⎝2⎠
⎛g⎞
⎜ ⎟
⎝2⎠
2
2
⎤
⎥±
⎥⎦
2
⎞
⎟ + 4V 2
⎟
⎠
2
h ⎛g⎞
E± =
⎜ ⎟ ±V
2m0 ⎝ 2 ⎠
Na granicy strefy pojawia się przerwa energetyczna, η→0
•
•
Ponieważ funkcja Blocha przesunięta o wektor sieci odwrotnej nie zmienia
się to wygodnie jest przedstawiać wyniki tylko w I-szej strefie Brillouina.
Trzeba wówczas numerować pasma energetyczne.
Stan elektronu w ciele stałym zadany jest przez wektor falowy z I-szej strefy,
numer pasma oraz rzut spinu.
Elektron w ciele stałym jako quasi-cząstka
• Zależność E(k) dla elektronu w ciele stałym różni się od
zależności dla elektronu swobodnego (próżni), ponieważ
elektron w krysztale stale oddziałuje z pozostałymi cząstkami
układu – elektronami i jądrami.
• Quasi – cząstka → elektron w ciele stałym.
r
• Wokół ekstremów zależności energii od wektora k możemy
zapisać zależność energii analogicznie jak dlar cząstki
swobodnej, w drugiej potędze tego wektora k
r r 2
h (k − k 0 )
E=
+ E0
2m *
2
m* jest masą efektywną
Kryształy kowalencyjne
• Podobnie jak dla metali→ rdzenie atomowe +
elektrony walencyjne.
• Inaczej niż dla metali → elektrony walencyjne są
zlokalizowane.
Metoda ciasnego wiązania
(zmodyfikowana metoda orbitali molekularnych)
2
h
r r
r r
Hˆ = Hˆ A + V = −
∇ 2 + V A ( r − rn ) + v ( r − rn )
2m
•
VA – potencjał swobodnego atomu
r r
r r
v(r − rn ) = ∑V A (r − rm )
m≠ n
r
Ψk Hˆ Ψk
E (k ) =
Ψk Ψk
r
Φ k Hˆ Φ k
E (k ) ≤
Φk Φk
Metoda ciasnego wiązania
•
•
Stany energetyczne E(k) elektronu w krysztale, wywodzące się z poziomu
energetycznego Ei swobodnego atomu.
Zakładamy, że funkcja falowa jest kombinacją liniową atomowych funkcji
własnych
rr
r r
r r
ik rn
Φ k = ∑ a n Φ A ( r − rn ) = ∑ e Φ A ( r − rn )
n
n
Φk Φk = ∑ e
r r r
ik ( rn − rm )
n,m
r r
r r r
*
Φ
A ( r − rm )Φ A ( r − rn ) dr
∫
Dla elektronu zlokalizowanego funkcja ΦA ma znaczące wartości tylko w sąsiedztwie
węzła sieci rm. Dlatego uwzględniamy tylko wyrażenia dla których m=n
N – liczba atomów w krysztale.
r r
r r r
Φ k Φ k ≈ ∑ ∫ Φ* A (r − rn )Φ A (r − rn )dr = N
n
Metoda ciasnego wiązania
r
1
E (k ) ≈
N
∑e
n ,m
r r r
ik ( rn − rm )
[
]
r r
r r
r r r
∫ Φ A (r − rm ) Ei + v(r − rn ) Φ A (r − rn )dr
*
• Dla wyrazów zawierających zaburzenie v(r-rn) uwzględniamy
przekrywanie funkcji falowych zlokalizowanych na
najbliższych sąsiadach.
r r
r r
r r r
Ai = − ∫ Φ *i ( r − rn )v ( r − rn ) Φ i ( r − rn ) d r
r r
r r
r r r
B i = − ∫ Φ *i ( r − rm )v ( r − rn ) Φ i ( r − rn ) d r
r r r
r
i k ( rn − rm )
E ( k ) ≈ E i − Ai − B i ∑ e
m
Suma po m zawiera tylko te wartości, dla których rm opisuje
najbliższych sąsiadów rn. Ai > 0
Sieć regularna prosta
r r
rn − rm = (±a,0,0); (0,±a,0); (0,0,±a)
r
E (k ) ≈ Ei − Ai − 2Bi (cos(k x a) + cos(k y a) + cos(k z a))
Uwagi!
• w pobliżu k = 0
r
E ( k ) ≈ Ei − Ai − 6 Bi + Bi a 2 k 2
Szerokość pasma tym większa im większe Bi
(przekrywanie się funkcji falowych
sąsiadujących atomów).
W. Ibach
Przykłady
J. Ginter
W. Ibach
Przykłady
Przewodniki i izolatory
Izolator, półprzewodnik:
- elektrony walencyjne całkowicie wypełniają jedno lub więcej pasm,
- liczba elektronów walencyjnych w prostej komórce w krysztale jest parzysta
Metale:
- jeden elektron walencyjny przypadający na jedną prostą komórkę – pasmo
zapełnione w połowie lub
- parzysta liczba elektronów i zachodzenie na siebie pasm.
Ekscytony
Rx
μ 1 Ry
=− 2
E ( n) = −
2
2
m0 ε n
n
rn =
m0
μ
εn 2 a B = n 2 a x
Para elektron-dziura związana kulombowsko.
Energia wiązania jest energią kulombowską,
znacznie mniejszą niż dla atomu wodoru.
Rx
En = E g − 2
n
Półprzewodniki domieszkowe
Płytkie domieszki
•
Odbicie plazmowe
M. Fox
Głębokie domieszki – poziomy energetyczne w
obszarze przerwy energetycznej
Al2O3 domieszkowany Cr – absorpcja związana ze wzbudzeniem Cr
odpowiedzialna za czerwony kolor rubinu
Doświadczalne metody wyznaczania przerw
energetycznych
M. Fox
Absorpcja domieszkowa i fononowa
w obszarze podczerwieni
Odbicie od plazmy elektronowej
Absorpcja w obszarze przerwy energetycznej
- malenie transmisji
Obsadzenie stanów
• Rozkład Fermiego-Diraca
f 0=
1
E − EF
1+ e
k0 T
Prawdopodobieństwo obsadzenia
stanu kwantowego o energii E
EF – potencjał chemiczny
EF =
∂F
∂ni
F = U − TS
Półprzewodnik samoistny
Koncentracja (gęstość) elektronów o
energii z przedziału (E, E + dE)
dn = f 0 ( E , T ) g e ( E ) dE
ge =
1 ⎛ 2m
⎜
2 π 2 ⎜⎝ h 2
*
e
⎞
⎟⎟
⎠
3
2
E − Ec
1
f 0=
E − EF
1+ e
k0 T
Zakładamy, że EF jest w przerwie
energetycznej, (E – EF) >> k0T
f0 ≈ e
−
(E −EF )
k 0T
Półprzewodnik samoistny
• Prawdopodobieństwo znalezienia dziury w paśmie
walencyjnym
1
fh = 1− f0 =
1+ e
−( E − E F )
k0T
1 ⎛ 2m
⎜ 2
g h (E ) =
2 ⎜
2π ⎝ h
*
h
≈e
⎞
⎟⎟
⎠
3
2
( E − EF )
k0T
Ev − E
Koncentracja elektronów i
dziur
∞
1 ⎛ 2me* ⎞
⎜ 2 ⎟⎟
n = ∫ f 0 g e dE =
2 ⎜
2π ⎝ h ⎠
Ec
3
2
⎛m k T ⎞
⎟⎟ e
n = 2⎜⎜
⎝ 2πh ⎠
*
e 0
2
p=
3
2 ∞
E F − Ec
k0T
∫e
−
( E − EF )
k 0T
Ec
E F − Ec
= Nce
k0T
Ev
∫f
h
g h dE
−∞
3
2
⎛m k T ⎞
⎟⎟ e
p = 2⎜⎜
⎝ 2πh ⎠
*
h 0
2
−
( E F − Ev )
k0 T
= Nve
−
( E F − Ev )
k0 T
E − Ec dE
Półprzewodnik samoistny
• n=p
• Eg = E c - Ev
3
3
* 2
h
⎛ kT ⎞
n ⋅ p = n 2 = 4⎜ 0 2 ⎟ (me* m ) e
⎝ 2πh ⎠
3
2
3
* 4
h
⎛ kT ⎞
n = p = 2⎜ 0 2 ⎟ (me* m ) e
⎝ 2πh ⎠
Nc
=e
Nv
( 2 EF − E g )
k0T
−
−
Eg
k0T
Eg
2 k0T
⎛ mh* ⎞
1
3
⇒ EF = Eg + k0T ln⎜⎜ * ⎟⎟
2
4
⎝ mh ⎠
Półprzewodnik samoistny
J. Singleton
Półprzewodniki domieszkowe
• Tzw. „płytkie domieszki”
• np. P w Si
Donory
np. In w Si
Akceptory
Model wodoropodobny
• Piąty elektron porusza się w polu wytworzonym przez
centrum fosforu oraz pozostałe atomy. Centrum P ma
ładunek +1e, wytwarza dodatkowy potencjał
kulombowski.
Model wodoropodobny
• Ostatecznie zagadnienie sprowadza się
do problemu atomu wodoru z nośnikiem
swobodnym o masie m*, w ośrodku
dielektrycznym ze stałą ε i małą
„poprawką” do potencjału.
⎛ m* ⎞ 13.6eV
En = −⎜⎜ ⎟⎟ 2 2
⎝ m0 ⎠ ε n
J. Singleton
Donory i akceptory
Własności elektryczne
−
A
+
D
n+ N = N + p
• Wysoka temperatura: n = ND - NA
• Niskie temperatury
n∝e
−
ED
2 k0T
⎛ ND ⎞
1
1
⎟⎟
EF = (Ec + ED ) + k0T ln⎜⎜
2
2
⎝ Nc ⎠
Własności elektryczne
J. Singleton
Przewodnictwo
Przewodnictwo
r
j = −envD = neμE = σE
σ = neμ
Ruchliwość
μ=
Dwa rodzaje nośników
eτ
m
σ = neμ e + peμ p
Zależność oporu od
temperatury
Metal
Półprzewodnik