Prądy indukcyjne

Prądy indukcyjne.
Sposoby wzbudzania prądów indukcyjnych.
Warunkiem wzbudzenia prądu w obwodzie jest przepływanie przez ten obwód zmiennego strumienia magnetycznego.
Miarą strumienia indukcji magnetycznej jest iloczyn indukcji magnetycznej pola, które w danym miejscu można uznać
za jednorodne, i elementu powierzchni prostopadłej do linii pola, przez którą dany strumień przepływa.
Aby uzyskać zmianę strumienia przepływającego przez dany obwód, trzeba spowodować zmianę indukcji
magnetycznej lub zmianę pola powierzchni obwodów, przez który strumień przepływa. Kierunek prądu indukcyjnego
określamy za pomocą reguły Lenza (zwanej też regułą przekory), która jest szczególnym przypadkiem prawa
zachowania energii:
Kierunek prądu indukcyjnego jest taki, że wywołany przez ten prąd strumień
strumienia, które spowodowały powstanie tego prądu indukcyjnego.
przeciwdziała zmianom
Wymienimy kilka możliwych sposobów wywoływania prądów indukowanych w obwodach zamkniętych (cewce z
galwanometrem), czyli, innymi słowy, kilka sposobów wywoływania zmiennego w czasie strumienia magnetycznego
Φ, przechodzącego przez powierzchnię objętą konturem obwodu
1) ruch magnesu względem obwodu lub odwrotnie, gdyż istotne znaczenie ma tutaj ruch
względny magnesu i obwodu, pociągający za sobą zmianę opisanego wyżej strumienia
magnetycznego,
2) ruch obwodu z prądem względem drugiego obwodu zamkniętego lub zmianę
natężenia prądu w obwodzie I, uzyskaną ruchem suwaka.
INDUKCJA ELEKTROMAGNETYCZNA I PRAWA MAXWELLA.
W 1831 roku Faraday zauważył że, jeżeli przez powierzchnię ograniczoną zamkniętym liniowym obwodem
elektrycznym (przewodnikiem) przenika zmienny w czasie strumień wektora indukcji magnetycznej, to w tym
obwodzie płynie prąd, który nazywamy indukcyjnym.
Jak wiemy, aby w przewodniku mógł płynąć prąd należy przyłączyć go do źródła siły elektromotorycznej, które
wytworzy w przewodniku pole elektryczne i dostarczy energii potrzebnej do utrzymania uporządkowanego ruchu
ładunków elektrycznych. Źródłem energii potrzebnej do powstania i podtrzymania przepływu prądu indukcyjnego jest
praca wykonywana przy zmianie strumienia magnetycznego przenikającego przez powierzchnię ograniczoną danym
obwodem elektrycznym. Wartość siły elektromotorycznej indukcji powstającej w danym obwodzie jest równa
szybkości zmiany strumienia magnetycznego przenikającego przez powierzchnię danego obwodu.
E1  = 1 Wb/1 m
Ei 
d B
dt
2
= 1V
Jeżeli strumień magnetyczny zależy wprost proporcjonalnie od czasu, to wartość siły elektromotorycznej indukcji
równa się:
Ei 
 B
t
Kierunek prądu indukcyjnego określa reguła Lenza zwana też regułą przekory - prąd indukcyjny ma taki kierunek,
aby wytworzone przez niego pole magnetyczne przeciwdziałało zmianom strumienia magnetycznego które,
spowodowały powstanie tego prądu.
Jeżeli przyczyną powstania prądu indukcyjnego jest wzrost strumienia magnetycznego przez powierzchnię danego
obwodu, to wektor indukcji magnetycznej pola magnetycznego prądu indukcyjnego odejmuje się od wektora indukcji
magnetycznej pola zewnętrznego.
Jeżeli przyczyną powstania prądu indukcyjnego jest zmniejszanie się strumienia magnetycznego przez powierzchnię
danego obwodu, to wektor indukcji magnetycznej pola magnetycznego prądu indukcyjnego dodaje się do wektora
indukcji magnetycznej pola zewnętrznego.
Reguła Lenza wynika bezpośrednio z zasady zachowania energii. Gdyby pole magnetyczne prądu indukcyjnego
zwiększało zmiany strumienia magnetycznego przez powierzchnię danego obwodu, to dzięki dodatniemu sprzężeniu
zwrotnemu uzyskalibyśmy nieograniczone źródło energii elektrycznej, której wytwarzanie nie wymagałoby
dostarczenia energii z zewnątrz.
Regułę Lenza (a dokładniej zasadę zachowania energii) uwzględniamy w prawie indukcji elektromagnetycznej
Faradaya dopisując znak minus przed szybkością zmiany strumienia magnetycznego.
Ei  
d B
dt
Strumień wektora indukcji magnetycznej przez daną powierzchnię jest zdefiniowany jako
 
ΦB = B · S = B·S·cosα =
B  ·S = B· S 
gdzie B  - rzut B na kierunek prostopadły do danej powierzchni, a
prostopadłą do B .
S  rzut danej powierzchni na płaszczyznę
Jak wynika z powyższego wzoru powstanie siły elektromotorycznej indukcji w danym obwodzie elektrycznym możemy
spowodować na przykład:
a) zmieniając indukcję magnetyczną pola magnetycznego przechodzącego przez powierzchnię ograniczoną przez dany
obwód elektryczny,
b) zmieniając powierzchnię ograniczoną obwodem elektrycznym w danym polu magnetycznym
c) zmieniając kąt pomiędzy wektorem indukcji pola magnetycznego, a wektorem powierzchni ograniczonej obwodem
elektrycznym.
Rozpatrzmy kilka przykładów.
l. Przez powierzchnię obwodu w kształcie okręgu przechodzi pole magnetyczne, którego
linie sił są prostopadłe do płaszczyzny przewodnika (rysunek obok). Jeżeli indukcja
magnetyczna pola zewnętrznego jest zwrócona za płaszczyznę kartki, a jej wartość rośnie
proporcjonalnie do czasu Bz = kt, to w tym obwodzie powstanie siła elektromotoryczna
indukcji o stałej wartości Ei = –
d B
dB
=–
·S = – kS = –kr2 =const
dt
dt
a prąd indukcyjny popłynie przeciwnie do kierunku ruchu wskazówek
zegara tak, aby pole magnetyczne prądu indukcyjnego Bind
odejmowało się od pola zewnętrznego Bz przeciwdziałając wzrostowi
strumienia magnetycznego przez powierzchnię danego obwodu.
Zależności ΦB i Ei od czasu w powyższym przykładzie przedstawia
rysunek.
2. Rozpatrzmy solenoid (zwojnicę) przez którą płynie prąd o zmieniającym się natężeniu
W długim solenoidzie, przez który płynie prąd elektryczny powstaje
(rys.)
pole magnetyczne o
B = μo·
nI
l
gdzie
μo - przenikalność magnetyczna próżni,
n - liczba zwojów
l - długość solenoidu
I - natężenie prądu płynącego przez cewkę (zwojnicę)
Jeżeli natężenie prądu zmienia się, to zmienia się również indukcja magnetyczna w solenoidzie, a przez powierzchnie
zwojów solenoidu przechodzi zmienny w czasie strumień magnetyczny
ΦB = B·S = μo
nI
l
gdzie S jest polem powierzchni zwoju.
Należy pamiętać, że zmienne pole magnetyczne przenika przez powierzchnie wszystkich zwojów solenoidu. Powoduje
to powstanie w każdym zwoju siły elektromotorycznej indukcji własnej. Dla solenoidu o n zwojach wyindukowana siła
elektromotoryczna samoindukcji wynosi:
d B
 n 2 S dI
d  nI 
Es = - n
=-n
S   o
 o
dt
dt 
l 
l
dt
gdzie
on 2 S
l
=L
nosi nazwę współczynnika samoindukcji lub indukcji własnej obwodu, a siłę elektromotoryczną indukcji własnej
zapisujemy Es = - L
dI
dt
Jednostką współczynnika indukcji własnej jest henr
L  1V 1s  1H
1A
Jeżeli natężenie prądu w obwodzie z powyższego rysunku rośnie, to prąd indukcyjny popłynie w przeciwnym kierunku
niż prąd wytworzony przez ogniwo, jeżeli maleje, to prąd indukcyjny popłynie w tym samym kierunku co prąd
wytworzony przez baterię.
Wypełnienie solenoidu substancją ferromagnetyczną zwiększy jego współczynnik samoindukcji ale znacznie utrudni
jego obliczenie ponieważ jak wiemy μr dla ferromagnetyków zależy od tego czy i jak ferromagnetyk był
namagnesowany oraz od natężenia pola magnetycznego. Czyli μ r będzie zależeć od natężenia płynącego przez solenoid
prądu i kierunku jego przepływu.
3. Jeżeli mamy dwa obwody elektryczne ustawione tak (patrz
rysunek), że zmiana natężenia prądu w obwodzie pierwszym
spowoduje zmianę strumienia magnetycznego obejmowanego
przez obwód drugi, to powstająca w nim siła elektromotoryczna
będzie proporcjonalna do szybkości zmiany natężenia prądu w
obwodzie pierwszym
E i 2   
d B 2 1
dt
 M 2 1
dI 1
gdzie M2/1 - oznacza
dt
współczynnik indukcji wzajemnej obwodów 1 i 2, który tak jak współczynnik samoindukcji wyrażamy w henrach.
4. Rozpatrzmy ramkę z przewodnika umieszczoną w polu magnetycznym (o indukcji magnetycznej B )prostopadłym do
płaszczyzny ramki. Jeden z boków ramki może przesuwać się po dwóch bokach prostopadłych do niego
(rysunek).Przesunięcie boku ramki o odległość x spowoduje wzrost powierzchni obwodu elektrycznego o
S = l·x . Ponieważ ramka znajduje się w polu magnetycznym w obwodzie powstanie siła elektromotoryczna indukcji,
której wartość chwilowa wynosi
Ei = -
d B
dS
d
dx
 B
  B lx    Bl
  Blv
dt
dt
dt
dt
gdzie v- chwilowa wartość prędkości ruchu boku ramki
Jeżeli bok ramki będzie poruszał się ruchem jednostajnym, to w
ramce wyindukuje się stała siła elektromotoryczna. Ponieważ
strumień magnetyczny przez powierzchnię ramki rośnie, to prąd
indukcyjny popłynie przeciwnie do kierunku ruchu wskazówek
zegara.
5. Rozpatrzmy obwód elektryczny w kształcie ramki o powierzchni S który obraca się w jednorodnym polu
magnetycznym o indukcji B ruchem jednostajnym z prędkością kątową w (rysunek
obok) przy czym oś obrotu jest prostopadła do B . Jeżeli w chwili początkowej wektor
powierzchni jest równoległy do wektora indukcji pola magnetycznego, to strumień
magnetyczny przenikający przez powierzchnię ramki możemy zapisać:
ΦB = B·S·cosα = B·S·cos ωt
a siłę elektromotoryczną indukcji powstającą w ramce obliczamy zgodnie ze wzorem
Ei = -
d B
d
  B  S (cos ωt) = - B·S·ω·(-sin ωt) = B·S·ω·sin ωt = Eo sin ωt
dt
dt
gdzie Eo =BSω jest amplitudą czyli wartością maksymalną indukowanej siły elektromotorycznej sinusoidalnie
zmiennej (rysunek poniżej).
Powyższy przykład ilustruje zasadę działania technicznych źródeł energii elektrycznej (od prądnicy w rowerze do
elektrowni).
Foucalt wykazał, że prądy indukcyjne mogą powstawać nie tylko w zamkniętych obwodach liniowych, ale także w
przewodnikach masowych nieferromagnetycznych (np. płyta lub bryła metalu albo naczynie z elektrolitem). Jeżeli
przez przewodnik masowy przechodzi zmienny w czasie strumień magnetyczny, to w przekrojach tego przewodnika
prostopadłych do linii sił pola magnetycznego powstają prądy zwane wirowymi lub prądami Foucaulta o kierunku
określonym zgodnie z regułą Lenza. Prądy wirowe wykorzystywane są między innymi w piecach indukcyjnych do
wytapiania metali.
Analizując różne przypadki powstawania prądu indukcyjnego można zauważyć, że
1 ° ruch magnesu względem przewodnika kołowego powoduje wzbudzenie w nim Ei w wyniku
czego w przewodniku płynie prąd indukcyjny
2° ruch przewodnika kołowego względem nieruchomego magnesu też wzbudza E i w przewodniku
Uwaga: Wzbudzanie prądu indukcyjnego w przypadku 1° tłumaczymy wytworzeniem przez zmienne pole
magnetyczne zmiennego (wirowego) pola elektrycznego, które swym zasięgiem obejmuje przewodnik kołowy.
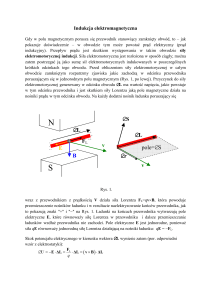
Przypadek 2° wyjaśniamy działaniem siły Lorentza na elektrony w przewodniku poruszające się z prędkością v razem z
całym przewodnikiem.
Powstawanie prądu indukcyjnego w nieruchomym przewodniku w wyniku zmian w czasie wektora indukcji
magnetycznej wymaga przyjęcia założenia zwanego drugim prawem Maxwella.
Zmienne w czasie pole magnetyczne wytwarza wirowe (także najczęściej zmienne) pole elektryczne, którego linie
sił mają kształt okręgów leżących w płaszczyźnie prostopadłej do linii sił zmiennego pola magnetycznego.
Stwierdzenie odwrotne nazywamy pierwszym prawem Maxwella.
Zmienne w czasie pole elektryczne wytwarza wirowe (także najczęściej zmienne) pole magnetyczne.
Trzecie prawo Maxwella mówi, że strumień wektora natężenia pola elektrycznego przez dowolną powierzchnię
zamkniętą równa się całkowitemu ładunkowi zawartemu wewnątrz tej powierzchni podzielonemu przez stałą
dielektryczną ośrodka ograniczonego tą powierzchnią.
Czwarte prawo Maxwella mówi, że strumień wektora indukcji magnetycznej przez dowolną powierzchnię
zamkniętą równa się zero.
 n

Niżej podaję bez wyprowadzenia matematyczny zapis praw Maxwella.
  n 
d E

I. K L B    Bi  l i    o I   o  o
dt
 i 1
L
n



d B
II. K L E   E i  l i
 E ind  
dt
i 1
L




III.
IV.
 E SZ
 B SZ = 0
  Qi
  i 1
 o


KL – oznacza krążenie wektora wzdłuż krzywej zamkniętej L a (Φ B)sz – oznacza strumień wektora przez
powierzchnię zamkniętą sz.




 SZ