Wykład 3

Wykład 3
Wymiana ciepła
1. Wprowadzenie
Proces wymiany ciepła jest procesem fizycznym związanym z
rozprzestrzenianiem się energii cieplnej. Można wyróżnić trzy sposoby,
przy pomocy których ciepło może być wymieniane
a) przewodzenie i przenikanie – kondukcja,
b) unoszenie lub przejmowanie – konwekcja,
c) promieniowanie – radiacja.
Podczas rozwiązywania zagadnień wymiany ciepła najczęściej stosujemy prawo
addytywności, które zakłada niezależność ww. rodzajów wymiany ciepła.
Oznacza to, że obliczone ilości energii cieplnej związanych z przewodzeniem,
unoszeniem i promieniowaniem niezależnie się sumuje. Podczas pożaru
występują wszystkie trzy typy wymiany ciepła, jednak w poszczególnych fazach
rozwoju pożaru, dominuje zazwyczaj jeden rodzaj wymiany ciepła np.
unoszenie spełnia szczególną rolę na początku pożaru, kiedy poziom
promieniowania cieplnego nie jest wysoki, promieniowanie stanowi
podstawową formę rozprzestrzeniania się ciepła, jeżeli średnica pożaru
przekracza 0,3 m. Mechanizm ten ma decydujący wpływ na rozwój pożaru w
pomieszczeniach.
Wpływ promieniowania cieplnego płomieni lub dowolnego ogrzanego obiektu
na pobliskie powierzchnie, może być oceniony tylko przy pomocy dokładnej
analizy procesów wymiany ciepła. Jest ona niezbędna do oceny czasu
ogrzewania materiałów palnych, do stanu przy którym następuje ich zapalenie.
2. Podstawowe pojęcia
Pole temperatur – zbiór temperatur w poszczególnych punktach rozpatrywanej
przestrzeni.
Ustalona wymiana ciepła – pole temperatur nie zmienia się w czasie.
Nieustalona wymiana ciepła – pole temperatur zmienia się w czasie np.
podczas pożarów, ogrzewania lub chłodzenia
stalowych elementów (hartowanie)
W większości procesów po pewnym okresie nieustalonej wymiany ciepła
układ dąży do stanu równowagi cieplnej, który charakteryzuje się stałym
rozkładem temperatur (
dT
 0 ).
d
Powierzchnia izotermiczna – zbiór punktów o jednakowych temperaturach.
Strumień ciepła (natężenie przepływu ciepła lub moc ciepła):
1

Q
dQ
d
[J/s]
Q

[J/s]
(2)
[W/m2]
(3)
(1)
Strumień ciepła dla przypadku ustalonego (stosunek ciepła Q do czasu  trwania
wymiany tej ilości ciepła):

Q
Gęstość strumienia ciepła:
q
d 2Q
dA d 
Gęstość strumienia ciepła dla przypadku ustalonego (stosunek strumienia ciepła

Q do pola A powierzchni izotermicznej, przez którą przepływa ten strumień):

a) powierzchniowa
Q
Q
qA  q  
A A
b) objętościowa
Q
qV 
V
c) liniowa
Q
qL 
L

[W/m2]
(4)
[W/m3]
(5)
[W/m]
(6)


Gęstość strumienia ciepła jest wektorem skierowanym prostopadle do
powierzchni izotermicznej w kierunku spadku temperatury.
3. Wprowadzenie do przewodnictwa ciepła
Rozprzestrzenianie się energii cieplnej wewnątrz ciała na drodze
wymiany energii cieplnej bezpośrednio pomiędzy sąsiednimi cząstkami oraz
dyfuzji drobin, atomów i swobodnych elektronów.
Wszystkie rozważania dotyczące przewodnictwa cieplnego są przeprowadzane
przy następujących założeniach:
1. Charakterystyki wszystkich procesów w danej objętości ciała są
funkcjami ciągłymi, również w czasie.
2. Straty energii na deformację termiczną w ciele są bardzo małe w porównaniu
ze zmianą energii wewnętrznej, tzn. proces zachodzi przy V=const.
3. Nie występuje w ciele konwekcja i promieniowanie cieplne.
Doświadczenia wykazują, że przy pomocy pierwszej i drugiej zasady
termodynamiki trudno jest matematycznie opisać procesy przewodnictwa.
W tym celu korzystamy z prawa podanego po raz pierwszy przez Bio
i Fouriera, które brzmi następująco:
„Wektor gęstości strumienia ciepła w przewodnictwie danego punktu
ciała równomiernie nagrzanego, w danym momencie czasu – jest wprost
proporcjonalny do wektora gradientu temperatury”
2
W postaci matematycznej prawo to można zapisać w następującej postaci:


q  - grad T
[W/m2]
(5)
T  T  T 
i
j
k
gdzie: grad T 
x
y
z

Współczynnik proporcjonalności  w W/mK zwany współczynnikiem
przewodnictwa zależy od temperatury i jest podawany w literaturze dla
określonego zakresu temperatur względnie ściśle określonej temperatury.
Wartość współczynnika przewodnictwa  waha się w granicach:
- dla gazów od 510-3 do 0,5 W/mK i wzrasta z temperaturą (od ciśnienia
praktycznie nie zależy w zakresie 0,3 do 2000 bar),
- dla cieczy od 810-3 do 0,6 W/mK i z reguły zmniejsza się ze wzrostem
temperatury (nie zależy od ciśnienia),
- dla metali od 7 do 360 W/mK i powoli zmniejsza się ze wzrostem temperatury
Zwykle przyjmuje się liniową zależność współczynnika przewodnictwa
cieplnego od temperatury w postaci:  = a + b T, gdzie a i b – stałe
właściwe dla danego materiału. W niskich temperaturach należy w tej
zależności uwzględnić człon nieliniowy, dodając wyrażenie c T2.
W tablicach są podawane wartości współczynnika dla różnych materiałów
i mediów. Występujące różnice wartości  wynikają często z trudnych do
określenia własności materiałów szczególnie budowlanych. Nawilżenie, róznice
w składzie chemicznym, czy gęstości, zmieniają zasadniczo przewodność
cieplną materiału i dlatego w przypadku braku danych zaleca się wyznaczać
wartość  przy pomocy pomiarów.
Równanie Bio-Fouriera nie uwzględnia skończonej prędkości przewodzenia
ciepła tzn. prędkości rozprzestrzeniania się ciepła w ciele, którą przyjęto za
nieskończoną. W przypadku analizowania procesów krótkotrwałych, należy
uwzględnić skończoną szybkość przewodzenia ciepła przez dodanie jednego
członu w równaniu Bio-Fouriera tzn.

q
q  - grad T -  r



(6)
gdzie: r – czas relaksacji (opóźnienia)
3
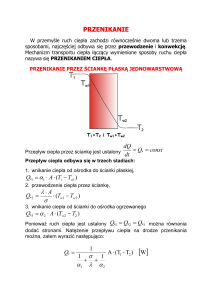
4. Ustalone przewodzenie i przenikanie ciepła przez ściankę płaską
W celu rozważenia przypadku ustalonego przenikania ciepła przez
ściankę płaską przyjęto następujące założenia:
1. Ściana płaska posiada grubość  znacznie mniejszą od wymiarów pola
jej powierzchni A.
2. Ściana jest wykonana z materiału o współczynniku przewodzenia ciepła .
3. Temperatura powierzchni ścianki z lewej strony (rys.) równa Ts1 jest wyższa
od temperatury powierzchni ścianki z prawej strony Ts2, czyli Ts1>Ts2 .
4. Temperatura ośrodka z lewej strony ścianki równa jest T1, zaś z prawej
strony ścianki T2.
5. Powierzchnie izotermiczne są równoległe do powierzchni ścianki.
Rys.1. Ścianka pojedyncza o grubości 
i współczynniku przewodzenia 
Rys.2. Ścianka podwójna o grubościach
1 i 2 i współczynnikach przewodzenia
2<1.
Gęstość strumienia ciepła przewodzonego przez
jednowarstwową
przy =const (szczególna postać równania Bio-Fouriera):
q

Ts1 - Ts2    1 T1 - Ts1    2 Ts2 - T2 

ściankę
[W/m2]
płaską
(7)
gdzie: 1 i 2 – współczynnik przejmowania i oddawania ciepła
[W/m2K]
4
Jeżeli współczynnik przewodzenia ciepła zależy liniowo od temperatury
[=0(1+bT)], to do równania (7) należy wstawić w miejsce stałej wartość
średniej arytmetycznej współczynników przewodzenia ciepła dla temperatur
powierzchni i ścianki.
Rozkład temperatury w ściance przy =const wyraża się wzorem:
T(x)  Ts1 -
Ts1 - Ts2
x

(8)
natomiast przy  zależnym liniowo od temperatury:
2
1  2qx 1

T(x)   Ts1   b   0b b

(9)
gdzie: x – współrzędna mierzona prostopadle do ścianki począwszy od
powierzchni 1.
Jeżeli b>0 to wypukłość krzywej jest skierowana do góry, jeżeli b<0, to
wypukłość krzywej jest skierowana do dołu.
Po dodaniu trzech równań (7) stronami otrzymamy:
 1 
1 

T1 - T2  q  



 1
2 
Stąd:
q   z T1 - T2 
(10)
(11)
1
1 
1 - współczynnik przenikania ciepła w J/m2hK
gdzie:
 
1  2
Opór przewodzenia ciepła ścianki płaskiej wielowarstwowej (rys.2) składającej
się z n warstw różnych materiałów prostopadłych do strumienia ciepła o
grubościach i oraz współczynnikach przewodzenia i jest sumą oporów
przewodzenia ciepła poszczególnych warstw.
W takim przypadku do wzoru (11) należy wstawić następujące wyrażenie na z:
z 
z 
1
1

n
1

1
r
 i 
 1 i 1 i  2
(12)
gdzie: r – opór przewodzenia ciepła
5
5. Ustalone przewodzenie i przenikanie ciepła przez ściankę walcową
W praktyce technicznej mamy do czynienia najczęściej ze ściankami
krzywymi np. rurami, które posiadają kształt walca.
W celu rozważenia przypadku ustalonego przenikania ciepła przez ściankę
walcową przyjęto następujące założenia:
1. Ścianka walcowa posiada długość l, która jest znacznie większa od średnicy.
2. Wewnętrzna powierzchnia o promieniu rw posiada temperaturę Tsw.
3. Zewnętrzna powierzchnia o promieniu rz posiada temperaturę Tsz.
4. Temperatura ośrodka na zewnątrz ścianki walcowej wynosi Tz.
5. Temperatura ośrodka wewnątrz ścianki walcowej wynosi Tw.
6. Rozważamy gęstość strumienia ciepła przewodzonego i przenikającego przez
ściankę walcową na jednostkę długości ścianki (gęstość liniowa).
Rys.3. Ścianka walcowa o grubości  i współczynniku przewodzenia 
a) Tw > Tz
b) Tw < Tz
Liniowa gęstość strumienia ciepła przewodzonego przez ściankę walcową
jednowarstwową można wyrazić wzorem:

Q
2
ql 

Tsw - Tsz 
rz
l
ln
rw
(13)
6
Rozkład temperatury w ściance walcowej przy =const można wyrazić wzorem:
T(r)  Tsw -
Tsw - Tsz
r
ln
r
rw
ln z
rw
(14)
przy =0(1+bT):
2
1
q
r 1

T(r)   Tsw   - l ln
b  0 b rw b

(15)
Liniowa gęstość strumienia ciepła przenikającego przez ściankę walcową
wielowarstwową między ośrodkami o temperaturach Tw i Tz może być
wyznaczona z następującej zależności:
q l   z Tw - Tz 
(16)
gdzie:
z 
2
n
1
1 r
1
  ln i 1 
rw w i 1  i
ri
rz z
6. Ustalone przewodzenie i przejmowanie ciepła przy istnieniu
wewnętrznych źródeł ciepła
Założenia:
1. Źródła ciepła są rozmieszczone równomiernie w rozpatrywanym ciele.
2. Wydajność źródła ciepła odpowiada objętościowej gęstości strumienia
ciepła o postaci:

Q
qv 
V
3. Ściana płaska o grubości  jest wykonana z materiału o współczynniku
przewodzenia ciepła .
4. Temperatury ośrodków stykających się ze ścianą z lewej i prawej strony
wynoszą odpowiednio Tp1 i Tp2, natomiast temperatury ścian Ts1 i Ts2.
5. Współczynniki przejmowania ciepła z lewej i prawej strony ściany wynoszą
odpowiednio 1 i 2.
6. Współrzędna x jest mierzona od powierzchni ścianki o temperaturze Ts1
w kierunku prostopadłym do ścianki.
7
Rozkład temperatury w ściance:
x q 2
T(x)  Ts1  Ts2 - Ts1   v

2
 x x2
   2
 

q

  Ts2  v  2 - x 2  1 T1 - Ts1    - x  (17)
2




Temperatury na powierzchniach ścianki:


  2

Tp 2   1  1  Tp 1  q v 




2

 2

 2

Ts1 
 
1 1  1

2
(18)

2 

Tp 1 - Tp 2 - q v 


2

 2
  qv 

  
2
1 2  2

1
(19)
Ts2  Tp 2
Jeżeli

Ts2 - Ts1    q v , to ciepło jest odprowadzane od obydwu powierzchni
q v
2
ścianki.
Maksimum temperatury występuje w punkcie o współrzędnej:
x0 

Ts2 - Ts1   
q v
2
(20)
i wynosi:
q v  2  Ts2 - Ts1  1
T0  Ts1 

 Ts2 - Ts1 
8
2q v 2
2
2
(21)
Jeżeli warunki brzegowe (,Ts,Tp) na obydwu powierzchniach ścianki są
jednakowe, wówczas współrzędną x mierzy się od środka ścianki, a jej grubość
oznacza się przez 2. W takim przypadku rozkład temperatury w ściance (17)
upraszcza się do postaci:
q v 2
T(x)  Ts 
2
  x 2 
1 -   
    
(22)
8
Maksymalna temperatura występuje wówczas w środku ścianki (x=0) i jest
równa:
q v 2
(23)
T0  Ts 
2
Gęstość strumienia ciepła na powierzchni ścianki:
q s   Ts - Tp   q v 
(24)
Temperatura powierzchni ścianki:
Ts  Tp  q v


(25)
W przypadku walca o promieniu rs i temperaturze ścianki Ts otoczonego
płynem o temperaturze Tp, rozkład temperatury w walcu wynosi:
2
2
q v rs   r  
T(r)  Ts 
1 -   
4   rs  


(26)
Maksymalna temperatura w osi walca (r=0):
q r
T0  Ts  v s
4
2
(27)
Gęstość strumienia ciepła na powierzchni walca:
q s   Ts - Tp  
q v rs
2
(28)
Temperatura powierzchni walca:
Ts  Tp 
q v rs
2
(29)
9
7. Nieustalone przewodzenie ciepła w ciałach stałych
Ponieważ pożar jest procesem dynamicznym (zapalenie i
rozprzestrzenianie się ognia), konieczne jest zastosowanie do jego opisu
matematycznego równań nieustalonej wymiany ciepła. Podstawowe równania
dla tego przypadku otrzymuje się w wyniku analizy bilansu strumienia ciepła w
nieskończenie małej objętości. Ma ono następującą postać (=const):
dT
q
 a 2 T  v
d
cp ρ
gdzie:  2T 
a
qv
(30)
 2 T  2T  2 T


- laplasjan temperatury
x 2 y 2 z 2
λ
c pρ
- współczynnik wyrównywania temperatury
- wydajność źródła ciepła
Wiele problemów udaje się sprowadzić do jednowymiarowej postaci drogą
wprowadzenia współrzędnych biegunowych lub cylindrycznych.
Dla jednowymiarowego procesu po odpowiednich przekształceniach
równanie (30) przyjmuje postać:
 2 T 1 dT q v

x 2 a d 
(31)
W większości procesów zakładamy, że qv=0. W takim przypadku
równanie (31) przyjmuje postać:
 2 T 1 dT

x 2 a d 
(32)
Na podstawie zależności (30) równanie przewodzenia nieustalonego w
ciałach stałych bez wewnętrznych źródeł ciepła można napisać w postaci:
  2T  2 T  2 T 
T
 a 2 
 2 
2


x

y
z 

(33)
Rozwiązanie powyższego równania zależy od warunków brzegowych.
10
Kąt nachylenia stycznej do krzywej rozkładu temperatury przy powierzchni
ciała stałego można wyznaczyć z następującej funkcji:
q Ts - Tp
 T 
tg  - 
  

 x  s 

(34)
Rys. 5. Interpretacja graficzna trzech rodzajów warunków brzegowych
związanych z przejmowaniem ciepła
a) warunek brzegowy pierwszego rodzaju
b) warunek brzegowy drugiego rodzaju
c) warunek brzegowy trzeciego rodzaju
Punkt kierujący O, przez który przechodzą wszystkie styczne do krzywych
rozkładu temperatury przy powierzchni ciała stałego, znajdują się w odległości
/ od powierzchni.
W praktyce rozróżnia się trzy rodzaje warunków brzegowych związanych
z przejmowaniem ciepła na powierzchni ciała stałego:
a) warunek brzegowy pierwszego rodzaju – znany jest rozkład temperatury we
wszystkich punktach powierzchni ciała (Ts), nie znana jest gęstość strumienia
a więc i kąt ,
b) warunki brzegowe drugiego rodzaju – znany jest rozkład gęstości strumieni
ciepła q, a zatem i kąt , we wszystkich punktach powierzchni ciała,
nie znana jest temperatura ścianki Ts,
c) warunki brzegowe trzeciego rodzaju – dana jest temperatura płynu Tp
otaczającego ciało stałe oraz współczynnik przejmowania ciepła ,
nie znana jest temperatura powierzchni ścianki Ts.
11
Ciało stałe o dużym współczynniku przewodzenia ciepła  i o małym
współczynniku przejmowania ciepła  jest w przybliżeniu w każdej chwili
izotermiczne [T(x)=const].
Nadwyżka T temperatury ciała T nad temperaturą płynu Tp wynosząca w
chwili początkowej wartość T0, zmienia się w czasie wg następującego
równania:

aA 
l

ΔT  T - Tp  ΔT0 exp - τ
 ΔT0 exp - Bi Fo 
 Vcp ρ 
L



(35)
αl
- liczba podobieństwa Biota
λ
aτ
Fo  2 - liczba podobieństwa Fouriera
l
λ
a
- współczynnik wyrównywania temperatury ciała stałego
ρ cp
gdzie: Bi 
l – charakterystyczny wymiar liniowy równy połowie grubości płyty
lub promieniowi walca albo kuli,
L=V/A – stosunek objętości ciała do pola powierzchni,
V – objętość ciała,
A – pole powierzchni,
 - gęstość,
cp – ciepło właściwe przy stałym ciśnieniu,
 - czas bieżący
Dla płyty nieograniczonej l/L=1, dla walca nieskończenie długiego l/L=2,
dla kuli l/L=3, dla sześcianu l/L=6, przy czym l – długość krawędzi.
Jeżeli Bi<0,1, to błąd wynikający z założonej izotermiczności ciała nie
przekracza 5%.
12