Wymiana ciepła

Podstawy wymiany ciepla
PODSTAWY WYMIANY CIEPŁA
1. Podstawowe pojęcia w wymianie ciepła
Sposoby transportu ciepła:

przewodzenie

konwekcja
- swobodna
- wymuszona

promieniowanie
Transport ciepła w ciałach stałych odbywa się na drodze przewodzenia. Z przewodzeniem
ciepła mamy do czynienia, gdy makroskopowe części ośrodka nie przemieszczają się względem siebie. Podstawowym sposobem transportu ciepła w płynach (cieczach i gazach) jest
konwekcja. W przypadku konwekcji płyn przemieszcza się i miesza. W płynach ciepło może
być też przewodzone. Gdy ruch płynu spowodowany jest różnicą temperatur w płynie, mamy
do czynienia z konwekcją swobodną. W przypadku konwekcji wymuszonej przemieszczanie
płynu wywołane jest przez pompę lub sprężarkę. Promieniowanie ciepła polega na transporcie
energii w postaci promieniowania elektromagnetycznego o określonej długości fal.
Pole temperatury
-
niestacjonarne (temperatura zależy od położenia elementu ciała oraz czasu)
T  f x, y, z, t 
-
(1.1)
stacjonarne (temperatura w danym punkcie ciała nie zależy od czasu)
T  f x, y, z 
(1.2a)
T
0
t
(1.2b)
Zagadnienie wymiany ciepła może być:
-
jednowymiarowe (temperatura zmienia się tylko względem jednej współrzędnej),
-
dwuwymiarowe (temperatura zmienia się tylko względem dwóch współrzędnych),
-
trójwymiarowe (temperatura zmienia się względem wszystkich współrzędnych).
2. Przewodzenie ciepła
2.1. Prawo Fouriera
2014-02-03 15:35:00
1/13
Podstawy wymiany ciepla
Prawo Fouriera wiąże gęstość strumienia przewodzonego ciepła w określonym punkcie ciała
z gradientem temperatury w tym punkcie
q   grad T   T
W 
 m2 
 
(2.1)
 W 
gdzie  
 jest współczynnikiem przewodzenia ciepła (przewodnością cieplną), którego
mK 
wartość zależy od rodzaju ciała, a także od temperatury.
Dla kartezjańskiego układu współrzędnych prostokątnych
grad T  T 
T
T
T
i
j
k
x
y
z
(2.2)
W prostokątnym układzie współrzędnych wektor q ma trzy składowe
q x  
T
x
(2.3a)
q y  
T
y
(2.3b)
q z  
T
z
(2.3c)
Rys. 2-1. Zakresy wartości współczynników przewodzenia ciepła.
2.2. Stacjonarne przewodzenie ciepła przez ściankę płaską przy   const
2014-02-03 15:35:00
2/13
Podstawy wymiany ciepla
Równanie różniczkowe opisujące ten przypadek przewodzenia (prawo Fouriera)
q  
dT
dx
(2.4)
Równanie (2.4) rozwiązujemy metodą rozdzielenia zmiennych
qdx  dT
(2.5)
Równanie (2.5) całkujemy stronami
x2
Tw 2
x1
Tw1
 qdx    dT
(2.6)
qx2  x1    Tw2  Tw1 
q
(2.7)

Tw1  Tw2 

(2.8)
gdzie   x2  x1 jest grubością ścianki przewodzącą ciepło.
Dla ścianki o powierzchni A
Q  Aq 

A

Tw1  Tw2 
(2.9)
Q
ATw1  Tw2 
(2.10)
2.2. Stacjonarne przewodzenie ciepła przez ściankę płaską wielowarstwową
2014-02-03 15:35:00
3/13
Podstawy wymiany ciepla
Do obliczenia strumienia ciepła przewodzonego przez ściankę wielowarstwową można użyć
wzoru (2.9) pod warunkiem, że współczynnik przewodzenia ciepła zostanie zastąpiony tzw.
zastępczym współczynnikiem przewodzenia ciepła
n
z 

i 1
n
i
(2.11)
i

i 1 i
gdzie:
i – numer warstwy
n – liczba warstw
δi – grubość warstwy o numerze i
λi – współczynnik przewodzenia ciepła dla warstwy o numerze i
2.3. Stacjonarne przewodzenie przez ściankę cylindryczną przy   const
2014-02-03 15:35:00
4/13
Podstawy wymiany ciepla
q  
dT
dr
W / m 
2
(2.12)
gdzie q zależy od promienia r
q
Q
Q

A 2rl
(2.13)
natomiast Q  const .
(2.13)  (2.12)
Q  2rl
W 
dT
dr
(2.14)
W równaniu (2.14) rozdzielamy zmienne i całkujemy równanie stronami
r2
T
w2
dr
Q   2l  dT
r
r1
Tw1
Q ln
Q
(2.15)
r2
 2l Tw 2  Tw1 
r1
(2.16)
2l
T  T   2dl Tw1  Tw2 
r2 w1 w 2
ln
ln 2
r1
d1
(2.17)
Strumień ciepła odniesiony do jednostki długości rury
2014-02-03 15:35:00
5/13
Podstawy wymiany ciepla
ql 
Q 2
Tw1  Tw2 

l ln d 2
d1
W / m
(2.18)
Dla ścianki wielowarstwowej
ql 
Q
2 z
T1  Tn1 

l ln d n1
d1
(2.19)
gdzie
d n 1
d1
z  n
1 d i 1
ln

di
i 1 i
ln
(2.20)
gdzie:
i – numer warstwy
n – liczba warstw
di – średnica warstwy o numerze i (pierwsza warstwa, o najmniejszej średnicy,
ma nr 1
λi – współczynnik przewodzenia ciepła dla warstwy o numerze i
3. Wnikanie (przejmowanie) ciepła
Wnikaniem ciepła nazywamy wymianę ciepła pomiędzy ścianką i omywającym ją płynem.
Równanie Newtona
2014-02-03 15:35:00
6/13
Podstawy wymiany ciepla
Q  A Tw  T f 
(3.1)
 W 
– współczynnik wnikania (przejmowania) ciepła
2
 m K 

 zależy od:
-
prędkości płynu: w,
-
od kształtu, wielkości, rodzaju i temperatury powierzchni wymiany ciepła: φ, l1, l2, ..., Tw,
-
od parametrów termofizycznych płynu: Tf, p, ρ, c, λ, υ.
  f w, T f , Tw , p,  , c,  , , , l1 , l2 , 
(3.2)
Np. dla przepływu wymuszonego cieczy lub gazu w kanale
Nu  C Rem Pr n
(3.3)
Np. dla przepływu burzliwego cieczy w kanale: m  0,8; n  0,4
Nu 
 dh

Re 
wd h


Pr 
a
- liczba Nusselta
(3.4)
- liczba Reynoldsa
(3.5)
- liczba Prandtla
(3.6)
Z (4)

a
 Nu
(3.7)
dh


m2 / s
 cp
 m2 / s
- współczynnik wyrównania temperatury
(3.8)
- współczynnik lepkości kinematycznej
2014-02-03 15:35:00
7/13
Podstawy wymiany ciepla
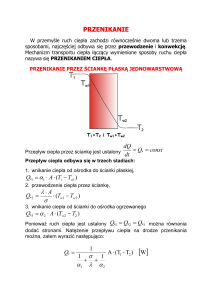
4. Przenikanie ciepła
Przenikaniem ciepła nazywamy transport ciepła od płynu o wyższej temperaturze do płynu o
niższej temperaturze przez przegrodę.
q  k T f 1  T f 2 
W/m 
2
(4.1)
 W 
gdzie k  2  jest współczynnikiem przenikania ciepła
m K
Dla ścianki o powierzchni A
Q  Aq
(4.2)
4.1. Przenikanie ciepła przez ściankę płaską o grubości 
Wnikanie ciepła do ścianki
q  1 T f 1  Tw1 
(4.3)
2014-02-03 15:35:00
8/13
Podstawy wymiany ciepla
Przewodzenie ciepła przez ściankę
q

T  T 
 w1 w 2
(4.4)
Przejmowanie ciepła przez płyn
q   2 Tw2  T f 2 
(4.5)
Z (4.3)
T f 1  Tw1 
q
(4.6)
1
Z (4.4)
Tw1  Tw 2 
q
(4.7)

Z (4.5)
Tw 2  T f 2 
q
(4.8)
2
Równania (4.6)-(4.8) sumujemy stronami
1 
1 
T f 1  T f 2  q   
 1   2 
q
1
 1
 
1   2
1
T
f1
(4.9)
 Tf 2 
(4.10)
Z porównania (4.10) z (4.1) otrzymujemy
1 1  1

 
k 1   2
(4.11)
4.2. Przenikanie ciepła przez ściankę cylindryczną
Q
ql 
l T f 1  T f 2 
(4.12)
1
1 d2
1

ln 
1d1 2 d1  2 d 2
Q
  kl T f 1  T f 2  W / m
l
(4.13)
2014-02-03 15:35:00
9/13
Podstawy wymiany ciepla
W 
gdzie kl 
jest liniowym współczynnikiem przenikania ciepła
 mK 
1
1
1 d2
1


ln 
kl 1d1 2 d1  2 d 2
(4.14)
5. Obliczanie wymienników ciepła
Pojemność cieplna czynnika W  m c p
2014-02-03 15:35:00
10/13
Podstawy wymiany ciepla
Bilans energetyczny wymiennika ciepła
 1c p1 T1'  T1"   m
 2c p 2 T2"  T2' 
Q  m
(5.1a)
Q  W1 T1'  T1"   W2 T2"  T2' 
(5.1b)
Równanie wymiany ciepła
2014-02-03 15:35:00
11/13
Podstawy wymiany ciepla
Q  kA0 Tsr
(5.2)
Średnia różnica temperatur
 T  A  T  AdA

A0
Tsr
0
1
2
(5.3)
A0
Średnia różnica temperatur dla wymienników współprądowych i przeciwprądowych
Tsr 
T ' T "
T '
ln
T "
(5.4)
gdzie:
T '  T1'  T2' ; T "  T1"  T2" - dla współprądu
(5.5a)
T '  T1'  T2" ; T "  T1"  T2' - dla przeciwprądu
(5.5b)
Dla określonych temperatur wlotowych i wylotowych średnia różnica temperatur jest największa przy przepływie przeciwprądowym, a najmniejsza dla przepływu współprądowego.
Średnia różnica temperatur dla wymienników o przepływie krzyżowo prądowym i mieszanym
leży w przedziale pomiędzy średnią dla współprądu i przeciwprądu
Tsrpp  Tsrm  Tsrwp
(5.6)
Średnią różnicę temperatur dla wymienników o przepływie krzyżowym i mieszanym można
wyznaczyć wykorzystując poprawkę εΔT
Tsrm  Tsrpp T
(5.7)
gdzie
1   T  0
(5.8)
 T  f P, R 
(5.9)
P
T2"  T2'
T1'  T2'
(5.10a)
R
T1'  T1"
T2"  T2'
(5.10b)
2014-02-03 15:35:00
12/13
Podstawy wymiany ciepla
Każdy typ wymiennika ma swój wykres poprawek  T  f P, R  .
2014-02-03 15:35:00
13/13