Wstęp do fizyki Słońca – Lista zadań numer 4

Wstęp do fizyki Słońca – Lista zadań numer 4
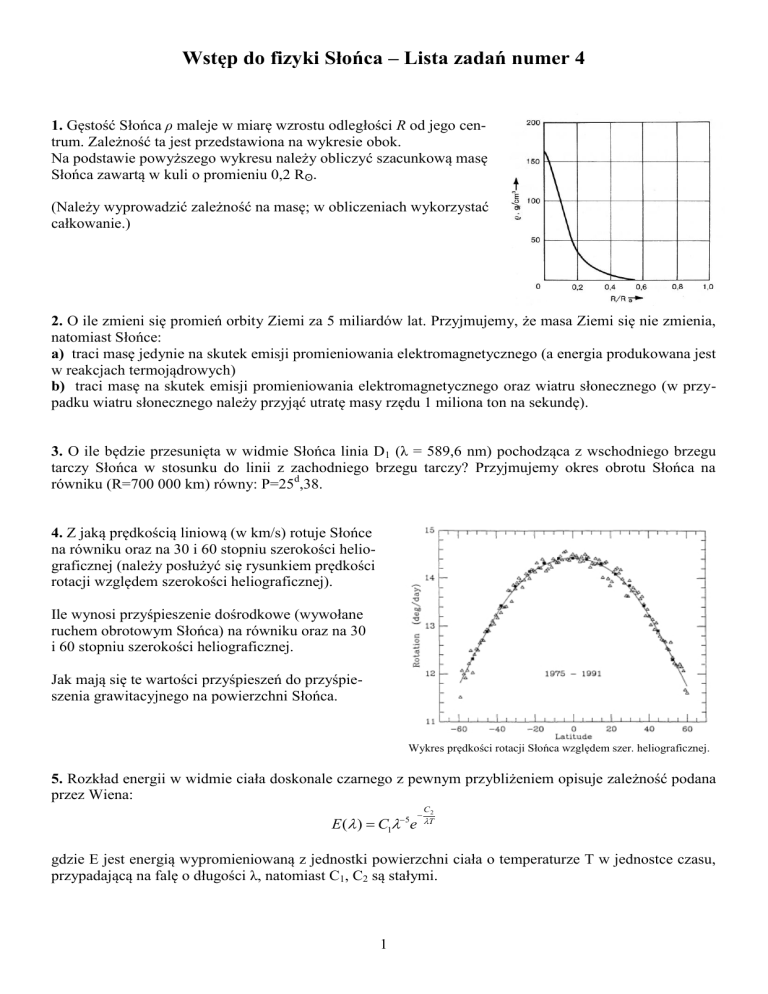
1. Gęstość Słońca ρ maleje w miarę wzrostu odległości R od jego centrum. Zależność ta jest przedstawiona na wykresie obok.
Na podstawie powyższego wykresu należy obliczyć szacunkową masę
Słońca zawartą w kuli o promieniu 0,2 Rʘ.
(Należy wyprowadzić zależność na masę; w obliczeniach wykorzystać
całkowanie.)
2. O ile zmieni się promień orbity Ziemi za 5 miliardów lat. Przyjmujemy, że masa Ziemi się nie zmienia,
natomiast Słońce:
a) traci masę jedynie na skutek emisji promieniowania elektromagnetycznego (a energia produkowana jest
w reakcjach termojądrowych)
b) traci masę na skutek emisji promieniowania elektromagnetycznego oraz wiatru słonecznego (w przypadku wiatru słonecznego należy przyjąć utratę masy rzędu 1 miliona ton na sekundę).
3. O ile będzie przesunięta w widmie Słońca linia D1 (λ = 589,6 nm) pochodząca z wschodniego brzegu
tarczy Słońca w stosunku do linii z zachodniego brzegu tarczy? Przyjmujemy okres obrotu Słońca na
równiku (R=700 000 km) równy: P=25d,38.
4. Z jaką prędkością liniową (w km/s) rotuje Słońce
na równiku oraz na 30 i 60 stopniu szerokości heliograficznej (należy posłużyć się rysunkiem prędkości
rotacji względem szerokości heliograficznej).
Ile wynosi przyśpieszenie dośrodkowe (wywołane
ruchem obrotowym Słońca) na równiku oraz na 30
i 60 stopniu szerokości heliograficznej.
Jak mają się te wartości przyśpieszeń do przyśpieszenia grawitacyjnego na powierzchni Słońca.
Wykres prędkości rotacji Słońca względem szer. heliograficznej.
5. Rozkład energii w widmie ciała doskonale czarnego z pewnym przybliżeniem opisuje zależność podana
przez Wiena:
E ( )  C15e

C2
T
gdzie E jest energią wypromieniowaną z jednostki powierzchni ciała o temperaturze T w jednostce czasu,
przypadającą na falę o długości λ, natomiast C1, C2 są stałymi.
1
Traktując gwiazdę jako ciało doskonale czarne oraz posługując się podaną zależnością Wiena, należy
znaleźć wzór na temperaturę gwiazdy, dla której stosunek wartości energii wypromieniowanej jako fale
E
o długości λ1 i λ2 (z jednostki powierzchni i w jednostce czasu) wynosi 1 .
E2
6. Udowodnić, że ciśnienie promieniowania światła słonecznego wywierane na cząsteczki znajdujące się
w warkoczu komety, wyraża się wzorem:
P
E
1   
c
gdzie: P – ciśnienie światła, E – ilość energii promienistej padającej na jednostkę powierzchni w jednostce
czasu,  – współczynnik odbicia światła (albedo), c – prędkość światła w próżni.
=> W obliczeniach należy przyjąć korpuskularną teorię światła.
7. Ciśnienie promieniowania słonecznego P wyraża się wzorem:
P
E
1   
c
gdzie:
E – jest odpowiednikiem stałej słonecznej w danej odległości od Słońca,
 – współczynnik odbicia światła (albedo), c – prędkość światła.
Jaki powinien być promień r0 kulistej bryłki materii o danej gęstości μ i albedo ρ, aby siła
grawitacyjna przyciągania tej bryłki przez Słońce była równoważona przez ciśnienie promieniowania
słonecznego?
Jaki będzie los (w Układzie Słonecznym) takiej materii skupionej w bryłkach o promieniu r < r0 ?
Przyjmujemy jako dane: masę Słońca = M, stałą słoneczną w odległości 1 AU = E0 .
Krzysztof Radziszewski
2