Rozdział 7
Molekuły
7.1: Jak się formują molekuły?
7.2: Wiązania molekularne
7.3: Rotacje
7.4: Wibracje
7.5: Spektra
7.6: Złożone płaskie molekuły
Johannes Diderik van der Waals
(1837 – 1923)
“Nie, ta sztuczka się nie uda... Jak można wytłumaczyć prawami chemii i fizyki
tak ważny biologiczny fenomen, jakim jest pierwsza miłość...”
Albert Einstein
“Myślenie nie wyklucza emocji. Wręcz przeciwnie. Ja myślę o emocjach. Chcę
zrozumieć ich pochodzenie. Stąd tyle chemii i molekuł w moich tekstach.”
Janusz Leon Wiśniewski
Przygotowanie Marek Szopa, na podstawie Rick Trebino, Georgia Tech, www.physics.gatech.edu/frog/lectures
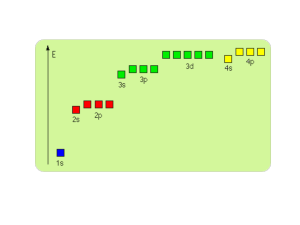
Molekuły są złożone z
(wieloelektronowych) atomów
Kiedy mamy do czynienie więcej niż jednym atomem, funkcje falowe i
potencjały zależą od położeń wszystkich nukleonów i elektronów.
V = V (r1 , r2 ,..., rN )
Ψ = Ψ (r1 , r2 ,..., rN , t )
Rozwiązanie równania Schrodingera
jest w tym przypadku trudniejsze niż
dla atomów wieloelektronowych.
Potrzebne są zaawansowane metody
poszukiwania rozwiązań
przybliżonych. W tym miejscu
zaczyna się Chemia Kwantowa.
7.1: Wiązania molekularne a spektra
Nukleon
Jedyną siłą, która
wiąże atomy
w molekuły jest
siła Kulomba.
Nukleon
E=0
Chmura
elektronów
Chmura
elektronów
Czyż jednak atomy nie są elektrycznie obojętne? Tak!
Rzeczywiście, sferycznie symetryczne atomy nie przyciągają się –
ładunki dodatnie i ujemne działają jak punktowe, skoncentrowane
w centrum atomu a ich siły wzajemnie się znoszą.
W jaki zatem sposób powstają molekuły?
Przyczyna powstawania molekuł
Większość atomów nie jest
sferycznie symetryczna.
Na przykład – te dwa „atomy”
przyciągają się!
Atom #1
Atom #2
−
+
+
−
Kombinacja sił przyciągających i odpychających jest w stanie
utworzyć stabilna strukturę molekuły.
Siła jest proporcjonalna do gradientu energii potencjalnej,
F = −dV/dr, gdzie r to położenie.
Ładunek większości atomów jest
rozmieszczony nierównomiernie.
Gęstość prawdopodobieństwa rozkładu elektronów dla trzech
różnych stanów atomu wodoru.
Zamknięte powłoki elektronowe są
sferycznie symetryczne.
Atomy o zamkniętych powłokach (gazy szlachetne)
najtrudniej zjonizować.
Ionization
energy (eV)
Energia jonizacji
Noble
gases (difficult
to
Gazy szlachetne
(trudno
zremove
nich usunąć
elektron)
an electron)
Atomic
Liczba number
atomowa(Z)
(Z)
Atomy o zamkniętej powłoce
(gazy szlachetne) mają
również najmniejszy promień.
Promień atomowy (nm)
Atomy o zamkniętej
powłoce elektronowej
Liczba atomowa (Z)
Gazy szlachetne (o ile nie są w znaczący sposób zmienione)
nie tworzą molekuł
.
Zamknięta powłoka elektronowa
jest stabilna.
Atomy posiadające jeden lub dwa (a nawet więcej)
dodatkowych elektronów mogą je oddać innym atomom, aby
im umożliwić zamkniecie powłoki elektronowej.
Atomy o takim
nadmiarze
elektronów są
nazywane
elektrododatnimi
Te które cechuje
niedobór
elektronów
nazywamy
elektroujemnymi
Wiązania jonowe
Atomy elektrododatnie oddają
elektrony atomom
elektroujemnym.
Przykład: Sód (1s22s22p63s1) Łatwo
oddaje swój elektron 3s
aby zjonizować się do Na+,
podczas gdy chlor
(1s22s22p63s23p5) łatwo
przyjmuje elektron stając się Cl−.
atomy
Przekazanie
elektronu
jon
dodatni
jon
ujemny
Wiązanie jonowe
Wiązania
kowalencyjne
Dwa atomy elektroujemne,
których elektrony tworzą
ujemnie naładowaną chmurę
pomiędzy dodatnio
naładowanymi jądrami
Przykład: Molekuły złożone z
dwu takich samych atomów
mają zwykle wiązanie
kowalencyjna
Większe molekuły uformowane
z wiązań kowalencyjnych:
atomy
Współdzielenie
elektronów
molekuła
Diament
Wiązanie
kowalencyjne
Wiązania Van der Waalsa
Słabe wiązania pomiędzy
dipolami trwałymi lub
indukowanymi,
występujące w cieczach
lub ciałach stałych
Przykład: w graficie
wiązania van der Waalsa
łączą sąsiednie
płaszczyzny grafenowe
atomów węgla.
Płaszczyzny te przy
niewielkim tarciu mogą
ślizgać się względem
siebie. Grafen z ołówka
łatwo odrywa się i
przylega do papieru.
Wiązanie wodorowe
Jeśli atom wodoru jest związany
kowalencyjnie z jednym
elektroujemnym atomem, może
jednocześnie tworzyć takie wiązanie
z drugim łącząc je w jedną molekułę
Wiązanie wodorowe (5 do 30 kJ/mol)
jest silniejsze od wiązania van der
Waalsa ale słabsze od wiązań
kowalencyjnych lub jonowych.
W idealnie czystej wodzie, w
temperaturze 4 °C, cz ąsteczki wody
tworzą "paczki", składające się ze
średnio siedmiu cząsteczek
powiązanych tymi wiązaniami.
Wiązanie
wodorowe
Atomy
elektroujemne
Wiązania metaliczne
Elektrony walencyjne w metalach są słabo związane z jądrami i
tworzą wolną chmurę, która przewodzi prąd ale jednocześnie wiąże
w krystalicznej sieci dodatnio naładowane jądra. W modelu metalu
Drudego mamy gaz swobodnych elektronów !
Jony metalu
Elektrony swobodne
Wiązania molekularne a spektra
Potencjał, który czuje jeden atom w pobliżu
drugiego jest w przybliżeniu równy:
A B
V= n− m
r r
gdzie A i B są dodatnimi stałymi.
Potęgi n oraz m są różne od jedności z powodu ekranującego
oddziaływania różnych powłok elektronowych.
W rezultacie, jeśli n > m
może powstać stabilna
równowaga odpowiadająca
energii całkowitej E < 0.
Kształt krzywej zależy od
parametrów A, B, n, i m.
Wiązania molekularne a spektra
Wiązanie pary atomów.
Aby rozdzielić parę na dwa odrębne
atomy należy dostarczyć im tyle
energii aby całkowita energia układu
była równa zeru.
Energia
wiązania
Odległość
równowagi
Wartość odległości r odpowiadająca
minimum jest odległością
równowagi. Wartość energii E
potrzebnej do całkowitego
rozdzielenia dwu atomów jest zwana
energią wiązania. Energia ta jest w
przybliżeniu równa głębokości studni
potencjału.
Wielkość energii E zależy od temperatury gdyż wpływają na nią
zależne od temperatury drgania atomów.
Stany wibracyjne
Pod wpływem temperatury energia kinetyczna atomów tworzących
cząsteczki prowadzi do powstania stanów wibracyjnych. Stany te
można wzbudzić również za pomocą światła.
Załóżmy, że dwa atomy to punktowe
masy, które połączone za pomocą
bezmasowej sprężyny wykonują
drgania harmoniczne.
Stany wibracyjne: prosty oscylator
harmoniczny
Prosty oscylator harmoniczny
dobrze opisuje drgania molekuł
zarówno dwuatomowych jak i
bardziej złożonych
Stany wibracyjne
Poziomy energetyczne
z kwantowo oscylatora
harmonicznego
Ewibr = (n + 1 2 ) ℏω
n nazywa się
wibracyjną liczbą
kwantową. Nie
należy jej mylić z
główną liczbą
kwantową n,
elektronu.
Reguła wyboru dla przejścia
wibracyjnego:
∆n = ±1
Jedyną linią spektralną pozostaje ℏω !
Odchylenia od doskonałego potencjału
parabolicznego prowadzą również do
innych przejść pochodnych, ale są one
znacznie słabsze.
Wibracje wody
Libracje
Symetryczne
rozciąganie
Asymetryczne
Asymetryczne
rozciąganie
rozciąganie
Zginanie
A by chronić pry watność uży tk ownik a, program PowerPoint zablok ował automaty czne pobranie tego obrazu.
Stany wibracyjne CH2
Wiązania wodorowo-węglowe są bardzo ważne dla chemii
materii ożywionej
Symetryczne
rozciąganie
Antysymetryczne
rozciąganie
Zginanie
Kolebanie
Balansowanie
Skręcanie
Stany rotacyjne
Rozważmy dwuatomową molekułę.
Cząsteczki dwuatomowe mogą być traktowane jako dwa atomy
połączone bezmasowym sztywnym prętem (model sztywnego
rotatora).
W tym, czysto rotacyjnym systemie, energia kinetyczna jest
wyrażone poprzez moment pędu i moment bezwładności .
Erot
L2
=
2I
Stany rotacyjne
L jest skwantowany.
L = ℓ(ℓ + 1) ℏ
Więc dopuszczalne poziomy energetyczne
również:
Erot
ℏ 2 ℓ (ℓ + 1)
=
2I
Erot zależy tylko od liczby kwantowej
całkowitego momentu pędu ℓ.
Energia
Stany rotacyjno wibracyjne
Możliwe jest jednoczesnie wzbudzenie stanów rotacji obrotowej i
wibracji. Całkowita energia stanu rotacyjno-wibracyjnego jest:
E = Erot + Evibr
ℏ 2 ℓ (ℓ + 1)
1
=
+ n + ℏω
2I
2
Energie stanów wibracyjnych są rozmieszczone w regularnych
odstępach.
Przejście od stanu + 1 do :
2
ℏ
Energia fotonów będzie
E fot = [ (ℓ + 1)(ℓ + 2) − ℓ (ℓ + 1) ]
2I
wzrastała proporcjonalnie
ℏ2 2
ℏ2
Do liczby kwantowej ,
2
ℓ + 3ℓ + 2 − ℓ − ℓ = (ℓ + 1)
=
(plus różnica energii wibracji)
2I
I
Stany
rotacyjno
wibracyjne
∆E wzrasta liniowo z ℓ.
Wiele przejść jest
zabronionych przez reguły
wyboru, że ∆ℓ = ±1 i ∆n = ±1
Różnice energii wibracji są
większe niż energie rotacji
Stany rotacyjno wibracyjne
Odstępy częstotliwości emisji (i absorpcja) zależą od ℓ. Im wyższy
wyjściowy poziom energii tym większa energia fotonu.
Energie wibracji są większe niż energie rotacji. Dla cząsteczki
dwuatomowej, to różnica energii jest widoczna w strukturze
pasmowej.
Intensywność linii zależy od obsadzenia stanów i reguł wyboru dla
przejść wibracyjnych.
∆n = 3
∆n = 2
∆n = 1
Długość fali →
∆n = 0
Spektrum Rotacyjno/Wibracyjne
W widmie absorpcyjnym HCl, odstępy między wierzchołkami
mogą być wykorzystane do obliczenia momentu bezwładności I
molekuły. Brakujący szczyt w centrum spektrum odpowiada
zabronionemu przejściu ∆ℓ = 0.
ℓi− ℓf > 0
Intensywność
ℓi− ℓf < 0
ni− nf = 1
Częstotliwość (10 Hz)
Częstości drgań atomów i molekuł
Elektrony wibrują w swoim ruchu wokół nukleonów
Wysoka częstotliwość: ~1014 - 1017 razy na sekundę.
Nukleony w molekułach wibrują
w swoim ruchu względem siebie
Pośrednia częstotliwość:
~1011 - 1013 razy na sekundę.
Nukleony w molekułach rotują
Niska częstotliwość: ~109 - 1010 razy na sekundę.
Włączając elektronowe poziomy energetyczne
Typowe poziomy
energetyczne dużej molekuły
E = Eelektronowe + Ewibracyjne. + Erotacyjne
2-gi wzbudzony
poziom elektronowy
Energia
1-szy wzbudzony
poziom elektronowy
Najniższy rotacyjnowibracyjny poziom danej
„rozmaitości” elektronowej
Wzbudzony rotacyjnowibracyjny poziom
Przejście
Elektronowy
stan podstawowy
Jest wiele innych złożonych
efektów jak np.: sprzężenie
spin-orbita, oddziaływanie
ze spinem jądrowym, które
dodatkowo rozszczepiają
poziomy.
W rezultacie widma cząsteczkowe są z reguły bardzo skomplikowane.
Badanie widm rotacyjno-wibracyjnych
Spektroskopia FTIR (Fourier
transform infrared):
Dzięki zastosowaniu interferometru
Michelsona z ruchomym lustrem można
badać transformatę Fouriera widm
podczerwonych
Foton rozproszony
Foton padający
∆E
Opóźnienie
Rozpraszanie Ramanowskie:
Molekuła absorbując foton o pewnej
energii, może wypromieniować foton
nieznacznie zmienionej energii ±∆E
(większej lub mniejszej) oddając lub
przyjmując swoja energię rotacyjną lub
wibracyjną.
W tym przypadku reguła wyboru dla
momentu pędu może być ∆ℓ = ±2.
Modelowanie złożonych molekuł
Zdarza się, że bardziej
skomplikowane jest tak naprawdę
łatwiejsze!
Duże molekuły organiczne (opartych
na węglu) często są płaskie, a
najsłabiej związane elektrony mogą
w zasadzie swobodnie poruszać po
całym obwodzie. Nazywamy to
Modelem Wolnych Elektronów
Obwodowych.
Jądro i
elektrony
wewnętrz
ne
Ścieżka elektronów
zewnętrznych
To tak jak cząstka w jednowymiarowym polu! Stanami własnymi są
fale sinusoidalne. Jedyną różnicą jest to, że x = L jest taka sama jak
x = 0. Więc ψ nie musi być zero na granicy i jest dodatkowy stan, o
najniższej energii, którym jest funkcja stała:
ψ 0 ( x) = 1/ L