E Ruch ladunku w polu elektrycznym

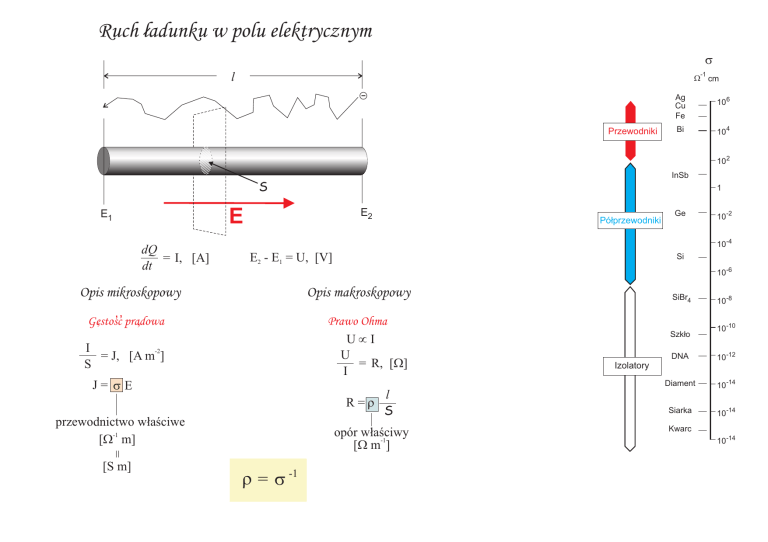
Ruch ladunku w polu elektrycznym
s
-1
l
W cm
Przewodniki
Ag
Cu
Fe
10 6
Bi
10 4
10 2
InSb
S
1
E2
E
E1
dQ
= I, [A]
dt
Ge
10 -2
10 -4
Si
E2 - E1 = U, [V]
10 -6
Opis makroskopowy
Opis mikroskopowy
,,
,
Gestosc
pradowa
,
Prawo Ohma
UµI
U
= R, [W]
I
I
= J, [A m-2]
S
J= sE
R =r
przewodnictwo właściwe
[W-1 m]
l
S
opór właściwy
[W m-1]
=
[S m]
Półprzewodniki
r = s -1
SiBr4
Szkło
10 -8
10 -10
DNA
10 -12
Diament
10 -14
Siarka
10 -14
Izolatory
Kwarc
10 -14
Typy kryształów
typ
kryształ
kowalencyjny
kryształ
jonowy
kryształ
molekularny
kryształ
metaliczny
gaz
elektronowy
sieć
krystaliczna
anion
jon metalu
kation
Przykład
Energia
kohezji *
oddziaływania
coulombowskie
uwspólniona
para elektronów
NaCl
LiF
diament
krzem
H20 - lód
CH4 - zestalony
7,4 eV/atom
4,6 eV/atom
0,6 eV/cząst.
0,1 eV/cząst.
3,3 eV/atom
4,5 eV/atom
oddziaływania
międzycząsteczkowe
*) energia kohezji kryształu - energia potrzebna do wyrwania atomu (cząsteczki) z sieci krystalicznej
Na
Fe
1,1 eV/atom
~ 4 eV/atom
Metale - model Drudego
tzw. Model gazu elektronowego
Model klasyczny metali opracowany około 1900 r. przez Drudego
1
metal stanowi sieć krystaliczną kationów
"zanurzoną w morzu" elektronów swobodnych
nazywanym też "gazem elektronowym".
gaz
elektronowy
jon metalu
2
poruszające się "swobodnie" elektrony ulegają
rozpraszaniu w wyniku zderzeń ze zrębami
krystalicznymi (kationami metali).
e-
3
+
Me
Droga swobodna, czyli odległość pomiędzy kolejnymi zderzeniami
jest rzędu stałej sieciowej, t.j. odległości pomiędzy zrębami
krystalicznymi (czyli około 1-2 Å).
zakłada się brak sprzężeń elektron-elektron
czyli tak jakby elektrony nie widziały się nawzajem
tor ruchu
elektronu
jon metalu
4
Elektrony "drudego" traktowane są jako izolowane cząstki klasyczne o energii
kinetycznej 3/2 kT (po 1/2 kT na każdy stopień swobody)
Model Drudego (2)
Podstawowe właściwości fizyczne metali a model drudego:
1. Srebrzystoszare (oprócz Cu i Au) i błyszczące.
hv
hv
2. Kowalne
mała siła kohezji powoduje ze
zręby krystaliczne łatwo mogą
ulegać przemieszczeniu względem
siebie.
3. Łatwo tworzą stopy
4. Dobre przewodniki ciepła
5. Dobre przewodniki elektryczności
Model Drudego (tzw. model gazu elektronowego) dobrze opisuje jakościowo właściwości
fizyczne metali.
Model ten zawodzi, natomiast, w przypadku prób ilościowego opisu:
-właściwości termicznych,
-właściwości magnetycznych,
-właściwości elektromagnetycznych.
Np. jeśli przyjąć, zgodnie z modelem Drudego, że każdy elektron w danej temperaturze
(T) posiada energię kinetyczną równą 3/2 kT, to wartość ciepła właściwego metalu była by
o kila rzędów wyższa niż rzeczywiście mierzona eksperymentalnie.
Analogicznie podatność magnetyczna czy przewodnictwo elektryczne i jego zależność
temperaturowa przewidywane na podstawie modelu Drudego daleko odbiegają od
wartości rzeczywistych.
Na podstawie danych doświadczalnych można by dojść do wniosku, że tylko 1/10 000
elektronów drudego ma wpływ na wymienione wyżej w właściwości.
próżnia
EA
Pasmo przewodnictwa
3s
IP
2p
EF
Eg
2s
1s
Pasmo walencyjne
Odległość międzyatomowa
izolowane
atomy
kryształ
(cząsteczka)
Eg - wielkość przerwy wzbronionej
EA - Powinowactwo elektronowe
EF - poziom Fermiego
IP - potencjał jonizacji
BW - szerokość pasma
BW
Poziom Fermiego
Rozkład Fermiego-Diraca mówi nam ile z pośród dostępnych poziomów energetycznych jest obsadzone elektronami.
f (E) =
1
1 + exp{(E-EF)/kT}
EF – Energia poziomu Fermiego
k – stała Boltzmanna = 1.38 1023 J/K = 8.6 105 eV/K
T – temperatura bezwzględna K
T®0K
T>0K
f ( E > EF ) =
1
= 0
1 + exp (+Ą)
f ( E < EF ) =
1
= 1
1 + exp (- Ą)
f (E)
E - EF
kT
>> 1
f (E) ® 0
E - EF
kT
E - EF
E = EF - 3kT: exp
kT
= 1
f (E) = 1/2
E = EF + 3kT: exp
E = EF :
exp
1
0,5
0
EF
EF - 3kT
E
EF + 3kT
<< 1
f (E) ® 1
Energia elektronu
wyliczona na podstawie równań mechaniki kwantowej
Elektron quasi-swobodny
w polu periodycznym
Elektron swobodny
8p2m0
Ey
-k y =
h2
2
amplituda
eikx
E
Na
+
y(x)
pasmo dozwolone
pasmo wzbronione
pasmo dozwolone
k
pasmo wzbronione
pasmo dozwolone
pasmo wzbronione
pasmo dozwolone
k- liczba falowa
y- funkcja falowa
-5 pa
-3 pa
- pa
0 pa
Strefa
Brillouina
3 pa
5 pa
k
METALE
Me II
np.: Be
Me I
np.: K
E
PÓŁPRZEWODNIKI
i IZOLATORY
E
pasmo
Przewodnictwa
Eg> 3 eV : izolatory
pasmo
Przewodnictwa
EF
pasmo
wzbronione
pasmo
Przewodnictwa
pasmo
walencyjne
EF
Eg
Eg< 3 eV : półprzewodniki
Podstawowe wzory na przewodnictwo elektryczne
1. Przewodnictwo elektryczne
zależy od liczby nośników prądu oraz ich ruchliwości
s = neeme
s - przewodnictwo właściwe
ne - ilość elektronówswobodnych w jednostce objętości
e - ładunek nośnika
me- ruchliwość nośnika ładunku, średnia prędkość jaką nabywa elektron
o masie me i w czasie t, w polu jednostkowym
et
me = m
e
W przypadku półprzewodników często mamy do czynienia z układami,
które posiadają zarówno swobodne elektrony jak i dziury
przewodnictwo samoistne: polega na samoistnym (najczęściej termicznym) wzbudzeniu elektronu
z pasma przewodnictwa powstaje wtedy para elektron - dziura
+
nd = ne
przewodnictwo w takich przypadkach określane jest za pomocą wzoru:
s = neeme + ndemd
md i nd oznaczają odpowiednio ruchliwość i stężenie dziur
Zależność temperaturowa przewodnictwa
Półprzewodniki (w tym również polimery przewodzące) wykazują wzrost przewodnictwa elektrycznego
ze wzrostem temperatury
  EA 
  o exp 

 kB T 
  Eg 
  o exp 

2kB T 
EA - termiczna energia aktywacji przewodnictwa elektrycznego
Eg - wielkość przerwy energetycznej, (odległość pomiędzy "wierzchołkiem"
pasma walencyjnego, a "dnem" pasma przewodnictwa)
W odróżnieniu od przewodników metalicznych półprzewodniki nie posiadają
elektronów swobodnych.
W związku z tym nie ma efektu rozpraszania elektronów na drgających zrębach
sieci krystalicznej odpowiedzialnych za obniżenie przewodnictwa ze wzrostem
temperatury.
W półprzewodnikach istotnym czynnikiem wpływającym na przewodnictwo jest
liczba nośników ładunku powstałych w wyniku wzbudzenia elektronów ze stanu
podstawowego.
Obok wzbudzenia elektrony mogą przeskoczyć do pasma przewodnictwa również
na drodze tunelowania przez barierę potencjału przerwy wzbronionej.
Prawdopodobieństwo tunelowania wzrasta wraz ze wzrostem temperatury.
Wzrost temperatury powoduje zatem wzrost liczny par nośników ładunku elektrondziura
Wpływ domieszkowania na przewodnictwo
Procesy domieszkowania, powodują generowanie tzw.
nadmiarowych nośników ładunku.
Nośniki samoistne zawsze powstają w postaci pary elektron dziura
i znajdują się w stanie równowagi dynamicznej Kreacji- Anihilacji.
Równowaga ta zależy od temperatury. Nośniki nadmiarowe to
samodzielne elektrony lub dziury generowane przez oddziaływanie
domieszki z półprzewodnikiem i ich liczność zależy od stężenia
domieszki w materiale oraz jej charakteru chemicznego.
+
DOMIESZKOWANIE LEKKIE
typu - p
typu - n
pasmo Przewodnictwa
pasmo Przewodnictwa
poziom Donorowy
+
+
poziom Akceptorowy
pasmo Walencyjne
pasmo Walencyjne
DOMIESZKOWANIE SILNE
pasmo Przewodnictwa
pasmo Przewodnictwa
pasmo Donorowe
+ + + + + + + + + +
pasmo Walencyjne
pasmo Akceptorowe
pasmo Walencyjne
Nowe pojęcia
! Nośnik ładunku
! Nośnik nadmiarowy
! Nośniki samoistne
! Domieszkowanie typu-n i typu-p
! poziom i pasmo akceptorowe
! poziom i pasmo donorowe
Polimery przewodzące
Polimer - (gr. polymeres - wieloczęściowy).
Wielkocząsteczkowy związek chemiczny o charakterystycznej budowie molekularnej.
Zbudowany jest z wielokrotnie powtórzonych segmentów o identycznej budowie zwanych
merami.
Poszczególne mery są ze sobą połączone wiązaniami chemicznymi tworząc długie łańcuchy
o zróżnicowanej budowie.
Polimery powstają w rekcji polimeryzacji ze związków prostych zwanych monomerami.
Np.: polietylen
n H2C
H2
C
CH 2
C
H2
H2
C
C
H2
H2
C
C
H2
H2
C
CH 2
C
H2
n
polietylen
etylen
polimer przewodzący
Związek polimerowy zdolny do przewodzenia prądu elektrycznego.
Do połowy XX w. uważano, że polimery podobnie jak większość związków organicznych są
dielektrykami, czyli substancjami niezdolnymi do przewodzenia prądu elektrycznego.
(grupa izolatorów).
Pierwszym odkrytym polimerem przewodzącym był poliacetylen
+
HC
CH
CH
CH
... +
+
HC
HC
+
HC
CH
CH
CH
+
+
HC
+ ...
HC
acetylen
HC
CH
CH
CH
HC
HC
HC
poliacetylen
CH
CH
CH
HC
HC
Polimery przewodzące (2)
Historia
Giulio Natta (1903 - 1979)
W roku 1958 przy okazji testowania katalizatorów Zieglera-Natty otrzymał czarny
nierozpuszczalny proszek, ulegający dekompozycji na powietrzu. Był to
poliacetylen PA.
W owym czasie nikt się tym przypadkowym produktem nie zainteresował
1962 r.
Pople i Walmsley zwracają uwagę na możliwość występowania defektów w długich łańcuchach
polimerów. Zasugerowali oni, że defekty takie mogą być odpowiedzialne za duże stężenie wolnych
spinów rejestrowane w przypadku skoniugowanych polimerów (np.: w trans-PA jeden spin przypada
średnio na każde 3000 atomów węgla)
Hideki Shirakawa (ur. 1936 w Tokio)
Wraz z Skuim Ikedą w roku 1971 po raz pierwszy otrzymują cienką folię PA,
prowadząc polimeryzację acetylenu na powierzchni stężonego roztworu
katalizatorów Zieglera - Natty.
Otrzymany polimer był nierozpuszczalny w znanych rozpuszczalnikach oraz bardzo
wrażliwy na działanie tlenu i wilgoci. Posiadał metaliczny połysk i wykazywał
budowę fibrylarną. Pod wpływem rozciągania ulegał częściowej orientacji.
1980 r.
Wagner opracowuje metodę syntezy poliacetylenu na bazie katalizatorów Luttingera (mieszanina
Co(NO3)2 i NaBH4) otrzymuje cienki film polimerowy.
Edwards i Feast opracowują nową metodę syntezy poliacetylenu z prekursora, którego termiczny
rozkład prowadzi do otrzymania czystego PA. Metodę nazwano Durham - Graz.
Otrzymany tą metodą polimer wolny jest od zanieczyszczeń katalizatorem. W czasie termicznej
eliminacji temperatura powoduje zmianę stosunku izomerów cis i trans.
Rok 2000:
Nagroda Nobla w dziedzinie Chemii za odkrycie i badania polimerów przewodzących
The Nobel Prize in
Chemistry 2000
"for the discovery and development of
conductive polymers"
Hideki
Shirakawa
Alan J.
Heeger
Alan G.
MacDiarmid
Polimery przewodzące (3)
Przykłady
Polimer
Typowe
domieszki
Wzór
Poliacetylen (PA)
n
Przewodnictwo
domieszkowanego
W-1cm-1
I2, Br2, Li, Na,
AsF5
10000
BF4-, ClO4- , I 2
500-7500
BF4-, ClO4- , I 2
1000
BF4-, ClO4- , I2
1000-10000
AsF5
500
AsF5
10000
AsF5
2700
AsF5, Li, Na
1000
BF4-, ClO4-
50
BF4-, ClO4-
100
HCl
200
H
N
Polipyrol (PPy)
n
S
Politiofen (PTh)
n
S
Poli(3-alkilotiofen)
(PAT)
n
R
Poli(benzenotiol)
S
n
Poli(fenylowinylen)
(PPV)
Poli(tienylowinylen)
(PThV)
n
S
n
Poli(parafenylen)
(PPP)
n
S
Poli(izo-tionaftalen)
n
Polifuran
O
n
Polianilina
(PANI)
N
H
n
Polimery przewodzące (3a)
Zdegenerowny stan podstawowy
E
np.: trans- poliacetylen
Fn
Nie-zdegenerowny stan podstawowy
E
Fn
np.: cis- poliacetylen
forma: trans-cisoid
lub politiofen:
układ chinoidowy
forma: cis-transoid
układ benzoidowy
Polimery przewodzące (4)
Przewodnictwo samoistne
{niestabilność Peierlsa}
Polietylen - dielektryk
hybrydyzacja sp3, pasmo walencyjne całkowicie zapełnione
szerokie pasmo wzbronione
H
H H
H
H
H
H
H
H
H
H
H
EF
H H
C C
H H
s
n
H
H H
H
H
H
H
H
H
H
Poliacetylen - półprzewodnik
wiązania podwójne na przemian z pojedynczymi, hybrydyzacja sp2.
drgania wiązań C-C są przyczyną współistnienia dwóch form:
PRZEWODNIK: syntetyczny metal 1D
w pełni zdelokalizowane elektrony orbitale p
p*
EF
p
rząd wiązania C-C ok. 1,5
pasmo walencyjne zapełnione w połowie
IZOLATOR
zanik sprzężenia wiązań podwójnych, pasmo walencyjne wypełnione całkowicie
p*
1.5eV
p
Polimery przewodzące (5)
Domieszkowanie
polimer silnie
domieszkowany
BIPOLARON
ujemny
S
S
S
S
S
S
S
S
+
k
+
k
+
k
n-domieszkowanie (redukcja)
polimer domieszkowany
POLARON
ujemny
S
S
S
S
S
S
S
S
+
k
+
k
n-domieszkowanie (redukcja)
czysty polimer
S
S
S
S
S
S
S
S
p-domieszkowanie (utlenianie)
Apolimer domieszkowany
POLARON
dodatni
S
S
S
S
S
S
S
S
A-
p-domieszkowanie (utlenianie)
Apolimer silnie
domieszkowany
BIPOLARON
dodatni
S
S
S
S
A-
S
S
S
A-
S
Polimery przewodzące (6)
Hopping
A
B
C
Fibryla
łańcuch polimeru
(A) hopping wewnątrz łańcuchowy
(B) hopping międzyłańcuchowy
(C) hopping międzyfibrylowy
Zjawisko hoppingu jest związane z kwantowym efektem tunelowania nośnika
ładunku przez barierę potencjału.
Bariera potencjał w hoppingu wewnątrz łańcuchowym jest najmniejsza, a w
przypadku hoppingu międzyfibrylarnego największa.
Prawdopodobieństwo tunelowania jest wprost proporcjonalne do temperatury i
odwrotnie proporcjonalne do wysokości bariery potencjału
bariera potencjału
Energia
dostarczamy cząstce dostateczną porcję energii do pokonania bariery
TUNELOWANIE
cząstka nie posiada dostatecznej
energii do przeskoczenia bariery.
zmienna przestrzenna
Polimery przewodzące (7)
Efekt domieszkowania na poziomie molekularnym
Obszar delokalizaji elektronów p
tzw. klaster o właściwościach metalicznych
cząsteczka domieszki
Domieszkowanie polimerów przewodzących powoduje wzrost ich
przewodnictwa z powodu:
¨wprowadzenia dodatkowych nośników ładunku w łańcuchu
polimerowym, (polarony, bipolarony).
¨zwiększenie ruchliwości nośników ładunku poprzez rozszerzenie
obszaru delokalizacji elektronów na sąsiednie łańcuchy
(zmniejszenie bariery potencjału hoppingu)
Polimery przewodzące (8)
Domieszkowanie. Efekt makroskopowy
2
3
przewodnictwo
1
0,01
0,07
0,05
0,03
ułamek molowy domieszki
1 Tzw. obszar przewodnictwa spinowego. Szybki prawie liniowy wzrost przewodnictwa ze
stopniem domieszkowania. Powstają polarony, które są obdarzone wolnym spinem.
2 Tzw. obszar przewodnictwa bezspinowego. Przewodnictwo wzrasta nieznacznie ze wzrostem
stopnia domieszkowania. Zachodzą różne procesy uboczne jak rekombinacja polaronów,
dalsze domieszkowane polaronów z utworzeniem bipolaromów. Wolne spiny zanikają.
Tzw. Obszar przewodnictwa metalicznego. Brak wpływu dalszego domieszkowania na
3 przewodnictwo. Stężenie domieszki jest już tak duże, że cała masa polimeru objęta jest
obszarem quazi-delokalizacji elektronów, które zachowują się w sposób zbliżony do gazu
elektronowego.
Reakcje zachdzące w trakcie domieszkowania polimeru przewodzącego [CP] jodem:
–
++
–
++
–
++
3I2 + [CP]
®
2I 3 + [CP]
5I2 + [CP]
®
2I 5 + [CP]
i pentafluorkiem arsenu:
3AsF 5 + [CP]
®
2AsF 6 + [CP]
+ AsF3