2. Koncentracja swobodnych elektronów i dziur

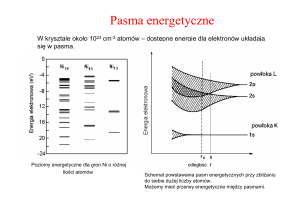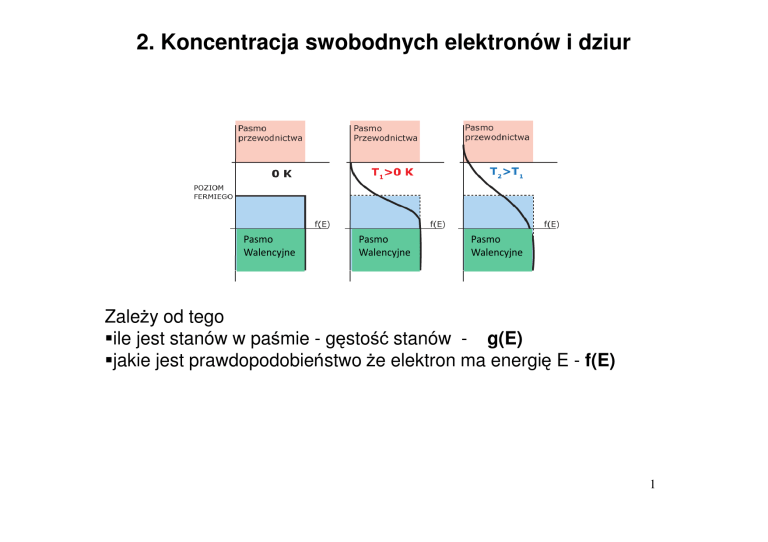
2. Koncentracja swobodnych elektronów i dziur
Pasmo
Walencyjne
Pasmo
Walencyjne
Pasmo
Walencyjne
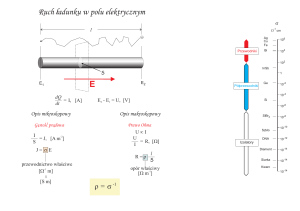
Zależy od tego
ile jest stanów w paśmie - gęstość stanów - g(E)
jakie jest prawdopodobieństwo że elektron ma energię E - f(E)
1
Gęstość stanów w paśmie przewodnictwa i walencyjnym
g(E)
pasmo przewodnictwa: g(E)~(me*)3/2(E-Ec)1/2
pasmo walencyjne: g(E)~(mh*)3/2(EV-E)1/2
Eg
pasmo walencyjne
Ev
pasmo przewodnictwa
EC
energia
Prawdopodobieństwo - rozkład Fermiego-Diraca
T =0K :
fe (E) = 1 dla E < EF
prawdopodobienstwo f(E)
kBT
1.0
T=0
T1>0
fe (E) = 0 dla E >EF
0.5
T2>T1
0.0
EF
energia E
EF- poziom Fermiego, f(EF) = ½
T > 0K
fe (E) =
1
 E −EF 
1+ exp 

 kBT 
2
Koncentracja swobodnych elektronów i dziur
w równowadze termodynamicznej
Pasmo
Walencyjne
T=0 K
brak elektronów w
paśmie przewodn. i
dziur w p. walencyjnym
Pasmo
Walencyjne
Pasmo
Walencyjne
T>0
Im wyższa temperatura, tym większe
prawdopodobieństwo pojawienia się
swobodnego elektronu w pasmie przew.
i dziury w pasmie walencyjnym
3
Koncentracja elektronów w paśmie przewodnictwa
n(E)dE = f e(E)g e(E)dE
∞
n = ∫ n( E )dE
Ec
4
Koncentracja elektronów w paśmie przewodnictwa
(EC-EF)>>kBT
Półprzewodnik niezdegenerowany
fe(E) ≈ exp{-(E-EF)/kBT}
∞
n =
∫ n(E)dE
Ec
∞
=
∫
f e (E)g
e
(E)dE
Ec
 E c − EF 
2(2πme * k B T)3/2
n = Nc exp  −
, gdzie NC =
3
k
T
h
B


Esr = ∫ n( E ) EdE =
3k BT
2
⇓
średnia energia i średnia prędkość elektronu :
vsrel =
3k BT
≈ 106 m / s
me *
5
Koncentracja dziur w paśmie walencyjnym
fh (E) = 1 − fe =
1
 E − EF 
1+ exp  −

 kBT 
(EF-EV)>>kBT
Półprzewodnik niezdegenerowany
fh(E) ≈ exp{-(EF-E)/kBT}
EV
p =
∫
−∞
EV
p(E)dE
=
∫
f h (E)g
h
(E)dE
−∞
 EF − E v 
2(2πm *h k B T)3/2
p = Nv exp  −
, gdzie Nv =
k BT 
h3

6
Półprzewodnik samoistny
Poziom Fermiego w półprzewodniku samoistnym:
n=p
m * 
EF = ½Eg + ¾k B Tln  h  ≈ ½Eg
 m *e 
 E 
np = ni2 = Nc Nv exp− g 
 k BT 
ni - koncentracja nośników samoistnych
np = ni2 zawsze w warunkach równowagi termodynamicznej!
Eg
ni (300 K)
~0.25 eV
1016 cm-3
InSb,PbSe
~1 eV
1010 cm-3
Ge, Si, GaAs
~4 eV
<1010 cm-3
ZnS, SiC, GaN
7
Swobodne elektrony i dziury
Półprzewodnik samoistny
T=0K
T>0K
n=p: poziom EF w srodku przerwy energetycznej
Samoistna koncentracja swobodnych nosników zalezy od T i Eg
 − Eg 
 − Eg 
n = p = ni = N c N v exp 
 ≈ N c ,v exp 

2
k
T
k
T
 B 
 B 
Eg ≅ 1 eV :
ni ≅ 1010 cm-3 ( j = nev=10−12- 10-10 Α/cm2)
8
Domieszkowanie – typ p i n
Przykład - krzem
Sb – donor (5 elektronów walencyjnych)
B – akceptor (3 elektrony walencyjne)
9
Donory i akceptory
poziom donorowy
Ea
poziom akceptorowy
Żeby zjonizować atom domieszki wystarczy bardzo mała energia.
Reprezentujemy ją jako płytki poziom energetyczny
Ed , Ea < 100 meV, zwykle 10-50 meV
10
Typ n
Typ p
Temperatura pokojowa
Ed
EF
++++++++++
swobodne elektrony
zjonizowane donory
EF
Ea
n=Nd
n=Ncexp{-(Ec-EF)/kBT}
Nośniki większościowe
EF blisko krawedzi p. przew
p=ni2/Nd << n
Nośniki mniejszościowe
zjon. akceptory
+ + + + + + + + + swobodne dziury
p=Na
p=NVexp{-(EF-EV)/kBT}
EF blisko krawedzi p. walenc.
n=ni2/Na << p
1 atom na milion zastapiony przez domieszkę
koncentracja nośników wiekszościowych 1016 cm-3 >> ni
koncentracja nośników mniejszościowych 104 cm-3 << ni
11
Koncentracja swobodnych elektronów (dziur)
w funkcji temperatury (półprzewodnik domieszkowany)
niskie T
n lub p =
Nc,vNd,a
exp(−Ed /2k B T)
2
tgα1 =
tgα 2 =
Ed
2k B
Eg
2k B
pośrednie T
n=Nd lub p=Na
wysokie T
Nd<<n, lub Na<<p; EF ≅ Eg/2
nośniki mniejszościowe
typ n:
typ p:
p=ni2/n<<ni n=ni2/p<<ni
12