9.3. Przemiany gazu doskonałego

9. Termodynamika
Podstawowymi pojęciami używanymi w tym dziale fizyki są ciepło i temperatura.
Ciepło jest formą energii wymienianej między układem i otoczeniem w wyniku
istniejącej różnicy temperatur.
9.1. Temperatura
Temperatura jest jedną z podstawowych wielkości w układzie SI i jest mierzona
w kelwinach (K).
Zerowa zasada termodynamiki
Jeżeli ciało A jest w równowadze termodynamicznej z ciałem T (termoskopem)
i ciało B jest w równowadze z ciałem T, wtedy ciała A i B
są w równowadze termodynamicznej ze sobą.
Mówimy, że oba ciała mają tę samą temperaturę.
A
Pomiary temperatury
Definiujemy skalę temperatury. Najbardziej podstawową
jest skala Kelvina ale w praktyce używa się też innych skal (Celsjusza, Fahrenheita).
Aby zdefiniować termometr trzeba wybrać ciało termometryczne, określić cechę
termometryczną i przyjąć określoną zależność między tą cechą i temperaturą,
Wzorcowym termometrem, względem którego są kalibrowane wszystkie inne 1
Termometr gazowy o stałej objętości
Temperaturę T określa się przez pomiar ciśnienia p gazu w stałej objętości.
Wprowadzając liniową skalę temperatury
(9.1)
T  Ap
i biorąc temperaturę punktu potrójnego wody Ttr = 273.16K
jako temperaturę odniesienia, można wyeliminować stałą A
273.16K  A ptr
(9.2)
Dzieląc (9.1) przez (9.2) otrzymuje się
T ( K )  273.16
p
ptr
(9.3)
Ponieważ wskazania takiego termometru zależą od rodzaju
użytego gazu, należy stosować coraz mniejsze ilości gazu
i wyznaczyć temperaturę ekstrapolowaną
p
(9.4)
T ( K )  273.16 lim

p 0
Termometr gazowy
mierzący temperaturę
cieczy
ptr
Wartość ekstrapolowana nazywana jest temperaturą
gazu doskonałego. Termometr gazowy mierzący
temperaturę wrzącej wody. Różne
gazy przy określonym ptr dają różne
temperatury wrzenia ale tylko jedną
wartość ekstrapolowaną 373,125 K.
2
9.2. Ciepło
Ciepło jest formą energii wymienianej między ciałami o różnych temperaturach
(nie jest własnością układu). Podobnie jak praca jest mierzone w dżulach (J).
Uprzednio używano jednostek zwanych kaloriami (1 cal). Związek między ilością
przekazanego ciepła i zmianą temperatury określa ciepło właściwe: jest to ciepło
potrzebne do ogrzania jednostki masy danego ciała o 1 K
Q
(9.5)
c
m T
Powyższa definicja jest bardziej ścisła w formie różniczkowej, a poza tym do
wyznaczenia c ogrzewanie musi następować w ściśle określonych warunkach, np.
przy stałym ciśnieniu lub objętości
 dQ 
c  

m
dT

x
x – stały parametr (p, V,…)
Poniżej podano przykładowe wartości ciepła właściwego w temp. pokojowej
Al
Cu
Pb
woda
rtęć
C[J/g·K]
0.90
0.39
0.13
4.19
0.14
3
9.3. Przemiany gazu doskonałego
Gazy rzeczywiste przy bardzo niskim ciśnieniu są podobne do gazu doskonałego.
(gaz doskonały: punktowe cząstki nie oddziałujące na odległość). Wychodząc z
równania stanu gazu doskonałego
pV  nRT 
m

RT
n – liczba moli, m – masa gazu,
μ – masa 1mola, R –stała gazowa,
łatwo jest wyprowadzić prawa przemian gazu dosk.
1. Przemiana izotermiczna (T = const)
pV  const
2. Przemiana adiabatyczna (Q = 0), brak wymiany
ciepła z otoczeniem

pV  const
κ = Cp/CV
Cp – ciepło właściwe przy stałym ciśnieniu
CV – ciepło właściwe przy stałej objętości
3. Przemiana izochoryczna (V = const)
p  const  T
4. Przemiana izobaryczna (p = const)
V  const  T
A
Przemiany:
izochoryczna 1-3,
izobaryczna 1-2 ,
i izotermiczna 2-3
w układzie p-V
4
9.4. Pierwsza zasada termodynamiki
Zmiana energii wewnętrznej układu ΔU jest równa różnicy między ciepłem do
niego dostarczonym i pracą W wykonaną przez układ
(9.6)
U  Q  W
Jeżeli praca jest wykonywana na układzie, znak „-” w wyrażeniu (9.6) zmieniany
jest na „+”.
Dla każdego z procesów od 1 do 4
przedstawionych na rysunku praca wykonana
przez gaz między stanami A i B stopniowo
maleje (praca objętościowa jest równa polu
pod krzywą p(V)), ciepło dostarczone w
każdym z tych procesów również się zmienia
ale zmiana energii wewnętrznej
U B  U A  Q W jest zawsze taka sama.
Energia wewnętrzna jest funkcją stanu i jej zmiana jest niezależna od drogi
procesu a tylko od położenia stanu końcowego i początkowego.
Dla gazu doskonałego zmiana energii wewnętrznej zależy tylko od zmiany
temperatury U  mc V T
cV – ciepło właściwe przy stałej objętości
5
Przykłady zastosowań I zasady termodynamiki
Jaka jest zmiana energii wewnętrznej w przemianach: adiabatycznej,
izochorycznej i izotermicznej?
a)
Przemiana adiabatyczna, Q = 0.
W tym przyp. wg. I zasady ΔU = Q – W = -W = W’, gdzie W’ – praca wykonana
na układzie (sprężanie gazu powoduje wzrost jego temperatury)
b) Przemiana izochoryczna przebiega w warunkach V = const.
W tym przyp. praca objętościowa W = 0 a zatem ΔU = Q, dostarczone ciepło
powoduje przyrost energii wewnętrznej.
c)
Przemiana izotemiczna przebiega w warunkach T = const.
W tym przyp. ΔU = mCV T = 0 a zatem Q = W, dostarczone ciepło
zamieniane jest na pracę.
6
9.5. Entropia i druga zsada termodynamiki
Procesy, które są zgodne z I zas. termodynamiki nie zawsze są możliwe.
Istnieją procesy, gdzie energia jest zachowana ale są one nieodwracalne, tj. nie może
być zmieniony ich kierunek w wyniku małych zmian otoczenia. Kierunek przebiegu
procesów wskazywany jest przez zmiany entropii: w układzie izolowanym entropia
w procesach nieodwracalnych zawsze rośnie.
Zmianę entropii w procesie odwracalnym można wyznaczyć z relacji
f
S  
i
dQ
T
(9.7)
gdzie i oraz f oznaczają stany początkowy i końcowy, Q jest energią dostarczoną lub
pobraną z układu w temp. T.
Zadanie 1
Wyznaczyć zmianę entropii dla 1 mola azotu w wyniku jego swobodnego rozprężenia
do podwójnej objętości w układzie izolowanym.
Proces swobodnego rozprężania jest nieodwracalny.
Dla swobodnego rozprężania mamy
Q  W  0  U  0  T  const .
W takim przypadku można zamienić ten proces przez odwracalny proces
izotermiczny między tymi samymi stanami początkowym i końcowym i wyznaczyć
7
ΔS z zależności (9.7).
Zmiana entropii w przemianie izotermicznej
f
dQ 1 f
Q
S  
  dQ 
T i
T
i T
Q – ciepło dostarczone do układu
Praca wykonana przez gaz podczas rozprężania
const
nRT
V R – stała gazowa
W   pdV  
dV  
dV  nRT ln f
V
V
Vi n – liczba mli
i
i
i
f
f
f
W przemianie izotermicznej
Q  W ponieważ U  0
Ostatecznie otrzymuje się
S 
Izotermiczne rozprężanie
gazu doskonałego
W nRT Vf
V
J

ln  nR ln f  nR ln 2  1  8,31  ln 2  5,76
T
T
Vi
Vi
K
Ponieważ ΔS jest dodatnie entropia rośnie, czego należało oczekiwać dla
nieodwracalnej przemiany swobodnego rozprężania w układzie zamkniętym.
Analizując proces izotermicznego rozprężania należy brać pod uwagę ciepło, które
jest wymieniane między gazem i otoczeniem (w odróżnieniu od swobodnego
rozprężania, gdzie Q=0) . Dla całego układu zamkniętego gaz – otoczenie całkowita
zmiana entropii jest równa zero, gdyż zmiana entropii otoczenia jest przeciwnego
znaku niż zmiana dla gazu.
8
II zasada termodynamiki
Jest kilka równoważnych sformułowań drugiej zasady . Jedno z nich brzmi:
W procesie, który przebiega w układzie izolowanym, zmiana entropii jest
większa od zera w procesie nieodwracalnym i równa zero w procesie
odwracalnym.
S  0
(9.8)
W świecie rzeczywistym prawie wszystkie procesy są nieodwracalne
i odwracalność jest idealizacją. W organizmach żywych wiele procesów jest
nieodwracalnych ale entropia organizmu nie rośnie ponieważ rośnie entropia
otoczenia.
Cykl Carnota
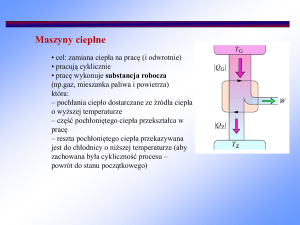
Jest to cykl termodynamiczny, w htórym zamiana ciepła na pracę dokonuje się
A składa się z dwu
z maksymalną sprawnością.
Pełny cykl
procesów izotermicznych AB, CD
Ciepło Q1 jest absorbowane
i dwu procesów adiabatycznych
BC, DA. Dodatnia praca jest
podczas izotrmicznego
wykonywana przez gaz w
rozprężanias AB a Q2 jest
procesach AB i BC. W procesach
CD i DA otoczenie wykonuje
wydalane podczas
pracę na układzie (objętość
izotermicznego sprężania CD. Processes
maleje). Wypadkowa praca W
9 jest
polem
obejmowanym
przez
cykl.
AB i CD są odwracalne.
Cykl Carnota, cd.
Zmiany entropii w procesach składających się na cykl Carnota są następujące.
proces AB: S  B dQ  Q1
(9.9)
1

T
A
T1
S2  0
proces BC:
(9.10)
D
dQ
Q
 2
T
T2
C
S3  
proces CD:
(9.11)
proces DA: S4  0
(9.12)
Całkowita zmiana entropii w pełnym cyklu jest równa zero (entropia jest funkcją
stanu). Z (9.9) – (9.12) otrzymuje się
Q Q
Q T
(9.13)
S  1  2  0  1  1
T1
T2
Q2
T2
Sprawność dowolnego silnika termicznego jest definiowana jako stosunek pracy
wykonanej w cyklu do energii termicznej absorbowanej w tym cyklu
W Q1  Q2
Q
(9.14)
C 

 1 2
Q1
Q1
Q1
Dla silnika Carnota, z użyciem (9.13), otrzymuje się zatem wyrażenie na sprawność
C  1 
T2
T1
Nie istnieją procesy, których jedynym rezultatem jest przepływ ciepła ze zbiornika
ciepła i całkowita zamiana tego ciepła na pracę – równoważne sformułowanie
10
II zasady termodynamiki.
Chłodziarka Carnota
Z użyciem pracy silnik może przenieść ciepło ze źródła o niższej temperaturze do
źródła o wyższej temperaturze. Przykłady: lodówka domowa, klimatyzator, pompa
ciepła. Można to objaśnić na przykładzie odwrotnego cyklu Carnota.
Chłodziarka Carnota
T2  T1
Z (9.13) otrzymuje się
T
Q
i po przekształceniu

1
1
T2
Q2
T1
Q
1  1 1
T2
Q2
co można zapisać jako
T1  T2 Q1  Q2 W


T2
Q2
Q2
A
Współczynnik wydajności chłodniczej chłodziarki Carnota jest więc równy
Q
T
(9.15)
K 

W T T
Przykład:
Jaki jest współczynnik wydajności chłodniczej chłodziarki Carnota pracującej w
przedziale temperatur t2 = -130C, t1 = 270C.
11
T2
260
K
5
Dla
rzeczywistych
chłodziarek
K 

 6,5
2
2
C
1
2
C
9.6. Statystyczna interpretacja entropii
Aby obliczyć zmianę entropii dla swobodnego rozprężania gazu można również
posłużyć się prawami mechaniki statystycznej.
Dokonujemy analizy rozkładu cząsteczek gazu w dwu identycznych połówkach
naczynia. Dla przykładu rozważmy 3 cząsteczki gazu i wyznaczmy liczbę
mikrostanów odpowiadających danej konfiguracji.
konfiguracje
wielokrotność W (liczba mikrostanów)
pierwsza konfiguracja
druga konfiguracja
1
3
Wielokrotność W
konfiguracji jest
liczona ze wzoru
W 
N!
n1 ! n2 !
trzecia konfiguracja
3
gdzie N  n1  n2
czwarta konfiguracja
1
(n! – „n silnia”)
Dla drugiej konfiguracji mamy ze wzoru
W 
3!
6
 3
2!1! 2
12
Statyczna interpretacja entropii, cd.
Różne konfiguracje mają różne liczby mikrostanów, zatem nie są równie
prawdopodobne.
W dyskutowanym przykładzie konfiguracje 2 i 3 są bardziej prawdopodobne niż
1 i 4. Prawdopodobieństwo konfiguracji 2 jest równe 3/8 a konfiguracji 1 jest 1/8.
Przykład
Bierzemy 100 cząsteczek. Jakie są liczby mikrostanów dla konfiguracji:
a) n1 = 100, n2 = 0
Dla dużych N można
b) n1 = 50, n2 = 50
zastosować aproksymację
a)
b)
Stirlinga
W 
N!
100!

1
n1 !n2 ! 100!0!
W 
100!
 1,01  1029
50!50!
ln N! N ln N   N
Najbardziej prawdopodobne są zatem te konfiguracje, gdzie molekuły rozkładają się
po równo w obu połowach naczynia. L. Boltzmann sformułował zależność między
entropią danej konfiguracji i wielokrotnością W tej konfiguracji
S  kB lnW
gdzie
kB  1,38  1023 J kg
jest stałą Boltzmanna.
Ponieważ każdy stan jest równie prawdopodobny, zatem konfiguracje z dużą liczbą
mikrostanów występują najczęściej i odpowiednie entropie przyjmują najwyższe
wartości.
13
Zadanie
Rozwiązujemy ponownie zagadnienie zmiany entropii przy swobodnym
rozprężaniu 1 mola azotu do podwójnej objętości w układzie izolowanym,
wykorzystując reguły statystyki.
W n molach mamy N cząsteczek.
Początkowo (molekuły zjmują lewą połowę zbiornika) wielokrotność konfiguracji
(N,0) jest równa 1.
Gdy molekuły azotu zajmuja pełną objętość, zatem konfiguracja jest (N/2, N/2),
otrzymuje się odpowiednią wielokrotność W  N!
f
Entropia początkowa:
Entropia końcowa:
Si  kB ln1  0
N N
 !   !
2 2
 N  
N  N  N 
Sf  k B lnWf  k B lnN !   2k B ln  !   k B N ln N   N A 2k B  ln    
 2  
2  2 2


N
 k B N lnN   N  N ln   N   k B N lnN   N ln N  ln 2   NkB ln 2
2


Ponieważ NkB = nR otrzymuje się
Sf  nR ln 2
S  Sf  Si  nR ln 2  0  nR ln 2
Otrzymalismy zatem ten sam wynik jak w przypadku gdy zmiana entropii była
14
liczona z przepływu ciepła i zmian temperatury.