Grawitacja
– poziom podstawowy
4
Egzamin maturalny z fizyki i astronomii
Arkusz I
Zadanie
10.pkt)
Wyznaczanie przyspieszenia ziemskiego (2 pkt)
Zadanie
1. (2
CKE 2005 (PP), zad. 23.
do wyznaczenia wartoĞci przyspieszenia Źródło:
Uczniowie przystąpili
grawitacyjnego Ziemi za
pomocą
wahadáa
matematycznego.
10.1 (1 pkt)
Wahadáo odchylono o niewielki kąt od poáoĪenia
równowagi i puszczono. Narysuj siáy dziaáające na
wahadáo matematyczne w tym momencie.
10.2 (1 pkt)
Wahadáo
wprowadzono w ruch. Podaj, jakie wielkoĞci, charakteryzujące wahadáo i jego ruch
wystarczy zmierzyü, aby wyznaczyü wartoĞü przyspieszenia ziemskiego.
Zadanie
11.pkt)
Pole grawitacyjne planety (2 pkt)
Zadanie
2. (2
Źródło: CKE 01.2006 (PP), zad. 11.
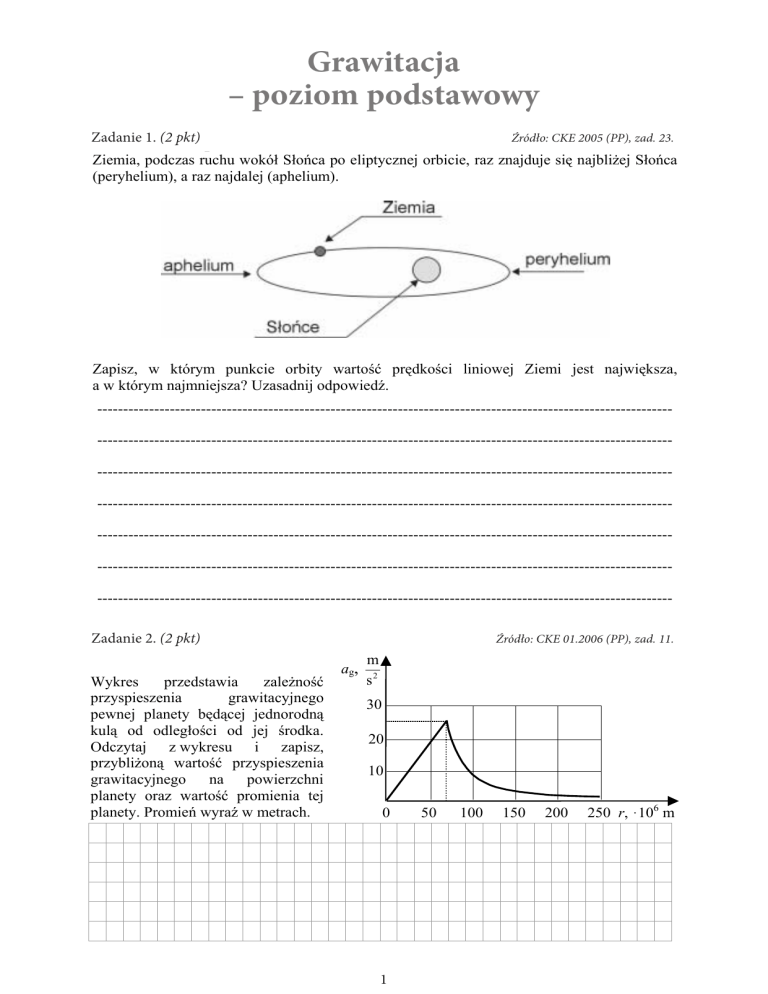
Wykres
przedstawia
zaleĪnoĞü
przyspieszenia
grawitacyjnego
pewnej planety bĊdącej jednorodną
kulą od odlegáoĞci od jej Ğrodka.
Odczytaj z wykresu i zapisz,
przybliĪoną wartoĞü przyspieszenia
grawitacyjnego na powierzchni
planety oraz wartoĞü promienia tej
planety. PromieĔ wyraĨ w metrach.
ag,
m
s2
30
20
10
0
1
50
100
150
200
250 r, ʘ106 m
8
Egzamin maturalny z fizyki i astronomii
Arkusz I
Zadanie
Satelita (2 pkt)
Zadanie 3. 15.
(2 pkt)
Źródło: CKE 05.2006 (PP), zad. 15.
Satelita krąĪy po orbicie koáowej wokóá Ziemi. Podaj, czy nastĊpujące stwierdzenie jest
prawdziwe:
„WartoĞü prĊdkoĞci liniowej tego satelity zmaleje po przeniesieniu go na inną orbitĊ koáową
o wiĊkszym promieniu”.
OdpowiedĨ uzasadnij, odwoáując siĊ do odpowiednich zaleĪnoĞci.
z fizyki i astronomii
Zadanie 16. Pocisk (4 pkt)Egzamin maturalny
Poziom podstawowy
5
Stalowy pocisk, lecący z prĊdkoĞcią o wartoĞci 300 m/s wbiá siĊ w haádĊ piasku i ugrzązá
Zadanie
4. (3
Źródło: CKE 2007 (PP), zad. 14.
w
niej.
14.
Kule
(3 pkt)
pkt)
Dwie maáe jednorodne kule A i B o jednakowych masach umieszczono w odlegáoĞci 10 cm
16.1
(3 pkt)
od siebie. Kule te oddziaáywaáy wówczas siáą grawitacji o wartoĞci 6,67·10-9 N. Obok tych
Oblicz
maksymalny
przyrost
temperatury
jaki wystąpi
w sytuacji
opisanej
w zadaniu
kul umieszczono
maáą
jednorodną
kulĊ C pocisku,
tak, jak pokazano
na rysunku
(widok
z góry).
Masa
przyjmując,
Īe poáowa energii
pocisku
zostaáa zamieniona
przyrost
energii
kuli C jest czterokrotnie
wiĊkszakinetycznej
od masy kuli
B, a odlegáoĞü
pomiĊdzy na
kulą
B i C wynosi
wewnĊtrznej
pocisku. Ciepáo wáaĞciwe Īelaza wynosi 450 J/(kg·K).
20 cm.
A
B
C
Oblicz wartoĞü wypadkowej siáy grawitacji dziaáającej na kulĊ B.
16.2 (1 pkt)
WyjaĞnij krótko, na co zostaáa zuĪyta reszta energii kinetycznej pocisku.
15. Pierwsza prĊdkoĞü kosmiczna (2 pkt)
WykaĪ (nie obliczając wartoĞci liczbowych), Īe wartoĞü pierwszej prĊdkoĞci kosmicznej dla
Ziemi moĪna obliczyü z zaleĪnoĞci v
g RZ gdzie: g – wartoĞü przyspieszenia ziemskiego
na powierzchni Ziemi, a RZ – promieĔ Ziemi.
2
Zadanie
5. (2 pkt)
15. Pierwsza
prĊdkoĞü kosmiczna (2 pkt)
Źródło: CKE 2007 (PP), zad. 15.
WykaĪ (nie obliczając wartoĞci liczbowych), Īe wartoĞü pierwszej prĊdkoĞci kosmicznej dla
Ziemi moĪna obliczyü z zaleĪnoĞci v
g RZ gdzie: g – wartoĞü przyspieszenia ziemskiego
na powierzchni Ziemi, a RZ – promieĔ Ziemi.
6
Egzamin maturalny z fizyki i astronomii
Nr zadania
11
12
13
podstawowy
Wypeánia Maks. liczbaPoziom
pkt
2
2
3
egzaminator!
Uzyskana
liczba
pkt
Zadanie
(4 pkt)
pkt)
16.
Mars6.(4
14
3
15
2
Źródło: CKE 2007 (PP), zad. 16.
Planuje siĊ, Īe do 2020 roku zostanie zaáoĪona na powierzchni Marsa baza dla kosmonautów.
WiĊkszoĞü czasu podczas lotu na Marsa statek kosmiczny bĊdzie podróĪowaá z wyáączonymi
silnikami napĊdowymi.
Zadanie
(2 pkt)
16.1.
(26.1
pkt)
Ustal, czy podczas lotu na Marsa (z wyáączonymi silnikami) kosmonauci bĊdą przebywali
w stanie niewaĪkoĞci. OdpowiedĨ krótko uzasadnij, odwoáując siĊ do praw fizyki.
Wokóá Marsa krąĪą dwa ksiĊĪyce Fobos (Groza) i Dejmos (Strach). Obiegają one planetĊ po
prawie koáowych orbitach poáoĪonych w páaszczyĨnie jej równika. W tabeli poniĪej podano
podstawowe informacje dotyczące ksiĊĪyców Marsa.
Fobos
ĝrednia odlegáoĞü od Marsa
w tys. km
9,4
Okres obiegu
w dniach
0,32
ĝrednica
w km
27
Masa
w 1020 kg
0,0001
GĊstoĞü
w kg/m3
2200
Dejmos
23,5
1,26
13
0,00002
1700
KsiĊĪyc
Na podstawie: "Atlas Ukáadu Sáonecznego NASA", PrószyĔski i S-ka, Warszawa 1999 r.
16.2. (2 pkt)
WykaĪ, korzystając z danych w tabeli i wykonując niezbĊdne obliczenia, Īe dla ksiĊĪyców
Marsa speánione jest III prawo Keplera.
3
Fobos
9,4
Dejmos
23,5
Egzamin maturalny z fizyki i astronomii
0,32
27
Poziom podstawowy
1,26
13
0,0001
2200
0,00002
1700
Zadanie
5."Atlas
(1 pkt)
Na podstawie:
Ukáadu Sáonecznego NASA", PrószyĔski i S-ka, Warszawa 1999 r.
3
Unoszenie siĊ w górĊ iskier nad páonącym ogniskiem w bezwietrzny dzieĔ jest spowodowane
Zadanie
(2 pkt)
zjawiskiem
16.2. (26.2
pkt)
WykaĪ, korzystając z danych w tabeli i wykonując niezbĊdne obliczenia, Īe dla ksiĊĪyców
A. dyfuzji.
Marsa speánione jest III prawo Keplera.
B. konwekcji.
C. przewodnictwa.
D. promieniowania.
Zadanie 6. (1 pkt)
Egzamin
maturalny
z fizyki ipierwszej
astronomii na drugą, to promieĔ orbity
2
Gdy
w atomie wodoru elektron
przejdzie
z orbity
poziom podstawowy
wzrasta czterokrotnie. WartoĞü siáy przyciągania elektrostatycznego dziaáającej pomiĊdzy
jądrem i elektronem zmaleje w tej sytuacji
Zadania zamkniĊte
A. 2 razy.
W zadaniach
od 1. do 10. wybierz i zaznacz jedną poprawną odpowiedĨ.
B. 4 razy.
Zadanie
(1 pkt)
C. 1.
8 razy.
Po przelocie
samolotu powstaje smuga kondensacyjna spalin, tworząc na niebie Ğlad
D. 16 razy.
(rysunek). ĝlad ten przedstawia
Zadanie 7. (1 pkt)
A. cyklotronie
tor.
W
do zakrzywiania torów naáadowanych cząstek wykorzystuje siĊ
B. drogĊ.
A. staáe pole elektryczne.
C. prĊdkoĞü.
B. staáe pole magnetyczne.
D. przemieszczenie.
C. zmienne pole elektryczne.
D. 2.
zmienne
Zadanie
(1 pkt)pole magnetyczne.
Do
pionowo
zawieszonej nitki przymocowano 3 niewielkie oáowiane
kulki.
Zadanie
7. 8.
(1 pkt)
Źródło:
CKE 2008 (PP), zad. 8.
Zadanie
(1
pkt)
OdlegáoĞü miĊdzy stoáem a pierwszą kulką wynosiáa 10 cm a odlegáoĞci
k3
Ziemia krąĪy wokóá SáoĔca w odlegáoĞci w przybliĪeniu 4 razy wiĊkszej niĪ Merkury.
pomiĊdzy kolejnymi kulkami wynosiáy 30 cm i 50 cm odpowiednio (rysunek).
Korzystając z trzeciego prawa Keplera moĪna ustaliü, Īe okres obiegu Ziemi wokóá SáoĔca
NastĊpnie przeciĊto sznurek ponad kulką k3 i kulki zaczĊáy swobodnie spadaü.
jest w porównaniu z okresem obiegu Merkurego
dáuĪszy okoáo
Czas, po którym pierwsza kulka uderzyáa w stóá w porównaniu z czasem, jaki
k2
2 razy.
upáynąáA.
miĊdzy
uderzeniami kolejnych kulek o powierzchniĊ stoáu jest
B. 4 razy.
A. krótszy niĪ czas miĊdzy upadkiem kulek k2 i k3.
C. 8 razy.
k1
B. najkrótszym z czasów miĊdzy upadkiem kolejnych kulek.
D. 16 razy.
C. najdáuĪszym z czasów miĊdzy upadkiem kolejnych kulek.
D. taki sam
Zadanie
9.jak
(1 czasy
pkt) miĊdzy upadkiem kulek k1 i k2 oraz k2 i k3.
Jądro
izotopu
ulegáo rozpadowi promieniotwórczemu. Powstaáo Źródło:
nowe CKE
jądro
zawierające
Zadanie
8. 3.
(1 pkt)
2010
(PP), zad. 3.
(1wiĊcej
pkt) i o jeden neutron mniej niĪ jądro wyjĞciowe. Przedstawiony
oZadanie
jeden proton
powyĪej
W
satelicie
krąĪącym
po
koáowej
orbicie
na
wysokoĞci
znacznie
mniejszej
od
promienia
opis dotyczy rozpadu
Ziemi, uruchomiony zostaá silnik i wartoĞü prĊdkoĞci wzglĊdem Ziemi wzrosáa do 11,2 km/h.
SatelitaA.
tenalfa.
B.
gamma. siĊ po orbicie eliptycznej wokóá Ziemi.
A. bĊdzie poruszaá
C. beta plus.
B. bĊdzie dalej poruszaá siĊ po tej samej orbicie wokóá Ziemi.
D. beta minus.
C. opuĞci orbitĊ okoáoziemską a nastĊpnie naszą GalaktykĊ.
D. opuĞci orbitĊ
i pozostanie w Ukáadzie Sáonecznym.
Zadanie
10. (1okoáoziemską
pkt)
Przyrząd sáuĪący do uzyskiwania i obserwacji widma promieniowania elektromagnetycznego
Zadanie 4. (1 pkt)
to
60
Jednym z izotopów stosowanych do sterylizacji ĪywnoĞci jest izotop kobaltu 27
Co . Jest to
A. kineskop.
izotop nietrwaáy i ulega samorzutnie przemianie E –. Wskutek tego rozpadu powstaje jądro
B. mikroskop.
pierwiastka,
którego liczba protonów w jądrze wynosi
C. oscyloskop.
A. 26. D. spektroskop.
B. 28.
C. 32.
D. 33.
Zadanie 5. (1 pkt)
W póáprzewodnikach domieszkowych typu n, w stosunku do póáprzewodników samoistnych,
mamy do czynienia z
4
A. niedoborem dziur.
Zadania otwarte
Rozwiązanie zadaĔ o numerach od 11. do 21. naleĪy zapisaü w wyznaczonych miejscach
pod treĞcią zadania.
Zadanie
9. 11.
(5 pkt)
Zadanie
Spadający kamieĔ (5 pkt)
Z wysokoĞci 20 m upuszczono swobodnie maáy kamieĔ.
Źródło: CKE 2010 (PP), zad. 11.
Zadanie
9.111.1
(1 pkt)
Zadanie
(1 pkt)
Uzupeánij/dokoĔcz zdanie:
Zjawisko swobodnego spadku w ziemskim polu grawitacyjnym
wystĊpuje wtedy, gdy
prĊdkoĞü początkowa jest równa zero oraz ..................................................................................
Zadanie
9.211.2
(4 pkt)
Zadanie
(4 pkt)
Wykonaj wykres ilustrujący zaleĪnoĞü wysokoĞci, na jakiej znajduje siĊ kamieĔ, od czasu
spadania. Na wykresie nanieĞ 5 wartoĞci liczbowych wysokoĞci (w przedziale czasu 0–2 s).
Wykonaj niezbĊdne obliczenia.
5