Rozkład materiału w podręcznikach „Fizyka z plusem”
CZĘŚĆ 1
Pomiary i jednostki
Pomiary i jednostki
Siły
Siły działające wzdłuż jednej prostej
Mierzenie sił
Dźwignie i bloczki
Siły powodujące obrót
Ruch
Prędkość
Przyspieszenie
Wykresy położenia
Wykresy prędkości
Siły i ruch
Druga zasada dynamiki
Pierwsza zasada dynamiki
Trzecia zasada dynamiki
Zasada zachowania pędu
Ruchy krzywoliniowe
Siła tarcia
CZĘŚĆ 3
Elektrostatyka
Elektryzowanie ciał
Przewodniki i izolatory
Pole elektrostatyczne
Prąd elektryczny stały
Napięcie elektryczne
Prąd elektryczny
Opór elektryczny, prawo Ohma
Obwody elektryczne
Praca i moc prądu
Magnetyzm i elektromagnetyzm
Magnesy
Elektromagnesy
Silnik elektryczny
Indukcja elektromagnetyczna
Prąd przemienny
s. 3–11 w tej broszurze
CZĘŚĆ 2
Energia
Praca
Energia
Zasada zachowania energii
Moc
Struktura materii
Gazy, ciecze i ciała stałe
Gęstość
Temperatura
Rozszerzalność termiczna
Ciecze i gazy
Ciśnienie
Ciśnienie cieczy
Ciśnienie powietrza
Siła wyporu
Pływanie ciał
Ciepło
Ciepło właściwe
Przekazywanie ciepła
Topnienie i krzepnięcie
Parowanie i skraplanie
Zmiany energii wewnętrznej
CZĘŚĆ 4
Drgania i fale
Ruch zmienny
Drgania
Fale mechaniczne
Dźwięk
Przegląd fal elektromagnetycznych
Optyka
Odbicie światła
Zwierciadła kuliste
Załamanie światła
Soczewki
Przyrządy optyczne
s. 12–23 w tej broszurze
tematy wykraczające poza Podstawę programową
2
Druga zasada dynamiki
i. Jedną
we butelk
o
ik
st
la
p
ieś
tyczne
obie. Zaw
dwie iden
ą. Zakręć
st
u
p
a,
Przygotuj
tr
w
e
a
m
pozost
nego
ą, drugą
ponad jed
d
i
o
śc
w
o
o
g
ij
d
łu
łn
ż
d
wią
nape
rku o
nitki przy
k na sznu
cą
le
o
te
m
u
o
b
p
z
n
z jed ą
ie. Za
każdą
rkę). Tera
obok sieb
tu
p
ły
ce
ia
e
is
(r
w
ę
umkę.
gumk
tak aby
ką samą
aciągnij g
n
ta
ą
k
g
le
te
ru
d
u
b
jąc
ę, a
każdej z
z, trzyma
stą butelk
y ją puścis
zymaj pu
d
tr
g
y
i,
rz
lk
p
te
ą
.
u
ręk
wodą
anie się b
pełnioną
uj zachow
utelką na
b
z
b
Zaobserw
ró
z
o
kę. To sam
nadal gum
Jak uzyskać duże przyspieszenie? Bawiąc się kolejką, bez trudu zauważymy,
że kiedy lokomotywa ciągnie wagoniki, rusza z niewielkim przyspieszeniem. Po
odczepieniu wagoników przyspieszenie lokomotywy jest wyraźnie większe. Zatem
przyspieszenie, z jakim porusza się pociąg, zależy od jego masy.
Podobnie przyspieszenie butelki w doświadczeniu domowym zależało od jej masy.
Pełna butelka rozpędzała się powoli, pusta gwałtownie.
mała masa – DUŻE PRZYSPIESZENIE
DUŻA MASA – małe przyspieszenie
Czasami trzeba przetoczyć samochód z unieruchomionym silnikiem. Jeśli samochód będzie pchać tylko jedna osoba, samochód rozpędzi się bardzo powoli, czyli uzyska małe przyspieszenie. Jeśli pomogą przechodnie, na samochód zadziała
większa siła i rozpędzi się on szybciej. Tym samym uzyska większe przyspieszenie.
mała siła – małe przyspieszenie
DUŻA SIŁA – DUŻE PRZYSPIESZENIE
Stwierdziliśmy, że przyspieszenie zależy zarówno od masy ciała, jak i wartości
siły działającej na to ciało. Oczywiście największe przyspieszenie uzyskamy, gdy
będziemy działać dużą siłą na ciało o niewielkiej masie.
FIZYKA 1. Podręcznik s. 76
3
Zależność przyspieszenia od masy. W tabeli podano wyniki pomiarów przyspieszeń, jakie uzyskały dwa wózki pod działaniem różnych sił.
Siła [N]
Przyspieszenie wózka o masie 2 kg
Przyspieszenie wózka o masie 4 kg
[ sm2 ]
[ sm2 ]
4
8
12
16
2
4
6
8
1
2
3
4
ĆWICZENIE 1. a) Przeanalizuj dane zawarte w tabeli. Jakiej wartości przyspieszenia wózka o masie
2 kg należy się spodziewać, gdy działa na niego siła 20 N?
b) Spróbuj odgadnąć związek między działającą na wózek siłą oraz masą i przyspieszeniem
danego wózka.
Pan Marek jest kierowcą ciężarówki. Zauważył, że im większą masę ma wieziony
przez niego ładunek, tym samochód osiąga mniejsze przyspieszenie, mimo że
naciska pedał gazu jednakowo. Postanowił więc zbadać dokładniej tę zależność.
Patrzył na prędkościomierz i zegarek, zapamiętywał, o ile zmieniała się prędkość
w danym czasie, a następnie obliczał przyspieszenie samochodu obciążanego ładunkami o różnych masach. Zauważył, że jeśli łączna masa samochodu i ładunku
zwiększyła się dwukrotnie, to przyspieszenie zmalało dwukrotnie. Jeśli masa została zwiększona trzykrotnie, to przyspieszenie zmalało trzykrotnie.
masa samochodu = 2000 kg
przyspieszenie = 1 sm2
masa samochodu i ładunku = 4000 kg
przyspieszenie = 0,5 sm2
masa samochodu i ładunku = 8000 kg
przyspieszenie = 0,25 sm2
Po kilku próbach pan Marek stwierdził, że przyspieszenie samochodu z ładunkiem maleje tyle razy, ile razy rośnie jego masa.
Jaki byłby efekt zainstalowania w samochodzie pana Marka drugiego silnika, identycznego z pierwszym? Można wyobrazić sobie, że teraz każdy silnik „pcha” tylko połowę masy samochodu, więc samochód może osiągnąć dwukrotnie większe
przyspieszenie. Przyspieszenie samochodu rośnie tyle razy, ile razy rośnie działająca nań siła. Mówimy, że przyspieszenie samochodu jest proporcjonalne do
działającej nań siły.
ĆWICZENIE 2. Jakie największe przyspieszenie mógłby osiągnąć pusty samochód pana Marka
z dwoma silnikami? Masa samochodu wynosi 2000 kg.
4
FIZYKA 1. Podręcznik s. 77
Druga zasada dynamiki Newtona. Zależność przyspieszenia ciała od działającej nań siły nazywamy drugą zasadą dynamiki. Mówi ona, że jeżeli wypadkowa
siła działająca na ciało jest różna od zera, to ciało porusza się ruchem przyspieszonym, przy czym
przyspieszenie ciała =
wypadkowa siła
.
masa ciała
Po wykorzysta
niu wprowadzonych wcześn
iej oznaczeń
otrzymamy
F
a= m
.
ĆWICZENIE 3. Masa kosmonauty wraz z ekwipunkiem
jest równa 100 kg. Na Księżycu byłby on przyciągany z siłą 162 N. Z jakim przyspieszeniem kosmonauta
spadałby na powierzchnię Księżyca?
Stałe przyspieszenie.
Jeżeli na ciało działa stała siła, jego przyspieszenie jest
stałe. Stałe przyspieszenie oznacza, że ciało porusza się ruchem jednostajnie przyspieszonym. Przykładem takiej sytuacji jest spadanie. Jeżeli pominiemy niewielką
siłę oporu powietrza, jedyną siłą działającą na przykład na spadającą stalową kulkę będzie jej ciężar. Ma on stałą wartość, ponieważ masa kulki się nie zmienia.
Dlatego nie zmienia się też przyspieszenie. Oznacza to, że kulka spada ruchem
jednostajnie przyspieszonym.
Obliczanie siły. Na podstawie drugiej zasady dy-
Wzór na siłę
zapisany za
pomocą symbo
li przyjmie
postać
F = m · a.
namiki możemy obliczyć działającą na ciało siłę,
o ile znamy przyspieszenie i masę tego ciała.
siła = masa · przyspieszenie
Na podstawie równości F = m · a określa się również jednostkę siły, którą jest
niuton.
->
-
m
s2
-
>
>
1 N = 1 kg · 1
Siła ma wartość 1 N, jeżeli ciału o masie 1 kg nadaje przyspieszenie 1 sm2 .
Ciężar.
Pod wpływem siły przyciągania Ziemi ciała spadają z przyspieszeniem
m
równym około 10 s2 . Dlatego ciężar danego ciała obliczamy jako iloczyn jego masy
i przyspieszenia ziemskiego.
ciężar = masa · przyspieszenie ziemskie
Na przykład ciężar książki o masie 0,5 kg ma
wartość
Ciężar ciała
zapisany za
pomocą symbo
li przyjmie
postać
Q = m · g.
ZESZYT
ĆWICZEŃ
str. 54
str. 9 w tej
broszurze
m
Q = 0,5 kg · 10 s2 = 5 N.
FIZYKA 1. Podręcznik s. 78
5
Skoki na bungee. Bungee (wym. bandżi), czyli skoki na elastycznej linie, to
dosyć popularna rozrywka.
Gdy skaczący na przykład z mostu
człowiek spada, uzyskuje dużą prędkość. Gdyby był przywiązany do zwykłej liny, hamowałby bardzo gwałtownie (byłoby widać mocne szarpnięcie liny), bo siła hamująca jego ruch miałaby dużą wartość. Mogłaby ona spowo-
Skoki na bungee są bezpieczną rozrywką, o ile elastyczna lina
jest odpowiednio dobrana.
dować uszkodzenie ciała człowieka.
Elastyczne liny używane do skoków działają siłą, której wartość wzrasta powoli
(wraz z rozciąganiem się liny), dlatego też powoli zmniejszają prędkość skoczka.
Łatwiej to będzie zrozumieć po wykonaniu poniższego doświadczenia.
„Twarda” sprężyna działa dużą siłą
i szybko hamuje ruch kulki.
„Miękka” sprężyna działa małą siłą
i powoli hamuje ruch kulki.
Do gwałtownego hamowania, podobnie jak i do
gwałtownego rozpędzania (czyli do ruchów z dużym opóźnieniem lub przyspieszeniem), potrzebna jest duża siła, co wynika z drugiej zasady dynamiki.
Zwykła lina zachowuje się podobnie jak „twarda”
sprężyna, która już po niewielkim rozciągnięciu
działa dużą siłą na zawieszone na niej ciało. Lina używana do skoków jest elastyczna, zachowuje się jak „miękka” sprężyna, która nawet przy dużym rozciągnięciu działa małą siłą na zawieszone
na niej ciało.
6
CIEKAWOSTKA
Słynne zasady dynamiki odkrył Isaac Newton (wym.
Izaak Niuton), wybitny siedemnastowieczny angielski
uczony. Miał wtedy 23 lata.
W wieku 46 lat został posłem do parlamentu. Popularna anegdota mówi, że w czasie obrad parlamentu zabrał
głos tylko raz. Miał poprosić wówczas o zamknięcie
okien z powodu przeciągu.
FIZYKA 1. Podręcznik s. 79
Pytania kontrolne (str. 112) 1–5
ZADANIA
1. Lina holownicza wytrzymuje działanie siły
o wartości co najwyżej 1000 N (większa siła
powoduje rozerwanie liny). Oblicz maksymalne
przyspieszenie, jakie może osiągnąć samochód
o masie 2000 kg holowany na takiej linie po
poziomej jezdni.
A. 0,2 sm2
B. 0,5 sm2
C. 2 sm2
D. 5 sm2
a) Oblicz przyspieszenie samochodu (w sm2 ).
b) Oblicz siłę ciągu silnika, czyli siłę, dzięki której samochód uzyskuje przyspieszenie.
c) Jakie wartości miałyby przyspieszenie i siła,
o których mowa w punktach a) i b), gdyby
samochód rozpędzał się ruchem jednostajnie
przyspieszonym do prędkości 54 km
w czasie 5 s?
h
2. Samochód o masie 1000 kg porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem 2,5 sm2 . Jaką wartość ma wypadkowa
siła działająca na ten samochód?
6. Startująca rakieta
ma masę 400 t, a jej
silniki działają siłą ciągu
równą 10 000 kN.
A. 400 N B. 2500 N C. 40 N D. 250 N
a) Jaki jest ciężar startującej rakiety?
b) Oblicz wypadkową
siłę działającą na rakietę w chwili startu.
W którą stronę jest
zwrócona?
c) Oblicz przyspieszenie
startującej rakiety.
3. Ciało pod działaniem stałej (różnej od zera)
siły porusza się ruchem:
A.
B.
C.
D.
jednostajnym prostoliniowym
niejednostajnie przyspieszonym
jednostajnie przyspieszonym
nie porusza się wcale
4. Masa startowa rakiety kosmicznej to suma
mas rakiety i paliwa. W trakcie lotu paliwo jest
zużywane, więc całkowita masa, jaką muszą
rozpędzić silniki rakiety, się zmniejsza. Silniki rakiety wytwarzają tzw. siłę ciągu działającą na
rakietę. Jak zmieniłoby się przyspieszenie rakiety, gdyby:
a) siła ciągu silników rakiety wzrosła 2 razy
(przy stałej całkowitej masie rakiety),
b) całkowita masa rakiety (przy niezmienionym ciągu silników) zmalała 5 razy,
c) siła ciągu silników rakiety wzrosła 2 razy,
a jej całkowita masa zmalała 4 razy?
5. Samochód pana Wacława osiąga prędkość
w czasie 3 s od momentu ruszenia. Sa54 km
h
mochód ma ciężar 10 000 N. Zakładamy, że
samochód rozpędza się rudo prędkości 54 km
h
chem jednostajnie przyspieszonym. Dla uproszczenia pomijamy wszelkie opory ruchu.
FIZYKA 1. Podręcznik s. 80
7. Na wykresie pokazano wartość siły wypadkowej sił działających na samochód o masie
1000 kg w kolejnych sekundach ruchu.
a) Jakim ruchem poruszał się samochód
w czasie początkowych 10 sekund ruchu, a jakim od dziesiątej do dwudziestej sekundy?
b) Jaką prędkość wskazywał prędkościomierz
) po dziesięciu sekundach
samochodu (w km
h
ruchu, a jaką po dwudziestu, jeżeli w chwili
?
t = 0 s samochód miał prędkość 0 km
h
7
Na zamieszczonym obok zdjęciu widać pilota, który dzięki katapulcie przeżył wypadek (katapulta to urządzenie służące do
wyrzucania fotela z pilotem w razie niebezpieczeństwa). Ponieważ fotel wraz z pilotem musi się szybko oddalić od uszkodzonego samolotu, fotelowi trzeba nadać
bardzo duże przyspieszenie. W tym celu
odpala się ładunek wybuchowy umieszczony pod fotelem lub uruchamia się na
pewien czas silniki rakietowe przymocowane do fotela. Gdy pilot znajdzie się poza samolotem, fotel oddziela się od lotnika
i uwalnia spadochron.
W trakcie katapultowania na lotnika działa siła wielokrotnie przekraczająca siłę, z jaką
przyciąga go Ziemia (czyli ciężar) – mówimy wtedy o przeciążeniu. Na skutek przeciążenia katapultowany pilot ma wrażenie, że stał się wielokrotnie cięższy. Ma kłopot
z poruszeniem kończynami, głową, a przy większych przeciążeniach uszkodzeniu może ulec jego kręgosłup. Ponadto zaburzone jest krążenie krwi w organizmie pilota.
Jeżeli takie skutki utrzymują się zbyt długo, mogą spowodować utratę przytomności,
a nawet śmierć.
Przykładowo silnik rakietowy jednego z typów katapult może działać na fotel z pilotem
siłą równą około 30 kN. Masa fotela to około 150 kg. Przy założeniu, że silniki katapulty
działają pionowo w górę, siedzący w fotelu pilot o masie 100 kg zostałby wyrzucony
m
razem z nim z przyspieszeniem 110 s2 .
Obliczmy siłę, z jaką fotel działałby na pilota.
siła – ciężar pilota = siła wypadkowa
Skorzystamy z drugiej zasady dynamiki i przyrównamy wypadkową siłę działającą na
pilota do iloczynu jego masy i przyspieszenia, jakie uzyskuje.
siła – ciężar pilota = ma
siła = ciężar pilota + ma = 1000 N + 100 kg · 110
m
s2
= 12 000 N
Jest to więc ogromne przeciążenie – siła działająca na pilota jest 12 razy większa od
jego ciężaru.
1. Wymień siły działające na pilota katapultującego się pionowo w górę. W którą stronę działają
te siły?
2. W tekście podano przykładową wartość siły, z jaką silnik rakietowy może działać na fotel pilota.
Przyjmij, że masa pilota to 80 kg, fotela 150 kg i że fotel został wyrzucony pionowo w górę.
a) Oblicz przyspieszenie, z jakim fotel wraz z pilotem zostaną wyrzuceni w górę.
b) Oblicz siłę, z jaką fotel będzie działał na pilota w tej sytuacji.
8
FIZYKA 1. Podręcznik s. 81
Druga zasada dynamiki
Wiele osób uważa, że im większa jest masa ciała, tym szybciej ciało spada. Jest to prawdą, gdy
nie można pominąć wpływu siły oporu powietrza na ruch tych ciał.
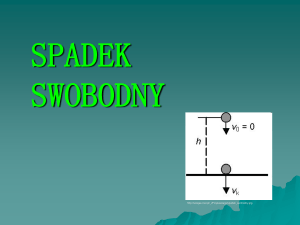
Wyobraźmy sobie, że w powietrzu spadają jednocześnie
trzy kule: stalowa, korkowa i styropianowa, każda o średnicy 10 cm. Jeżeli kule poruszają się z jednakowymi prędkościami, to na każdą z kul działa siła oporu powietrza
o takiej samej wartości. Na przykład przy prędkości 5 ms
siła oporu wynosi 0,05 N. Obok pokazano spadającą stalową kulę i siły na nią działające. Przy rysowaniu wektorów
sił nie zachowano skali, ponieważ siła oporu powietrza jest
niewielka w stosunku do ciężaru kuli.
Uzupełnij tabelę. Przyjmij w obliczeniach przyspieszenie
m
ziemskie równe 9,81 s2 . Wyniki zaokrąglij do dwóch miejsc
po przecinku.
Rodzaj kuli
Ciężar kuli Siła oporu powietrza Siła wypadkowa Masa kuli Przyspieszenie
m kuli
[N]
[N]
[N]
[kg]
s2
stalowa
39,25
korkowa
styropianowa
0,10
0,05
39,20
4,00
0,05
1,13
0,12
0,05
9,80
5,00
Wartość siły oporu powietrza działającej na kule jest taka sama, jednak w porównaniu z wartością ciężaru stalowej kuli jest 785 razy
styropianowej kuli jest 2 razy
.................,
(mniejsza/większa)
a w porównaniu z wartością ciężaru
.. . .. .. .. . .. .. .. ..
(mniejsza/większa)
m
Wartość siły wypadkowej sił działających na stalową kulę, gdy miała ona prędkość 5 s , jest
.................. .................
(niewiele/znacznie)
(mniejsza/większa)
od wartości jej ciężaru. Dlatego kula spada niemal tak, jakby opór
powietrza nie istniał, czyli z przyspieszeniem równym w przybliżeniu przyspieszeniu ziemskiemu.
m
Wartość siły wypadkowej sił działających na styropianową kulę, gdy miała ona prędkość 5 s , jest
................ ................
(niewiele/znacznie) (mniejsza/większa)
od wartości jej ciężaru. Dlatego kula spada z
przyspieszeniem niż wartość przyspieszenia ziemskiego, a więc także
.....................
(mniejszym/większym)
.....................
(mniejszym/większym)
niż war-
tość przyspieszenia stalowej kuli.
FIZYKA 1. Zeszyt ćwiczeń s. 54
9
Druga zasada dynamiki – ZADANIA
1.
Na rysunkach przedstawiono wypadkową siłę działającą na sześcienną kostkę o masie 0,01 kg.
Uzupełnij zdania – skorzystaj z podanej skali i wykonaj odpowiednie obliczenia.
a) Siła o wartości . . . . . . . . . . . . . . . . . nadała kostce na
rysunku A przyspieszenie . . . . . . . . . . . . . . . . . . . .
b) Siła o wartości . . . . . . . . . . . . . . . . . nadała kostce na
rysunku B przyspieszenie . . . . . . . . . . . . . . . . . . . .
c) Kostka na rysunku C porusza się z przyspieszeniem
m
3 s2 . Oznacza to, że działająca na kostkę siła ma wartość . . . . . . . . . . . . . . . . . . Narysuj wektor przedstawiający
tę siłę.
2. W trakcie badań mierzono przyspieszenia uzyskiwane przez ciała pod wpływem działających na
nie sił. Wyniki pomiarów zebrano w tabeli. Jednak niektóre z nich zostały zasłonięte przez kleksy.
Wpisz w miejsca kleksów odpowiednie liczby.
Siła [N]
2
4
4
Masa [kg]
1
1
2
Przyspieszenie
m
s2
2
10
12
2
4
2
4
3. Skorzystaj z danych zamieszczonych w tabeli na stronie 80 i uzupełnij poniższe zdania.
a) Przyspieszenie, z jakim spadają ciała na Ziemi, jest równe
jest równe . . . . . . . . . . . . . . . . . . . . . . . . . , a na Marsie wynosi
................. ........ ,
na Księżycu
................. ........ .
b) Odważnik o masie 10 kg upuszczony na Księżycu spadałby ruchem
.......................................... .
.........................
c) Odważnik o masie 20 kg upuszczony na Księżycu spadałby z przyspieszeniem równym
................. ........ .
10
FIZYKA 1. Zeszyt ćwiczeń s. 55
FIZYKA 1. Zbiór zadań do gimnazjum.
FG1z s. 1
Praca pod redakcją Joanny Gondek
FG1z s. 1
SIŁY I RUCH
1
SIŁY I RUCH
43. Wagonik dziecięcej kolejki elektrycznej pod wpływem siły o wartości 8 N porusza się z przyspieszeniem o wartości 2,5 m2 . Jaką wartość musiałaby mieć siła
s
43. działająca
Wagonik dziecięcej
kolejki
podzwpływem
o wartości
8 N poruna wagonik,
aby elektrycznej
przyspieszenie,
jakim się siły
on porusza,
miało
warm
m
sza się
tość
4,2 z2 ?przyspieszeniem o wartości 2,5 2 . Jaką wartość musiałaby mieć siła
s
s
działająca na wagonik, aby przyspieszenie, z jakim się on porusza, miało warm
tość 4,2 2 ?
ROZWIĄZANIE
1
ZADANIE 42 (s. 40)
s
Sposób I.
ROZWIĄZANIE (s. 91)
ROZWIĄZANIE
Wartość siły F , pod której wpływem ciało o masie m porusza się z przyspieszeniem a,
można
korzystając ze wzoru F = ma.
Sposóbobliczyć,
I.
Wartość
F , pod
której
wpływem
ciałopodana,
o masieale
m można
poruszająsię
z przyspieszeniem
a,
W
treści siły
zadania
masa
wagonika
nie jest
wyznaczyć,
korzystając
obliczyć,
korzystając
ze wzoru
F = ma.
zmożna
informacji
podanych
w pierwszym
zdaniu:
skoro siła o wartości F = 8 N nadaje wagoni1
W treści
zadania masa
wagonika
jest
ale można
ją wyznaczyć,
kowi
przyspieszenie
o wartości
a1 = nie
2,5 sm
, topodana,
masa wagonika
wynosi
m = aF11 = 8 Nkorzystając
m = 3,2 kg.
2
2,5
s2
z informacji podanych w pierwszym zdaniu: skoro siła o wartości F1 = 8 N nadaje wagoniZatem aby wagonik o takiej masie poruszał
się z przyspieszeniem o wartości a2 = 4,2 m2 ,
s
kowi przyspieszenie o wartości a1 = 2,5 sm2 , to masa wagonika wynosi m =maF11 = 8 Nm = 3,2 kg.
2,5 2 N.
siła działająca na niego musiałaby mieć wartość F2 = ma2 = 3,2 kg · 4,2 s2 = 13,44
s
Zatem aby wagonik o takiej masie poruszał się z przyspieszeniem o wartości a2 = 4,2 m2 ,
s
Sposób II.
siła działająca na niego musiałaby mieć wartość F2 = ma2 = 3,2 kg · 4,2 m2 = 13,44 N.
Aby odpowiedzieć na pytanie postawione w zadaniu, obliczenie masy swagonika
nie jest
Sposób II. Na podstawie drugiej zasady dynamiki wiemy, że wartość przyspieszenia ciała
konieczne.
Aby odpowiedzieć
pytanie
postawione
w zadaniu,
obliczenie
masy
wagonika
nie jest
rośnie
tyle razy, ilenarazy
rośnie
wartość siły
działającej
na ciało.
Zatem
aby wartość
m
4,2 2
konieczne. Na podstawie drugiej zasady dynamiki
wiemy, że wartość przyspieszenia ciała
s
przyspieszenia wagonika zwiększyła się aa21 =
m = 1,68 razy, to także siła działająca na
2,5 2
rośnie tyle razy, ile razy rośnie wartość siły
działającej
na ciało. Zatem aby wartość
s
m
wagonik musi mieć 1,68 razy większą wartość,4,2czyli
równą 1,68 · 8 N = 13,44 N.
2
s
przyspieszenia wagonika zwiększyła się aa21 =
m = 1,68 razy, to także siła działająca na
2,5
s2
Odp.wagonik
13,44 Nmusi mieć 1,68 razy większą wartość, czyli równą 1,68 · 8 N = 13,44 N.
Odp. 13,44 N
FIZYKA 1. Zbiór zadań do gimnazjum
11
Ciepło właściwe
Gotowanie wody. Do styropianowego kubka nalano 100 ml wody o temperaturze 20◦ C. Do wody włożono grzałkę o mocy 300 W i jednocześnie włączono stoper,
aby zmierzyć czas, po którym woda się zagotuje. W czasie 1 s grzałka dostarcza
300 J ciepła. Woda zagotowała się po 2 minutach, więc:
dostarczone ciepło = 300 W · 120 s = 36 000 J = 36 kJ.
Następnie zmierzono czas potrzebny do zagotowania 200 ml wody o temperaturze
20◦ C. Woda zagotowała się po 4 minutach, więc:
dostarczone ciepło = 300 W · 240 s = 72 000 J = 72 kJ.
ĆWICZENIE 1. Na podstawie powyższych pomiarów (przy za-
łożeniu, że temperatura początkowa wody wynosi 20 C) oblicz, ile ciepła potrzeba do zagotowania:
a) 0,5 litra wody,
b) 1 litra wody.
1 l = 1000 ml
1 ml = 0,001 l
Aby zagotować wodę, należało zwiększyć jej temperaturę do 100◦ C. Woda, którą
wlewano do kubków, miała temperaturę 20◦ C, a więc trzeba było ją ogrzać o 80◦ C.
Pomiary dokładniejsze od tych, które wykonano, dowodzą, że do zagotowania
wody o masie 1 kg i temperaturze początkowej 20◦ C potrzeba 336 kJ ciepła.
Można również wykazać, że do ogrzania
1 kg wody o każdy kolejny stopień potrzeba
w przybliżeniu jednakowej ilości ciepła. Zatem aby ogrzać 1 kg wody o jeden stopień,
trzeba jej dostarczyć 80 razy mniej ciepła,
czyli 336 kg : 80 = 4,2 kJ.
ĆWICZENIE 2. a) Ile ciepła potrzeba do ogrzania o 10 C wody o masie 1 kg?
b) O ile stopni wzrośnie temperatura wody o masie 1 kg po dostarczeniu jej 84 kJ ciepła?
Również w wypadku innych substancji wzrost temperatury o każdy kolejny stopień wymaga dostarczenia jednakowej ilości ciepła, różnej dla różnych substancji.
Uwaga. Przekazywanie ciepła nie jest jedynym sposobem na ogrzanie ciała. Dowiecie się o tym z tematu „ Zmiany energii wewnętrznej” (str. 125).
Ciepło właściwe. Na wykresach (patrz następna strona) przedstawiono, jak podczas ogrzewania zmienia się temperatura benzyny i wody o jednakowych masach
równych 1 kg. Zwiększenie o 1◦ C temperatury benzyny o masie 1 kg wymaga dostarczenia innej ilości ciepła niż w wypadku wody o takiej samej masie.
12
FIZYKA 2. Podręcznik s. 102
ĆWICZENIE 3. a) Ile ciepła potrzeba do ogrzania o 1 C benzyny o masie 1 kg?
b) Ile razy więcej ciepła potrzeba do ogrzania o 1 C wody o masie 1 kg, w porównaniu z ciepłem
potrzebnym do ogrzania o 1 C benzyny o masie 1 kg?
Aby ogrzać o 1◦ C kilogram danej substancji, trzeba jej dostarczyć określoną ilość
ciepła. Nazywamy ją ciepłem właściwym danej substancji. Wielkość tę oznaczamy
literą c. Jej jednostką jest
J
kg · ◦ C .
CIEKAWOSTKA
Dawniej powszechnie używano innej jednostki ciepła – kalorii, lub jej wielokrotności – kilokalorii. Jedna kaloria (1 cal) to
ciepło potrzebne do ogrzania o 1◦ C wody
Diagram obrazujący wielkość ciepła właściwego różnych
substancji.
o masie 1 g. Jedna kilokaloria (1 kcal) to
ciepło potrzebne do ogrzania o 1◦ C wody
o masie 1 kg (zatem 1 kcal = 4,2 kJ). Obecnie w kilokaloriach podaje się na przykład ilość energii, jaką otrzymuje ludzki
organizm po spożyciu danego produktu
żywnościowego.
Aby zwiększyć temperaturę substancji o dużym cieple właściwym, trzeba jej dostarczyć więcej ciepła niż substancji o takiej samej masie, ale o małym cieple właściwym. Z kolei pewna ilość stygnącej substancji o dużym cieple właściwym oddaje
więcej ciepła niż substancja o takiej samej masie, ale o małym cieple właściwym.
Ciepło z kaloryfera.
Z powodu stosunkowo dużej wartości ciepła właściwego
woda doskonale pełni funkcję substancji chłodzącej (pobierającej ciepło), na przykład w reaktorach jądrowych. Jest również wykorzystywana jako substancja oddająca ciepło, na przykład w kaloryferach.
FIZYKA 2. Podręcznik s. 103
13
ZESZYT
ĆWICZEŃ
str. 68
str. 18 w tej
broszurze
Zastanówmy się, ile ciepła przekazuje kaloryfer
do otoczenia w ciągu jednej godziny. Powiedzmy,
że w tym czasie przez kaloryfer przepływa 5 litrów wody. Każdy kilogram wody, ochładzając się
o 1◦ C, oddaje otoczeniu 4,2 kJ ciepła. Zatem 5 kg
wody oddaje 5 · 4,2 kJ = 21 kJ ciepła. Jeśli woda, przepływając przez kaloryfer, ochładza się
o 20◦ C, to oddaje 20 razy więcej ciepła, czyli
20 · 21 kJ = 420 kJ.
Ciepło pobierane lub oddawane przez daną
ilość substancji obliczamy przez pomnożenie masy tej substancji, jej ciepła właściwego
Po przyjęciu oz
naczeń otrzymujemy
Q = m ·c ·∆t .
i zmiany jej temperatury. Ciepło oznaczamy literą Q , a zmianę temperatury (czyli różnicę między
temperaturą końcową i początkową) – przez ∆t .
ĆWICZENIE 4. Ile ciepła odda w ciągu godziny wo-
da przepływająca przez kaloryfer pokazany na rysunku?
Ciepło właściwe wody wynosi 4,2 kg kJ· C .
Za pomocą grzałki elektrycznej (można ją kupić w sklepach ze sprzętem
AGD) możesz wyznaczyć ciepło właściwe wody. W tym celu należy zmierzyć
ilość ciepła potrzebną do zagotowania określonej masy wody o znanej temperaturze początkowej, a następnie skorzystać z zależności c =
Q
m · ∆t .
Z oprawki grzałki odczytaj jej moc. Włóż 2–3
styropianowe kubki jeden w drugi (aby zmniejszyć odpływ ciepła do otoczenia) i wlej odmierzoną porcję wody (pamiętaj, że 100 ml
wody odpowiada w przybliżeniu 100 g wody). Zmierz temperaturę początkową wody. Jeśli nie masz termometru, wykorzystaj do doświadczenia wodę, która przez kilka godzin
stała w naczyniu w pomieszczeniu o znanej temperaturze powietrza. Możesz wówczas
przyjąć, że temperatura wody jest taka sama
jak temperatura otoczenia. Włóż grzałkę do
wody. Jeszcze jednym kubkiem, ale odwróconym do góry dnem i odpowiednio naciętym,
zasłoń powierzchnię wody (zobacz zdjęcie).
14
FIZYKA 2. Podręcznik s. 104
Pozwoli to na zmniejszenie strat ciepła. Następnie włącz grzałkę i jednocześnie uruchom stoper. Zatrzymaj stoper, gdy woda zacznie wrzeć, czyli gdy
będzie miała 100◦ C.
Przykładowe obliczenia:
moc grzałki P = 300 W
temperatura początkowa 21◦ C
masa wody m = 125 g
temperatura końcowa 100◦ C
czas od włączenia do zagotowania 143 s
różnica temperatur ∆t = 79◦ C
ciepło oddane wodzie przez grzałkę Q = moc grzałki · czas = 300 W · 143 s =
42 900 J
ciepło właściwe c =
Q
42 900 J
kJ
=
≈ 4,3
m · ∆t
0,125 kg · 79◦ C
kg ·◦ C
Różnica pomiędzy zmierzoną wartością ciepła właściwego a podawaną w tablicach fizycznych wynika m.in. ze strat ciepła i niedokładności pomiarów
temperatury oraz czasu.
Wykonaj samodzielnie podobne pomiary, zapisz w zeszycie ich wyniki oraz
obliczenia.
Bilans cieplny.
Do dwóch styropianowych ku-
beczków nalano wody: do jednego 80 ml o temperaturze 26◦ C, a do drugiego 80 ml o temperaturze 40◦ C. Po wymieszaniu wody z obu kubeczków
temperatura wody wynosiła 33◦ C. Cieplejsza woda ochłodziła się więc o 7◦ C, zatem oddane ciepło
było równe:
0,08 kg · 4200
J
kg · ◦ C
· 7◦ C ≈ 2,4 kJ.
Z kolei temperatura chłodniejszej wody wzrosła
o 7◦ C, więc pobrane ciepło było równe:
0,08 kg · 4200
J
kg · ◦ C
· 7◦ C ≈ 2,4 kJ.
Zauważmy, że ciepło pobrane = ciepło oddane. Równość tę nazywamy bilansem
cieplnym. Jest ona szczególnym przypadkiem zasady zachowania energii.
Jednorazowe kubeczki do ciepłych napoi wykonuje się ze styropianu między innymi dlatego, że styropian jest materiałem, który bardzo powoli się nagrzewa.
Dzięki temu straty ciepła (czyli ciepło oddawane otoczeniu) w czasie mieszania
wody ciepłej z zimną są znikome.
Po zmieszaniu jednakowych ilości wody o różnych temperaturach zmiany temperatury każdej z nich były identyczne. Jeżeli jednak masy wody ciepłej i zimnej nie
będą równe, również zmiany ich temperatur nie będą takie same.
FIZYKA 2. Podręcznik s. 105
15
ĆWICZENIE 5. Przyjrzyj się rysunkowi obok.
a) O ile stopni zmieniła się temperatura chłodniejszej
wody, po zmieszaniu wody z obu kubków?
b) Ile ciepła pobrała chłodniejsza woda?
c) Ile ciepła oddała cieplejsza woda?
ZESZYT
ĆWICZEŃ
Doświadczenie
str. 70, 71
str. 20 w tej
broszurze
Na podstawie bilansu cieplnego możemy rówZESZYT
ĆWICZEŃ
Zrób to sam,
str. 72, 73
str. 22 w tej
broszurze
nież ustalić, bez wykonywania pomiarów, końcową temperaturę zmieszanych porcji wody, jeśli
znamy ich masy i temperatury początkowe.
Pytania kontrolne (str. 130) 1–3
ZADANIA
1. Pewną substancję ogrzano o 1 C. Aby
ogrzać o 1 C tę samą substancję, ale o 4 razy
większej masie, potrzeba:
A. tyle samo ciepła
B. 2 razy więcej ciepła
C. 4 razy więcej ciepła
D. 4 razy mniej ciepła
2. Jednostką ciepła właściwego jest:
kg· C
C. JC
D.
A. J
B. J
J
kg· C
3. Temperatura pewnej substancji o masie 5 kg
zwiększyła się o 1 C po dostarczeniu jej 2500 J
ciepła. O ile stopni wzrośnie temperatura 1 kg
tej samej substancji, jeżeli dostarczy się jej
5000 J ciepła?
C. o 2 C
A. o 10 C
D. o 1 C
B. o 5 C
4. Oblicz ciepło właściwe masła, wiedząc,
że temperatura masła o masie 50 g wzrosła
o 10 C po dostarczeniu mu 1025 J ciepła.
5. Mleko sprzedawane w kartonikach ma
przedłużoną trwałość dzięki zastosowaniu tzw.
metody UHT (ang. Ultra High Temperature, czyli bardzo wysoka temperatura). Metoda UHT polega na błyskawicznym (1–2 s)
16
podgrzaniu mleka do temperatury 135–150 C,
a następnie szybkim schłodzeniu do około
20 C. Taki zabieg niszczy mikroorganizmy i nie
zmienia smaku mleka. Ciepło właściwe mleka
wynosi w przybliżeniu 4 kg·kJ C .
Ile ciepła należy odebrać od mleka o masie
2 kg, aby obniżyć jego temperaturę ze 135 C
do 20 C?
6. W tym samym czasie dostarczono tyle samo ciepła do lodu, wody i pary wodnej o jednakowych masach (nie spowodowało to zmiany ich stanów skupienia). Ciepło właściwe lodu
jest równe 2,1 kg·kJ C , wody – 4,2 kg·kJ C , a pary
wodnej – 2 kg·kJ C .
W którym stanie skupienia wody zanotujemy
największy, a w którym najmniejszy wzrost jej
temperatury?
7. Ciepło właściwe soku pomarańczowego jest
równe 3900 kg·J C , a wody wynosi 4200 kg·J C .
Do szklanki, w której znajdowało się 200 g soku o temperaturze 20 C, dolano wodę o masie
50 g i temperaturze 4 C.
Oblicz temperaturę otrzymanego napoju (przyjmij, że nie było strat ciepła). Wynik zaokrąglij
do pełnych stopni.
FIZYKA 2. Podręcznik s. 106
Przypuśćmy, że musimy bardzo szybko przygotować 250 g wody o temperaturze 38◦ C
– na przykład po to, żeby móc jak najszybciej rozrobić mleko w proszku i podać posiłek o odpowiedniej temperaturze płaczącemu niemowlakowi. Co zrobić, aby w jak
najkrótszym czasie uzyskać wodę o określonej temperaturze?
Jednym ze sposobów jest zmieszanie dwóch porcji wody o odpowiednio dobranych masach i znanych temperaturach. Jedną z tych dwóch porcji może być na przykład woda
o temperaturze pokojowej (czyli w przybliżeniu 20◦ C), a drugą – wrzątek. Następnie
trzeba wyznaczyć masę każdej z porcji wody na podstawie bilansu cieplnego.
Przyjmijmy oznaczenia: tp – temperatura pokojowa, mp – masa wody o temperaturze
pokojowej, tw – temperatura wrzątku, mw – masa wrzątku, m – masa wody o temperaturze końcowej, tk – temperatura końcowa, c – ciepło właściwe wody.
Zgodnie z bilansem cieplnym po zmieszaniu obu porcji
wody ciepło oddane przez cieplejszą wodę jest równe
ciepłu pobranemu przez zimniejszą wodę:
mp · c · (tk − tp ) = mw · c · (tw − tk )
mp
mp
· (38◦ C − 20◦ C)
· 18◦ C
mp =
= mw
= mw · 62◦ C
62
18 mw
=
|:c
· (100◦ C − 38◦ C)
31
9 mw
Ponieważ mp + mw = m, więc po podstawieniu do tej
równości wyznaczonej masy mp i znanej wartości m
otrzymamy:
31
9 mw
40
9 mw
+ mw = 250 g
= 250 g
mw ≈ 56 g
mp =
31
9 mw
≈ 194 g
Zatem wystarczy wcześniej przygotować w butelce
około 194 g wody (czyli 194 ml) i odstawić ją, aby uzyskała temperaturę pokojową. Gdy zaistnieje potrzeba,
trzeba będzie tylko zagotować niewielką ilość wody
i dolać tyle wrzątku do wody w butelce, aby było jej
łącznie 250 g (czyli 250 ml). Po wymieszaniu wody jej
temperatura będzie wynosiła około 38◦ C.
1. Ile gramów wody o temperaturze 20 C i ile – o temperaturze 100 C należałoby zmieszać, aby
uzyskać 180 g wody o temperaturze 60 C?
2. Nalejcie wody do butelki i zostawcie ją na jakiś czas w klasie. Potem zmierzcie temperaturę
wody lub temperaturę powietrza w klasie. Obliczcie, ile wody o tej temperaturze i ile wrzątku
trzeba zmieszać, aby otrzymać 250 g wody o temperaturze 38 C. Przeprowadźcie eksperyment
i porównajcie otrzymane wyniki z obliczeniami.
FIZYKA 2. Podręcznik s. 107
17
Ciepło właściwe
Dostarczenie 640 J ciepła pewnej substancji o masie 5 kg powoduje wzrost jej temperatury o 1◦ C.
a) Na podstawie tej informacji uzupełnij tabelę.
Zmiana temperatury [◦ C]
1,0
Dostarczone ciepło [J]
640
2,0
3,0
4,0
5,0
b) Dane z tabeli nanieś na poniższy arkusz i otrzymane punkty połącz linią.
c) Aby ogrzać 5 kg tej substancji o 1◦ C, trzeba jej dostarczyć 640 J ciepła. Oznacza to, że zwiększenie temperatury 1 kg tej substancji o 1◦ C wymaga dostarczenia . . . . . . . . . . . . . . . . . . . . . . . . . ciepła.
Ciepło właściwe tej substancji jest więc równe . . . . . . . . . . . . . . . . . . . . . . . . . . Na podstawie tabeli
zamieszczonej na str. 96 można przypuszczać, że substancją tą jest . . . . . . . . . . . . . . . . . .
d) Na powyższym arkuszu zaznaczono zmiany temperatury 5 kg drugiej ogrzewanej substancji.
Aby ogrzać 5 kg tej substancji o 1◦ C, trzeba jej dostarczyć . . . . . . . . . . . . . . . . . . . . . . . . . ciepła.
Jej ciepło właściwe ma zatem wartość . . . . . . . . . . . . . . . . . . . . . . . . . . Substancją tą może być
......................... .
18
FIZYKA 2. Zeszyt ćwiczeń s. 68
Ciepło właściwe – ZADANIA
1.
Poniżej przedstawiono zmiany temperatur substancji X oraz Y o masie 2 kg każda w zależności
od dostarczonego ciepła.
a) Do ogrzania o 1◦ C substancji X o masie 2 kg potrzeba . . . . . . . . . . . . . . . . .
właściwe tej substancji wynosi więc . . . . . . . . . . . . . . . . . . . . . . . . . .
b) Ciepło właściwe substancji Y jest
........................
(większe, mniejsze)
........
ciepła. Ciepło
od ciepła właściwego substancji X.
c) Aby 5 kg substancji X ogrzać o 20◦ C, trzeba jej dostarczyć
................... ........
ciepła.
2. Wpływająca do kaloryfera woda ma temperaturę 85◦ C, a wypływająca – 65◦ C. W ciągu godziny
przepływa przez kaloryfer 2,5 kg wody.
a) Temperatura wody przepływającej przez kaloryfer maleje o
................. ........ .
b) Woda o masie 1 kg przepływająca przez kaloryfer oddaje otoczeniu
c) Woda przepływająca przez kaloryfer w ciągu godziny oddaje
............
......
................. ........
ciepła.
ciepła.
3. Do garnka zawierającego 0,2 kg wody o temperaturze 50◦ C dolano jeszcze 0,1 kg wody o tem-
peraturze 20◦ C. Po wymieszaniu woda miała temperaturę 40◦ C.
a) Temperatura wody, która na początku była w garnku,
........................
(wzrosła, zmalała)
o
........ ......
.
b) Ile ciepła oddała ciepła woda?
...........................................................................................................
c) Ile ciepła pobrała zimna woda?
...........................................................................................................
FIZYKA 2. Zeszyt ćwiczeń s. 69
19
Doświadczenie
BILANS CIEPLNY
Potrzebne materiały
dwa styropianowe kubki, termometr, menzurka lub waga, kalkulator, czajnik elektryczny
Co trzeba zrobić
a) Nalej do menzurki 100 ml (lub odważ 100 g) zimnej wody z kranu. Przelej ją następnie do
styropianowego kubka.
b) Zmierz temperaturę zimnej wody. Wynik wpisz w odpowiednim miejscu na rysunku A .
c) To samo zrób z ciepłą wodą z kranu albo z wodą zagrzaną w czajniku.
d) Wlej ciepłą wodę do zimnej i lekko zamieszawszy termometrem, zmierz temperaturę mieszaniny.
Wynik pomiaru wpisz na rysunku A .
e) Wykonaj obliczenia i wypełnij pozostałe puste miejsca na rysunku A . Pamiętaj, że ciepło właściwe wody jest równe 4,2 kg kJ· ◦ C .
20
FIZYKA 2. Zeszyt ćwiczeń s. 70
Doświadczenie – BILANS CIEPLNY
f) Wykonaj podobne czynności dla różnych objętości wody ciepłej i zimnej i uzupełnij puste miejsca
na rysunkach.
g) Porównaj wartości ciepła pobranego przez zimną wodę i ciepła oddanego przez ciepłą wodę.
Wyniki zaokrąglij do jednego miejsca po przecinku i wpisz je do tabeli.
Pomiar
Ciepło pobrane [kJ]
Ciepło oddane [kJ]
1
2
3
h) Co może być przyczyną tego, że obliczone ciepło oddane nie jest dokładnie równe obliczonemu
ciepłu pobranemu?
.......................................................................................................
FIZYKA 2. Zeszyt ćwiczeń s. 71
21
Zrób to sam
ILE TRWA ZAGOTOWANIE WODY?
Spróbujmy ocenić, ile co najmniej trwa zagotowanie wody na herbatę na przykład dla twojej
rodziny.
Potrzebne materiały
kilka butelek na wodę, czajnik, zegarek z sekundnikiem, termometr pokojowy, szklanka (przyjmij,
że jej objętość to 250 ml) lub naczynie pozwalające zmierzyć objętość wody (np. mała butelka
o znanej objętości)
Co trzeba zrobić
a) Nalej wodę (łącznie około 3 litrów) do butelek i odstaw je na jakiś czas, tak aby woda miała
temperaturę pokojową.
b) Do czajnika wlej odmierzoną porcję wody, na przykład 200 ml.
c) Jeżeli będziesz używać kuchenki gazowej lub elektrycznej, włącz palnik i odczekaj chwilę, aż się
nagrzeje.
d) Stawiając na palniku czajnik (lub włączając czajnik elektryczny), uruchom równocześnie stoper.
Zmierz czas, po jakim woda się zagotowała. Wynik wpisz do tabeli. Pamiętaj, że woda o objętości
1 litra ma masę około 1 kg.
e) Wylej wodę z czajnika i przepłucz go zimną wodą, aby miał temperaturę pokojową.
f) Wykonaj pomiary dla innych objętości wody, na przykład 0,4 l, 0,5 l, 0,8 l, 1 l.
Masa ogrzewanej wody [kg]
Czas potrzebny do zagotowania wody [s]
22
FIZYKA 2. Zeszyt ćwiczeń s. 72
Zrób to sam – ILE TRWA ZAGOTOWANIE WODY?
g) Uzupełnij oznaczenia osi (symbole wielkości, jednostki, liczby). Następnie nanieś wyniki pomiarów na arkusz.
h) Pomiędzy naniesionymi punktami poprowadź linię prostą, tak aby przechodziła w pobliżu jak
największej liczby punktów. Przedłuż ją do dolnej krawędzi arkusza.
i) Czas potrzebny na ogrzanie pustego czajnika do temperatury 100◦ C, czyli czas pracy palnika
(czajnika) odpowiadający zerowej masie wody jest równy . . . . . . . . . . . . . . . . . . . . . . . . . .
j) Ciepło potrzebne do zagotowania samej wody o masie 1 kg jest dostarczane przez palnik (czajnik)
w czasie . . . . . . . . . . . . . . . . . . . . . . . . . .
k) Temperatura początkowa wody jest równa temperaturze pokojowej i wynosi . . . . . . . . . . . . . . .
Zatem aby zagotować 1 kg wody, trzeba dostarczyć ciepła w ilości
............ ........ · ............ ........ · ............ ........ = ............ ........ .
l) Tego ciepła palnik (czajnik) dostarczył w czasie . . . . . . . . . . . . . . . . .
................. : ................. = ................. ........ .
........ ,
zatem jego moc wynosi
m) Na podstawie wykresu oszacuj, jak długo gotuje się woda na herbatę dla twojej rodziny (przyjmij,
że dla jednej osoby potrzeba 250 ml płynu).
.......................................................................................................
.......................................................................................................
FIZYKA 2. Zeszyt ćwiczeń s. 73
23