Zjawisko rozciągania
i ściskania tkanek,
naprężenia, odkształcenia,
prawo Hook’a
Warszawa, 15 października 2009
Przedmiot wytrzymałości materiałów
• Wytrzymałość materiałów zajmuje się badaniem
sił wewnętrznych w ciałach, aby odpowiedzieć
na pytanie, czy pod wpływem danych obciążeń
w jakimś obszarze ciała siły wewnętrzne nie
osiągną zbyt dużych wartości czy ciało
„wytrzyma” dane obciążenie.
• Drugą,
równie
ważną
dziedziną
badań
wytrzymałości
materiałów
jest
analiza
odkształceń ciał i konstrukcji.
Siły zewnętrzne i wewnętrzne
• Pod nazwą sił zewnętrznych rozumiemy
siły czynne, czyli obciążenia, oraz siły
bierne, czyli reakcje działające z
zewnątrz na dane ciało. Mogą to być
siły skupione, siły powierzchniowe (np.
ciśnienia) lub siły objętościowe (np.
siły przyciągania ziemskiego.
• Siły wewnętrzne to siły z jakimi jedne
cząstki położone wewnątrz ciała
działają na drugie.
Odkształcenia
• Ciała ulegają odkształceniom pod wpływem
działających na nie sił zewnętrznych.
Odkształcenia mogą mieć charakter:
• Sprężysty – po ustąpieniu siły odkształcenia
ustępują, ciało przybiera pierwotną formę,
• Plastyczny – po ustąpieniu siły ciało nie
powraca do pierwotnej formy,
• Niszczące – dochodzi do zniszczenia struktury,
naruszona zostaje spoistość ciała.
Właściwości ciał
• Jeżeli właściwości elementarnej kostki
„wyciętej” z ciała są jednakowe niezależnie od
kierunku, to materiał, z którego zbudowane
jest ciało nazywamy izotropowym
(równokierunkowym) np. metale, plastiki.
• Istnieją również materiały anizotropowe
(różnokierunkowe), to znaczy takie których
właściwości zależą od orientacji względem
płaszczyzn lub kierunków np kierunku słojów
(drewno) kierunku zbrojeń i sposobu ułożenia
warstw (materiały kompozytowe) czy
względem kierunków anatomicznych (kości).
Definicja naprężenia
dF
dS
Jeżeli na nieskończenie małym przekroju dS
wypadkowa sił międzycząsteczkowych wynosi dF,
to iloraz siły dF przez pole dS nazywamy
naprężeniem σ.
Jednostki
• 1N = 1kg·1m/s2
niuton
(jednostka siły)
• 1N·m = 1N·1m
niutonometr
(jednostka momentu siły)
• 1Pa = 1N/m2
paskal
(jednostka naprężenia)
• 1MPa = 1MN/m2= 106N/m2= 1N/mm2
Prawo Hooke’a
• W wyniku obserwacji rozciąganych
prętów pryzmatycznych Robert Hook
(1676) stwierdził, że wydłużenie Δl pręta
pryzmatycznego (pręt – długość jest
znacznie większa od pozostałych
wymiarów poprzecznych) jest wprost
proporcjonalne do siły rozciągającej F i
do długości początkowej l pręta, a
odwrotnie proporcjonalne do pola S
przekroju poprzecznego pręta.
Robert Hooke (1635-1703) – angielski przyrodnik, jeden z
największych eksperymentatorów XVII wieku.
Jest odkrywcą podstawowego
prawa sprężystości (prawo
Hooke'a), wykonał wiele
obserwacji mikroskopowych i
teleskopowych (odkrył m.in.
istnienie gwiazd podwójnych,
Wielkiej Czerwonej Plamy na
Jowiszu), wykonał też szkice
powierzchni Marsa użyte 200 lat
potem do oszacowania szybkości
rotacji tej planety
Prawo Hooke’a
S
l
l
F
Fl
l
ES
gdzie: l – wydłużenie
F – siła,
l – długość początkowa,
E – moduł Younga,
S – pole przekroju poprzecznego
Współczynnik proporcjonalności E – moduł
sprężystości przy rozciąganiu (Moduł Younga, 1807)
l
F
l
S
E
Thomas Young
ur. 1773 w Milverton, zm. 1829 w Londynie
Wyjaśnił mechanizm akomodacji
oka ludzkiego, opisał astygmatyzm
oraz podał teorię widzenia barw
Moduł Younga (E) – inaczej moduł
odkształcalności liniowej albo moduł
sprężystości podłużnej – wielkość
uzależniająca odkształcenie liniowe ε
materiału od naprężenia σ, jakie w
nim występuje w zakresie
odkształceń sprężystych.
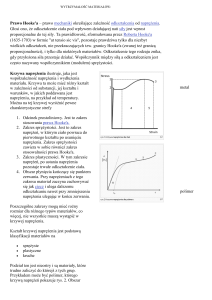
Wykres rozciągania
St3
K
σ
B
C D
L
A
ε
Wykres rozciągania
•
•
•
•
•
•
0A – linia prosta σprop
0B – σspręż
B – granica sprężystości
BD – odkształcenia plastyczne
D – granica plastyczności
K – wytrzymałość na rozciąganie Rm
Wytrzymałość na
• Największe naprężenia, jakie
mogła przenieść badana
próbka, nazywamy
wytrzymałością na
rozciąganie lub
wytrzymałością doraźną
materiału i oznaczamy Rm.
Wytrzymałość na
rozciąganie Rm jest więc
ilorazem maksymalnej siły
Fmax przez pole S przekroju
początkowego próbki.
rozciąganie
Fmax
Rm
S
Naprężenia dopuszczalne
• W celu zabezpieczenia się
przed zniszczeniem
konstrukcji (złamaniem
kości) należy przyjąć pewną
nieprzekraczalną wartość
naprężenia zwaną
naprężeniem
dopuszczalnym kr.
• Obliczone naprężenia
badanego elementu muszą
spełniać warunek:
• nm = współczynnik
bezpieczeństwa dla
rozciągania
F
kr
S
Rm
kr
nm
Wytrzymałość kości
• Właściwości mechaniczne kości i innych
tkanek zależą istotnie od wieku.
• Wytrzymałość kości jest największa w
wieku 30-40 lat, a następnie maleje.
• Wytrzymałość kości jest większa na
ściskanie niż na rozciąganie.
• Wytrzymałość kości na zginanie jest
większa niż na skręcanie.
Wytrzymałość kości udowej
• Średnia wytrzymałość części zbitej
ludzkiej kości udowej u ludzi dorosłych
wynosi:
• Na rozciąganie 107 MPa
• Na ściskanie 139 MPa
• Na zginanie 160 MPa
• Na skręcanie 53 MPa
Wydłużenie graniczne
• Maksymalne wydłużenie względne w
zależności od rodzaju kości wynosi
1,4 - 1,5 %.
• Wraz z wiekiem wartość ta zmniejsza
się co oznacza, że kości osób
starszych są bardziej kruche i mniej
wytrzymałe.
Inne tkanki
• Wytrzymałość mięśni na rozciąganie
0,1-0,3 MPa.
• Wytrzymałość kości gąbczastej na
rozciąganie 1-2 MPa.
• Wytrzymałość chrząstki szklistej 1-40 MPa.
• Wytrzymałość ścięgien 40-100 MPa.