Statyczna próba rozciągania stali Statyczna próba ściskania

ĆWICZENIA LABORATORYJNE
Z MATERIAŁOZNAWSTWA
Statyczna próba
rozciągania stali
Wyznaczanie charakterystyki naprężeniowo – odkształceniowej. Określanie: granicy
sprężystości, plastyczności, wytrzymałości na rozciąganie, naprężenia urywającego
oraz parametrów odkształceniowych.
Statyczna próba ściskania
materiałów kruchych
Wyznaczanie wytrzymałości na ściskanie oraz modułu sprężystości podłużnej
(modułu Younga)
PAWEŁ KAMIŃSKI
[email protected]
SUWMIARKA
Suwmiarką nazywamy przyrząd pomiarowy z noniuszem, używany do pomiaru
wymiarów zewnętrznych, wewnętrznych, a gdy suwmiarka ma wysuwkę
głębokościomierza – również do pomiaru głębokości oraz do pomiaru gwintów.
MATERIAŁOZNAWSTWO vs WYTRZYMAŁOŚĆ MATERIAŁÓW
Wytrzymałość materiałów jest częścią mechaniki o praktycznym,
inżynierskim charakterze.
W rozwiązywaniu konkretnych zadań wykorzystuje się pewne uogólnienia
i uproszczenia. Uproszczenia dotyczą opisu właściwości materiału i opisu
kształtu elementu konstrukcyjnego. Dzięki uproszczeniom rzeczywisty obiekt
zostaje przekształcony w pewien model, który umożliwia rozwiązanie
problemu za pomocą określonego schematu obliczeniowego.
Model (schemat obliczeniowy) musi zachowywać istotne dla
rozwiązywanego problemu cechy i właściwości rzeczywistego obiektu.
UPROSZCZENIA:
- modelu ciała -> ciało jednorodne,
- właściwości materiału -> ciało izotropowe, którego właściwości we wszystkich
kierunkach są identyczne (ciało anizotropowe – różne właściwości), ciało sprężyste
- sposobu rozwiązywania -> uproszczenia inżynierskie.
Statyczna próba rozciągania
W statycznej próbie rozciągania
rozciąga się odpowiednio wykonany
pręt o przekroju okrągłym.
W czasie próby rejestruje się
zależność przyrostu długości próbki
od wielkości siły rozciągającej
Wytrzymałość na rozciąganie
Wytrzymałość na rozciąganie Rm to naprężenie odpowiadające największej sile
rozciągającej F uzyskanej w czasie próby rozciągania, odniesionej do
pierwotnego przekroju poprzecznego tej próbki:
Badanie wytrzymałości na rozciąganie polega na odkształceniu próbki materiału pod wpływem siły
zewnętrznej, działającej w osi próbki.
Próba rozciągania jest podstawowym źródłem informacji o mechanicznych własnościach materiału i
możemy w ten sposób badać wszystkie nie kruche materiały.
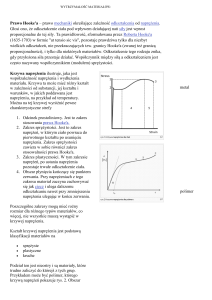
Wykres
Początkowo wzrost naprężenia powoduje liniowy wzrost odkształcenia. W zakresie tym
obowiązuje prawo Hooke'a.
Granica proporcjonalności RH – jest to naprężenie do którego występuje
proporcjonalność naprężenie do wydłużenia jednostkowego (prostoliniowy odcinek
wykresu)
Prawo Hooke'a
• Głosi ono, że odkształcenie ciała pod wpływem działającej na niego siły jest wprost
proporcjonalne do tej siły. Współczynnik między siłą a odkształceniem jest często nazywany
współczynnikiem (modułem) sprężystości.
• Ta prawidłowość, sformułowana przez Roberta Hooke'a (1635-1703) w formie "ut tensio
sic vis", pozostaje prawdziwa tylko dla niezbyt dużych odkształceń, nie przekraczających
tzw. granicy Hooke'a (zwanej też granicą proporcjonalności), i tylko dla niektórych
materiałów. Prawo Hooke'a zakłada też, że odkształcenia ciała, w reakcji na działanie sił,
następują w sposób natychmiastowy i całkowicie znikają, gdy przyłożone siły przestają
działać. Takie uproszczenie jest wystarczające jedynie dla ciał o pomijalnie małej lepkości.
Względne wydłużenie takiego pręta jest wprost proporcjonalne do siły przyłożonej do
pręta, do jego długości i odwrotnie proporcjonalne do pola przekroju poprzecznego
pręta. Współczynnikiem proporcjonalności jest moduł Younga E
gdzie:
F - siła rozciągająca,
S - pole przekroju,
∆l - wydłużenie pręta,
l - długość początkowa.
Moduł Younga (E) – inaczej moduł odkształcalności liniowej albo moduł sprężystości
podłużnej (w układzie jednostek SI) – wielkość określająca sprężystość materiału.
• Wyraża ona, charakterystyczną dla danego materiału, zależność względnego
odkształcenia liniowego ε materiału od naprężenia σ, jakie w nim występuje w zakresie
odkształceń sprężystych.
Przybliżone wartości modułu Younga
dla różnych materiałów
Jednostką modułu Younga jest paskal, czyli
N/m2.
Moduł
Younga
jest
hipotetycznym
naprężeniem,
które
wystąpiłoby
przy
dwukrotnym wydłużeniu próbki materiału,
przy założeniu, że jej przekrój nie ulegnie
zmianie (założenie to spełnione jest dla
hipotetycznego materiału o współczynniku
Poissona υ = 0).
Materiał
Moduł Younga (E)
Guma
Polietylen (LDPE)
Polipropylen (PP)
GPa
0,01–0,10
0,2
1,5–2,0
Żelazo kute i stal
190–210
Poli(tereftalan etylenu)
(PET)
Polistyren (PS)
Nylon
Drewno dębowe
Beton
Magnez (Mg)
3,0–3,5
2–4
11
>27
45
Stop glinu (Al)
69
2,0–2,5
Współczynnik Poissona (ν)
• Jest stosunkiem odkształcenia poprzecznego do odkształcenia podłużnego przy
osiowym stanie naprężenia. Współczynnik Poissona jest wielkością bezwymiarową i nie
określa sprężystości materiału, a jedynie sposób w jaki się on odkształca.
Wykres
Po osiągnięciu naprężenia Rsp, zwanego granicą sprężystości materiał przechodzi w stan
plastyczności, a odkształcenie staje się nieodwracalne. Przekroczenie granicy sprężystości,
zauważalne w okresie chwilowego braku przyrostu naprężenia, powoduje przejście materiału
w stan plastyczny. Dalsze zwiększanie naprężenia powoduje nieliniowy wzrost odkształcenia,
aż do momentu wystąpienia zauważalnego, lokalnego przewężenia zwanego szyjką.
ReL – dolna granica plastyczności
ReH – górna granica plastyczności
Wykres
Naprężenie, w którym pojawia się szyjka, zwane jest wytrzymałością na
rozciąganie Rm. Dalsze rozciąganie próbki powoduje jej zerwanie przy
naprężeniu rozrywającym Ru.
Wydłużenie i przewężenie
Wydłużenie, zdefiniowane zależnością:
A=
Lu − L0
⋅100%
L0
gdzie:
L0 – długość początkowa próbki,
Lu – długość próbki po zerwaniu;
Przewężenie, zdefiniowane zależnością:
A=
A0 − Au
⋅100%
Au
gdzie:
A0 – początkowy przekrój próbki,
Au – przekrój próbki po zerwaniu.
Statyczna próba ściskania, obok statycznej próby rozciągania jest jedną
z podstawowych prób stosowanych dla określenia właściwości mechanicznych
materiałów.
Próba ściskania jest niejako „odwróceniem” próby rozciągania - wykres
ściskania niektórych metali jest symetryczny do wykresu rozciągania w
zakresie ujemnych naprężeń i odkształceń – jego prostoliniowa część jest
niemal równa, co do wielkości tej części przy rozciąganiu.
Typowe charakterystyki naprężenie - odkształcenie uzyskane różnych
typów materiałów.
Badanie wytrzymałości betonu na ściskanie
• Jest to metoda badania betonu, należąca do niszczących. Wytrzymałość betonu na
ściskanie określa się na próbkach sześciennych (fck,cube) lub walcowych (fck,cyl).
• Częstotliwość pobierania próbek nie powinna być mniejsza niż 1 próbka na 100 zarobów,
1 próbka na 50 m3 betonu, 1 próbka na zmianę roboczą i minimum 3 próbki
z danej partii betonu (PN-EN 12350-1:2001).
• Warunki przygotowania próbek do badania i ich pielęgnację określa PN-EN 12390-2:2001,
„Badania betonu. Część 2: Wykonywanie i pielęgnacja próbek do badań
wytrzymałościowych”.
• Wg PN-EN 206-1:2003, „Beton – Część 1: Wymagania, właściwości, produkcja i zgodność”
klasę betonu określa się na podstawie wytrzymałości charakterystycznej betonu na
ściskanie zdefiniowanej jako wartość, poniżej której może znaleźć się nie więcej niż 5%
wyników wszystkich pomiarów wytrzymałości.
PRÓBKA
PRÓBKA
WIELKOŚĆ PRÓBKI
Badanie wytrzymałości betonu na rozciąganie
(PN-G-04302:1997 Skały zwięzłe - Oznaczanie wytrzymałości na rozciąganie metodą poprzecznego ściskania)
Wytrzymałość betonu na rozciąganie zależy w dużej mierze od przyczepności ziaren kruszywa do
stwardniałego zaczynu cementowego. Ze względu na duże zróżnicowanie ziaren kruszywa, wyniki tego typu
badań wykazują duży rozrzut i są zależne od kształtu i wielkości próbek. Z tego względu dla celów praktyki
budowlanej, wytrzymałość na rozciąganie uzależnia się od wytrzymałości na ściskanie.
Badanie wytrzymałości betonu na rozciąganie przy rozłupywaniu nazywane jest często metodą brazylijską.
Wytrzymałość próbek
na rozciąganie przy
rozłupywaniu oblicza
się ze wzorów:
•dla próbek kostkowych
fclspl =2F/πd2
•dla próbek walcowych
fclspl =2F/πdl
ŚCISKANIE JEDNOOSIOWE / ŚCISKANIE TRÓJOSIOWE
STANOWISKO POMIAROWE