Ćwiczenie nr 2 „Wybrane złożone struktury danych” (8.04.2010

Ćwiczenie nr 2
„Wybrane złożone struktury danych” (8.04.2010)
Sprawozdanie wykonali:
Jakub Kliszkowiak (94315)
Jarosław Jankun (94304)
I3
godziny zajęć: czwartek, godz. 11:45
I.
Do wylosowania „n” słów składających się z dziesięciu liter każde, zadeklarowano tablicę
składającą się z tablic dziesięcioelementowych, którym zostają losowo przydzielone kody
ASCII z przedziału <97;122>, a więc są to małe litery alfabetu od a do z.
Rozmiar tablicy zawierającej już wylosowane słowa, ustala użytkownik zaraz po starcie
programu, deklarując dosłownie wartość „n”, czyli liczbę słów.
II.
Po wylosowaniu już tablicy o określonej przez użytkownika liczbie słów (nazwijmy ją tablicą
A), program kopiuje tę tablicę do tablicy pomocniczej (którą z kolei nazwiemy tablicą B)
po czym dokonuje posortowania słów w tablicy B przy użyciu algorytmu sortującego Quick
Sort (oczywiście wg kolejności alfabetycznej). Czas kopiowania elementów z tablicy A
do tablicy B wraz z posortowaniem tej drugiej zostaje zmierzony przy pomocy funkcji
„QueryPerformanceCounter” i „QueryPerformanceFrequency” (w dzisiejszych czasach
dostępe na praktycznie każdym komputerze, mierzą one „tyknięcia” tzw. zegara wysokiej
częstotliwości od czasu startu systemu, a więc jest to metoda bardzo dokładna) po czym
zostaje on wyświetlony w oknie programu.
W kolejnym kroku następuje wyszukiwanie każdego elementu z tablicy A w tablicy
uporządkowanej alfabetycznie B najpierw metodą zwykłą, a następnie metodą dzielenia
połówkowego. Czasy tych procedur zostają zmierzone i przedstawione podobnie jw.
III.
Następnym obiektem badań była lista jednokierunkowa. Stworzona została ona poprzez
wprowadzanie wylosowanych początkowo elementów, w kolejności przed posortowaniem
(tablica A). Podobnie jak wcześniej, wyszukiwane były w liście jednokierunkowej po kolei
elementy z tablicy A. Zarówno czas budowania listy, jak i wyszukiwania w niej elementów
zostały zmierzone i przedstawione użytkownikowi.
IV, V.
Budowa drzewa BST-TR polegała na utworzeniu drzewa decyzji binarnych budując je po kolei
z elementów tablicy A. Drzewo BST-TB zostało zbudowane zaś w oparciu o kolejność
na zasadzie dzielenia połówkowego. Do zmierzenia wysokości obydwu drzew, zostały
wykonane ich kopie, aby nie zaburzyć czasu budowania i wyszukiwania w nich elementów.
Czasy tworzenia obydwu drzew, wyszukiwania w nich kolejnych elementów tablicy A oraz
ich wysokości zostały zmierzone (oddzielnie) i przedstawione.
Pomiary czasu zostały wykonane dla tablic zawierających od 5000 do 50000 słów, ze skokiem
co 5000 (w sumie zostało wykonanych 10 pomiarów). Ich wyniki zostały ręcznie przepisane
do odpowiednich tabeli, na których podstawie sporządzono wykresy. Owe tabele, wykresy
oraz wnioski wyciągnięte z wykonanego doświadczenia przedstawiono poniżej.
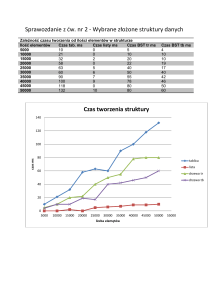
Zależność czasu tworzenia struktur od liczby elementów.
(ms)
TCB
TCL
TCTR
TCTB
5000 10000 15000 20000 25000
30000 35000
40000
45000
50000
6,79 11,08 17,13 23,22 29,78
36,23 42,99
49,25
55,79
63,4
38,45 155,29 354,02 623,44 978,63 1406,45 1925,1 2506,15 3209,69 3945,36
3,06
6,18 10,36 14,06 18,57
22,04 26,21
30,62
35,39
41,68
2,29
4,78
7,34 10,04 12,96
15,55 18,16
21,45
24,27
27,16
70
60
czas (ms)
50
40
Kopiowanie z A do B
30
Tworzenie TR
20
Tworzenie TB
10
0
liczba elementów
4500
4000
czas (ms)
3500
3000
2500
2000
1500
Tworzenie listy
1000
500
0
liczba elementów
Wykres zależności czasu od liczby elementów w przypadku tworzenia listy został przedstawiony
oddzielnie, z racji dużo większych wyników czasowych.
Zależność czasu wyszukiwania od liczby elementów.
5000 10000
15000
20000
25000
30000
35000
40000
45000
50000
105,93 429,51 965,15 1708,71 2677,28 3921,56 5275,71 6885,34 8696,06 10816,21
2,31
5,05
9,26
11,16
14,46
17,72
21,39
24,49
28,44
31,64
120,38 482,89 1086,12 1927,33 3076,8 4350,95 5974,53 7757,67 9849,99 12167,25
2,47
5,42
8,38
11,64
16,13
18,71
22,02
25,62
30,52
35,69
1,86
4,3
6,83
9,17
13,64
14,61
17,68
20,29
23,95
26,61
40
35
czas (ms)
30
25
20
Wyszukiwanie polowkowe
15
Wyszukiwanie w TR
10
Wyszukiwanie w TB
5
0
liczba słów
14000
12000
10000
czas (ms)
(ms)
TsB
TbB
TSL
TSTR
TSTB
8000
6000
Wyszukiwanie normalne
4000
Wyszukiwanie na liscie
2000
0
liczba słów
Wykres zależności czasu od liczby elementów w przypadku tworzenia wyszukiwania normalnego
elementów z tablicy A w tablicy B oraz wyszukiwania tych samych elementów na stworzonej liście
zostały przedstawione oddzielnie, z racji dużo większych wyników czasowych.
Zależność wysokości drzew od liczby elementów.
wysokość 5000 10000 15000 20000 25000 30000 35000 40000 45000 50000
HTR
26
32
34
34
34
35
35
39
40
40
HTB
13
14
14
15
15
15
16
16
16
16
45
40
35
wysokość
30
25
20
Wysokość drzewa TR
15
Wysokość drzewa TB
10
5
0
liczba słów
Eksperyment ten polegał na zbadaniu złożoności kilku struktur danych poprzez wyszukiwanie
w nich elementów. Z goła da się zauważyć, iż dużo korzystniej wyjść można na stworzeniu
z podanej tablicy drzewa decyzji binarnych pomimo iż jego implementacja wymaga
od programisty najwięcej „wysiłku”. Jeżeli dodatkowo pokwapić się o zbudowanie drzewa
wyważonego, czyli takiego do którego elementy dodawać będziemy w kolejności zgodnej
z podziałem połówkowym tablicy n-elementowej, w ów czas otrzymujemy najlepsze wyniki
zarówno czasowo (budowanie jak i wyszukiwanie w nim elementów) jak i w przypadku
wysokości drzewa. Budowa drzewa polega na stworzeniu głównego korzenia (zwanego
również węzłem głównym), który posiada co najwyżej dwójkę dzieci. Każde z dzieci może
również posiadać kolejną dwójkę dzieci itd. Ostatnie z nich, czyli takie od których
nie wychodzą już żadne gałęzie, nazywane są liśćmi.
Efektywność drzewa BST zależy przede wszystkim od jego wysokości. Jeżeliby jako „n”
oznaczyć liczbę elementów (w przypadku tego eksperymentu – liczbę słów dziesięcioliterowych), to w najgorszym przypadku powstanie nam lista jednokierunkowa – ponieważ
każde „dziecko” będzie zawierało tylko jedną gałąź – tak więc czas tworzenia będzie
określony złożonością O(n2), zaś wyszukiwania – O(n). Jest to spowodowane tym,
iż aby znaleźć element znajdujący się w liściu powstałego drzewa, przeszukać trzeba będzie
wszystkie jego elementy.
Drzewo AVL.
Najlepszym przypadkiem drzewa BST jest jego odmiana AVL, a więc drzewko wyważone.
Powstaje ono poprzez wstawianie elementów metodą połówkowego podziału dając tym
samym logarytmiczny czas dostępu (O(log2n)). Czas budowy drzewka AVL opiera
się na złożoności O(n∙log2n). Jest to najkorzystniejsze z możliwych drzew, ponieważ przy jego
budowie osiągana jest najmniejsza (w miarę możliwości) wysokość. W przypadku zwykłego
drzewa BST wysokość ta w najbardziej pesymistycznej wersji (lista jednokierunkowa)
osiągnąć może po prostu n – tyle, z ilu składa się elementów. Jeśli chodzi o drzewo
wyważone, wysokość będzie znacznie mniejsza ponieważ poddrzewa wychodzące z korzenia
będą mniej więcej równe – różnica ich wysokości nie może być większa niż 1. Istnieje również
drzewo dokładnie wyważone – tym razem różnica elementów pomiędzy poddrzewami
wychodzącymi z korzenia może wynosić co najwyżej 1 – takie drzewo jest drzewem o
minimalnej wysokości. Dodatkowo, warto zauważyć, że wysokość tego drzewa wynosić
będzie logn, a liczba elementów na k-tym poziomie równa będzie 2k.
W przypadku przeprowadzanego eksperymentu, jeśli wprowadzalibyśmy elementy z tablicy
posortowanej B do drzewa za pomocą podziału połówkowego otrzymalibyśmy właśnie
drzewko o najmniejszej wysokości – drzewo dokładnie wyważone.
Drzewo BST zawsze jest warto wyważyć, ponieważ jak widzimy na przedstawionych
wykresach, zarówno czas tworzenia jak i czas dostępu do danych w takim drzewku jest
krótszy od zwykłego drzewa BST.
Lista jednokierunkowa a tablica posortowana.
W przypadku listy jednokierunkowej, czas dostępu do danych nie jest zbyt zadowalający.
Zgodnie z powyższymi wykresami, zauważyć możemy iż nie różni się on znacząco od czasu
wyszukiwania elementów w tablicy B. Podobieństwo w czasach wynika z tego, że w obu tych
przypadkach elementy sprawdzane są po kolei – jeden po drugim. Pamiętać jednak musimy,
że tablica B zawiera elementy już posortowane, zaś lista kierunkowa – elementy w kolejności
losowej. Wniosek z tego taki, iż jeśli posiadamy elementy nieposortowane, warto
zaimplementować je do listy jednokierunkowej. Jeśli tablica jest już posortowana – nie ma to
większego sensu.
Porównanie tablicy posortowanej z drzewkiem wyważonym.
Kolejność wprowadzania elementów tablicy B do drzewa AVL oparto, jak już jest wcześniej
wspomniane, na podziale połówkowym. Czasy wyszukiwania połówkowego w tej tablicy,
a wyszukiwania w drzewie wyważonym nie odbiegają znacząco od siebie. Analizujący
ten eksperyment z pewnością zada więc sobie pytanie: po co implementować drzewo decyzji
binarnych, skoro nie daje nam ono dużo lepszych wyników w wyszukiwaniu elementów?
Zauważmy jednak, iż mimo wszystko czas ten jest mniejszy dla drzewa wyważonego,
a różnica ta rośnie wraz ze wzrostem liczby elementów tablicy. Jeżeli więc mamy do
czynienia z niewielką ilością elementów – nie ma sensu implementować drzewa AVL.
Przy większych ilościach zdecydowanie zaleca się włożenie nieco większego wysiłku
i zbudowanie drzewa.
Zajętość pamięciowa poszczególnych struktur.
Podsumowanie.
Przy małej ilości słów najlepszym sposobem na szybkie wyszukiwanie elementów jest
posortowanie ich w tablicy, a następnie wyszukiwanie metodą podziału połówkowego.
Przy większych ilościach warto zasięgnąć po nieco inne struktury danych. Nie ma
sensu budowanie listy jednokierunkowej, jeśli ceni się czas wyszukiwania nad
skomplikowanie implementacji. Istnieje jednak szansa, ze przy budowie drzewa BST
otrzymamy takową listę (w najgorszym przypadku), niepotrzebnie posługując się bardziej
skomplikowaną strukturą danych. Zyskujemy jednak i tak na czasie podczas budowania takiej
listy, a więc mimo wszystko – warto. W przypadku drzewa BST