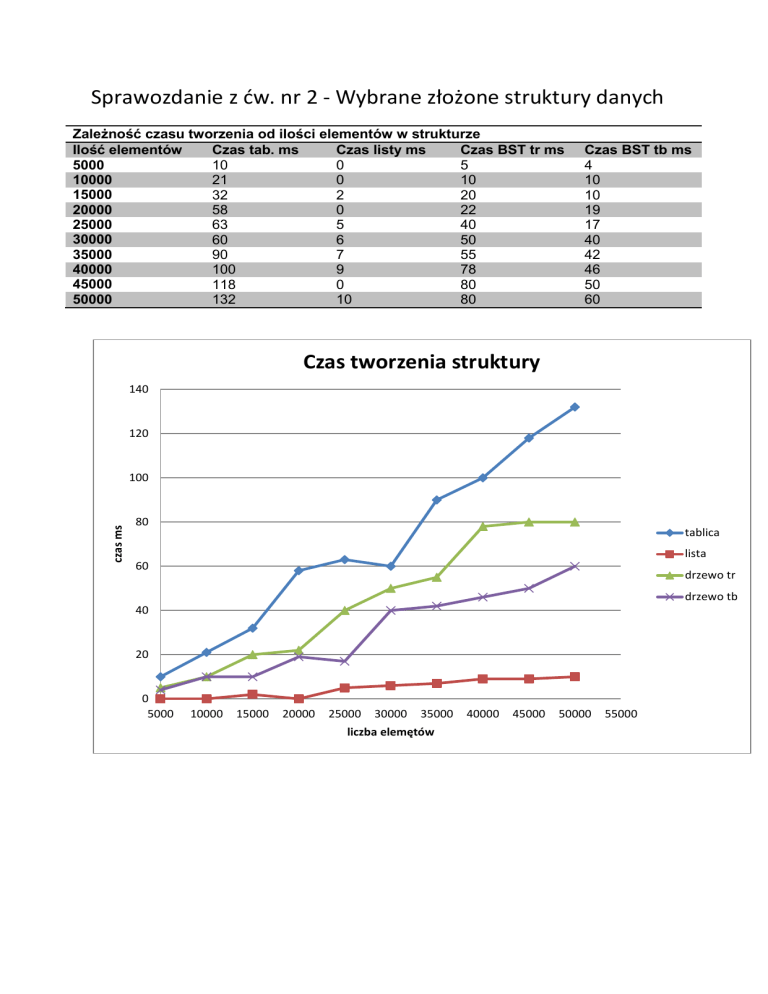
Sprawozdanie z ćw. nr 2 - Wybrane złożone struktury danych
Zależność czasu tworzenia od ilości elementów w strukturze
Ilość elementów
Czas tab. ms
Czas listy ms
Czas BST tr ms
5000
10
0
5
10000
21
0
10
15000
32
2
20
20000
58
0
22
25000
63
5
40
30000
60
6
50
35000
90
7
55
40000
100
9
78
45000
118
0
80
50000
132
10
80
Czas BST tb ms
4
10
10
19
17
40
42
46
50
60
Czas tworzenia struktury
140
120
czas ms
100
80
tablica
lista
60
drzewo tr
drzewo tb
40
20
0
5000
10000
15000
20000
25000
30000
35000
liczba elemętów
40000
45000
50000
55000
Czas wyszukiwania danych w strukturze
Liczba elementów Tablica wycz.
tablica binarne lista
drzewo tr drzewo tb
5000
1516
20
640
8
6
10000
5224
30
2476
20
10
15000
11855
54
5711
30
20
20000
21660
82
10135
40
26
25000
35469
99
16244
54
42
30000
55807
122
23362
70
51
35000
85138
176
34489
100
53
40000
121233
171
41678
112
71
45000
133490
222
52391
110
82
50000
201772
210
62913
110
70
wyszukiwanie w strukturze
1000000
100000
czas ms
10000
tablica
tab bin
1000
lista
drzewo tr
100
drzewo tb
10
1
5000
10000 15000 20000 25000 30000 35000 40000 45000 50000 55000
liczba elementów
Wysokość drzewa binarnego
Liczba elementów
drzewo tr
drzewo tb
5000
25
13
10000
34
14
15000
31
14
20000
35
15
25000
35
15
30000
37
15
35000
37
16
40000
34
16
45000
39
16
50000
36
16
Wysokosc BST
45
40
35
wysokość drzewa
30
25
drzewo tr
20
drzewo tb
15
10
5
0
0
10000
20000
30000
liczba elementów
40000
50000
60000
Wysokość drzewa TR jest znacząco większa od wysokości drzewa TB. Jest to spowodowane
tym, że drzewo nie wywarzone tworzy się z losowo wygenerowanej tablicy A - w związku z
czym możliwe jest każde ułożenie drzewa od najbardziej korzystnego - dokładnie
wywarzonego (liczba elementów w prawym i lewym poddrzewie różni się o co najwyżej 1) z
wysokością rzędu O(log2n) - do najmniej korzystnego - gdy wszystkie elementy będą w jednej
gałęzi, czyli wysokość będzie równa n. Najmniej korzystny przypadek wystąpi, gdy dane będą
posortowane rosnąco albo posortowane malejąco (co wystąpi, kiedy będziemy wprowadzać
dane według tablicy B). Drzewo dokładnie wywarzone uzyskamy, gdy zastosujemy algorytm
dzielenia połówkowego dla posortowanej tablicy.
Powodem różnicy w wysokości między drzewami TR i TB jest inne uporządkowanie
elementów w drzewie. W przypadku drzewa TR uporządkowanie jest losowe i uzyskamy
wysokość rzędu od O(log2n) do O(n). W przypadku drzewa TB elementy są tak
porządkowane, aby wysokość była minimalna, tj. rzędu O(log2n).
Wysokość BST jest znaczącym parametrem tej struktury. Dwa zbiory z identycznymi
elementami mogą stworzyć dwa drzewa różnej wysokości. Z tego względu bardziej korzystne
jest drzewo dokładnie wywarzone, ponieważ jego wysokość może być znacznie mniejsza od
wysokości drzewa nie wyważonego. Czas tworzenia struktury BST jest rzędu O(nlog2n). Czas
wyszukiwania w drzewie jest natomiast rzędu O(h), gdzie h to wysokość drzewa. Jak widać,
wyszukiwanie zdecydowanie zależy od wysokości BST. Tworzenie drzewa dokładnie
wywarzonego będzie się opłacało gdy będziemy chcieli wyszukiwać dane w naszej strukturze.
Wyszukiwanie wyczerpujące w tablicy B i wyszukiwanie na liście wykonują tyle samo
porównań O(n). Można by się więc spodziewać, że czasy wyszukiwania będą takie same,
jednak okazuje się, że istnieje różnica. Czas dostępu do wskaźników i co za tym idzie
kolejnych elementów listy jest trochę mniejszy od dostępu do kolejnych pól tablicy. Dzięki
temu przy dużej ilości elementów różnica w czasie jest spora.
Zarówno w przypadku szukania w drzewie dokładnie wyważonym jak i szukania
połówkowego w tablicy liczba operacji jest taka sama O(log2n). Różnica w czasie wynika, tak
jak w punkcie poprzednim, z różnicy w czasie dostępu do danych.
Największą zajętość pamięciową ma BST, ponieważ musi przechowywać dane o wartości
elementów oraz adresy lewego i prawego poddrzewa. Mniej zajmuje lista - oprócz wartości
elementu przechowuje adres jednego kolejnego elementu. Najmniejszą pod względem
zajętości pamięciowej jest tablica, gdyż przechowuje tylko wartości kolejnych elementów.
Rozmiar pojedynczego elementu tablicy to 14 bajtów(10B ponieważ wartość elementu
stanowi słowo 10 literowe, po jednym bajcie na literę, typ char, 4B ponieważ używamy
stringów które zawierają wskaźniki do tablicy znaków) . Rozmiar elementu listy to 18 bajtów
(14 B - wartość elementu i 4 B - rozmiar wskaźnika do następnego elementu listy), a rozmiar
elementu drzewa to 22 bajtów (14 B - wartość elementu i 8 B - rozmiar wskaźników do
następnych poddrzew) trzeba jednak zauważyć że wskaźnik zajmuje różne ilości pamięci w
zależności od kompilatora.
Drzewo BST ma i wady i zalety. Po pierwsze wymaga najwięcej pamięci z wszystkich tu
omawianych struktur. Jest też najtrudniejsze w implementacji. Nie jest to najlepsza
struktura, jeśli chodzi o usuwanie elementów - najgorszy jest przypadek drzewa
wywarzonego, ponieważ po każdym usunięciu konieczne jest przywrócenie własności
struktury, które są zaburzane. Dodawanie elementów jest prostsze, jednak znalezienie
odpowiedniego miejsca wymaga wielu operacji . W BST, tak jak w liście, nie ma swobodnego
dostępu do każdego elementu. Jednak drzewo ma swoje duże zalety w przypadku
wyszukiwania elementów. Nie musimy szukać wśród wszystkich elementów ale wybieramy
jeden podzbiór, w którym szukamy.
Lista jest strukturą pośrednią między BST a tablicą. Zajmuje mniej miejsca od BST, ale więcej
od tablicy. Jest łatwiejsza w implementacji od BST, ale trudniejsza od tablicy. Jest strukturą
najlepszą pod względem dodawania i usuwania elementów (kolejne elementy dopisywane są
na końcu listy – nie ma więc potrzeby odnajdowania właściwego miejsca; podczas usuwania
elementu należy tylko zmienić wartość wskaźnika poprzedniego elementu listy). Niestety
struktura ta ma najgorszy czas wyszukiwania w niej informacji.
Tablica jest najłatwiejsza w implementacji i zajmuje najmniej pamięci. Wyszukiwanie w niej
informacji na zasadzie połówkowej jest szybsze od szukania w liście, jednak wolniejsze od
BST. Zaletą tablicy jest dostęp swobodny do każdego elementu. Podstawową wadą tablicy
jest to, że w odróżnieniu do listy i drzewa, nie jest to dynamiczna struktura danych. Rozmiar
tablicy trzeba zadeklarować na początku. Tak więc usuwanie i dodawanie elementów jest
utrudnione.