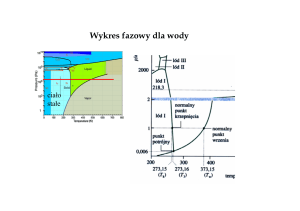
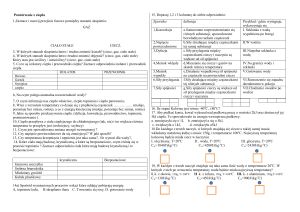
Ciepło właściwe - przypomnienie
1 Q
cV
m T V
dU Q W
1 Q
cp
m T p
d U pV Q
H
1 U
cV
m T V
1 H
cp
m T p
H = U + pV - entalpia
Anomalie występujące na krzywej ciepła właściwego są konsekwencją
zachodzących przemian fazowych.
Z wielkości tych anomalii można znaleźć entropię lub entalpię przemiany.
Eksperymentalnie można wyznaczyć średnią wartość ciepła właściwego w
przedziale temperatury ΔT
ceksp
1 Q
m T
Jak przejść do cp lub cV?
Należy wprowadzić poprawki wynikające z faktu, że pomiary
prowadzone są na próbkach stałych i ciekłych w obecności ich par –
ciepło właściwe przy ciśnieniu par nasyconych badanej substancji cs
W przypadku zdecydowanej większości ciał stałych różnice pomiędzy cs
a cp są pomijalnie małe.
Ciepło właściwe ciał stałych
Brak przemiany
fazowej
Przy obniżaniu temperatury ciepło
molowe
Cp T 3
Ze wzrostem temperatury, dla
atomowych ciał stałych
J
C p 25
mol K
Dla molekularnych ciał stałych
C p 25 100
J
mol K
Reguła Dulonga-Petita
Temperatura Debye’a
aluminum
426 K
platyna
240 K
kadm
186 K
krzem
640 K
chrom
610 K
srebro
225 K
miedź
344,5 K
cyna (biała, β)
195 K
złoto
165 K
tytan
420 K
żelazo
464 K
wolfram
405 K
ołów
96 K
cynk
300 K
magnez
476 K
diament
2200 K
nikiel
440 K
lód
192 K
Przejście fazowe może być przejściem strukturalnym – wiąże się ze
zmianą struktury, lub dynamicznym – zmiana konfiguracji molekuł.
95.6ºC
jednoskośna
Przejście to ma podobny charakter do topnienia
Klasyfikacja przemian fazowych
Podstawą do klasyfikacji różnych typów przemian jest zachowanie się
funkcji termodynamicznych, w tym ciepła właściwego, w okolicy
temperatury przemiany.
Przejścia fazowe I rodzaju
Energia wewnętrzna danej fazy zmienia się w sposób ciągły wraz ze
zmianą parametrów.
Przy przejściu z jednej fazy do drugiej – zmiana struktury
lód
woda
siarka rombowa
jednoskośna
energia wewnętrzna i entalpia zmieniają się w sposób nieciągły.
Oznacza to, że energia wewnętrzna lodu i wody jest inna – np. inne siły
spójności.
Niech przejście fazowe zachodzi przy stałym ciśnieniu w temperaturze
Tp
2
dH H 2 H1 Q p
dH C p dT
1
pojemność cieplna
Ponieważ U i H są nieciągłe, nieciągłe są również
U
,
T V
H
T p
Przejścia, w których dana substancja chemiczna zmienia swą fazę tak, że
U i H (a więc CV i Cp) zmieniają się w sposób nieciągły – przejścia fazowe
I rodzaju.
Zmiana entropii
S
Q
T
w przemianach fazowych I rodzaju jest również nieciągła.
Charakterystyczne cechy przejść fazowych I rodzaju
• możliwość wytworzenia fazy niestabilnej termodynamicznie, np.
przechłodzonej poniżej Tc odmiany wysokotemperaturowej,
• istnienie ciepła utajonego przemiany
• współistnienie w punkcie przemiany dwu różnych faz (np.
mieszanina siarki jednoskośnej i rombowej).
• warunkiem współistnienia różnych faz jest równość entalpii
swobodnych tych faz
G H TS
G – funkcja Gibbsa
GI GII
Ponieważ obydwie fazy są fizycznie rozróżnialne
funkcjami p i T
GI GII
G
GII
GI
Tp
faza I
GI , GII są różnymi
T
faza II
GI
GII
T p T p
G
Faza I może istnieć powyżej temperatury
GII
Faza II może istnieć poniżej temperatury
GI
Tp
faza I
T > Tp
T
faza II
T < Tp
takie stany nazywamy metastabilnymi.
Woda o dużym stopniu czystości schładzana poniżej 0C może pozostać
w stanie ciekłym – ciecz przechłodzona.
Nie jest to stan stabilny – niewielkie zaburzenie powoduje krystalizację
przejście do stanu o minimalnej wartości funkcji Gibbsa.
Podobnie zaobserwujemy przegrzaną ciecz lub przesyconą parę.
GI GII
Przejścia fazowe II rodzaju
GI
GII
T p T p
GI
p
GII
T p
T
C pI C pII
G
S
GI
S II
GII
Tp
SI
T
Tp
T
Przejścia fazowe II rodzaju
Niełatwo jest stwierdzić eksperymentalnie, czy przejście fazowe jest
I czy II rodzaju na podstawie zależności cp(T)
Układ opisany jest tą samą funkcją G(p,T) w fazie I i II. W Tp istnieje
jedna faza – nie ma ciepła utajonego.
Anomalia związana z takim przejściem ma kształt litery λ
Przejście helu I w hel II w temp. 2.2 K
Przejście typu porządek – nieporządek jest przejściem II rodzaju
stop Cu-Zn – faza niskotemperaturowa – każdy atom Cu jest
otoczony przez 8 atomów Zn i każdy atom Zn jest otoczony przez 8
atomów Cu.
W fazie wysokotemperaturowej
struktura tego samego typu –
ale atomy Zn i Cu są
rozmieszczone w sposób
przypadkowy w sieci
krystalicznej – struktura
nieuporządkowana.
Związek ciepła właściwego z dynamiką
kryształów
Jak wyjaśnić kształt zależności ciepła właściwego od temperatury?
Ciepło właściwe jest wielkością makroskopową, zależną od stanów
energetycznych atomów lub cząsteczek tworzących badany układ.
Przejście od stanów mikroskopowych (opisywanych przez mechanikę
kwantową) do ciepła właściwego jest możliwe na gruncie fizyki
statystycznej.
Zmiana stanu energetycznego danego układu związana jest z
istnieniem różnego rodzaju wzbudzeń, wnoszących przyczynki do
pojemności cieplnej.
Najbardziej istotny udział , w szerokim zakresie temperatur, mają
drgania sieci – fonony.
Ponadto – drgania wewnętrzne molekuł, stany elektronowe w metalach,
stany wzbudzone związane z falami spinowymi w magnetykach.
Energia układu jest sumą wszystkich przyczynków.
Udział drgań sieciowych w cieple właściwym
Drgania sieciowe – sprzężone (kolektywne) oscylacje atomów, jonów lub
cząsteczek wokół ich położeń równowagi zajmowanych w węzłach sieci
krystalicznej.
Dla kryształów atomowych, składających się z N atomów istnieje 3N
oscylacyjnych stopni swobody. Każdy atom wykonuje oscylacje w polu
wytworzonym przez sąsiadów
Struktura diamentu
Jeśli energia każdego z atomów nie zależy od ruchu sąsiadów, to cały
kryształ możemy traktować jako układ 3N niezależnych oscylatorów.
Zgodnie z zasadą ekwipartycji energii
U 3RT
U
J
CV
3R 25
T
mol K
W niższych temperaturach istotny jest kwantowy charakter drgań
wykonywanych przez atomy.
Udział drgań sieciowych w cieple właściwym maleje z temperaturą.
Kryształ molekularny
W krysztale molekularnym należy uwzględnić udział drgań
wewnętrznych molekuł w cieple właściwym.
Częstość tych drgań na ogół jest
wysoka ~ 1015 Hz – ich wkład jest
zaniedbywalny przy
temperaturach pokojowych i
niższych. Udział rotacji cząsteczki
jako całości jest znaczny.
temperatura T
Topnienie
Krzywa topnienia ciał
amorficznych – szkieł
ciepło Q
Topnieniu towarzyszy pochłanianie
ciepła bez zmiany temperatury ciała
– ciepło utajone przemiany. Do
stopienia m kg danej substancji
należy dostarczyć
Q mc
ciepła.
Ciepło topnienia
c
Q
m
Jest to ilość ciepła potrzebna do przeprowadzenia 1 kg danego ciała
stałego w ciecz o tej samej temperaturze.
W temperaturze topnienia mamy równowagę termiczną pomiędzy
ciałem stałym a cieczą.
Krzepnięcie i przechłodzenie
Podczas krzepnięcia ciało oddaje ciepło
ciepło krzepnięcia = ciepłu topnienia
Aby krzepnięcie ciała następowało w określonej temperaturze, konieczna
jest obecność centrów krystalizacji – zarodków krystalicznych.
W przypadku braku zarodków – krzepnięcie ulega opóźnieniu, mimo
osiągnięcia temperatury krystalizacji - ciecz przechłodzona.
Czysta (bez zarodków krystalizacji) woda może być przechłodzona do 72C.
Ciała amorficzne łatwo ulegają przechłodzeniu. Lepkość wzrasta tak
silnie, że cząsteczki nie mogą ułożyć się w sieć krystaliczną. Stan cieczy
przechłodzonej jest stanem metastabilnym
Parowanie i skraplanie (kondensacja)
stan ciekły
parowanie
stan gazowy
skraplanie
stan stały
sublimacja
stan gazowy
resublimacja
Parowanie odbywa się w każdej temperaturze na powierzchni cieczy.
Szybkość parowanie rośnie gdy rośnie temperatura, maleje – gdy rośnie
ciśnienie.
Parowanie w całej objętości cieczy – wrzenie.
Temperatura wrzenia zależy od ciśnienia – gdy ciśnienie rośnie –
temperatura wrzenia rośnie.
Temperatura wrzenia wody w funkcji ciśnienia
Przegrzanie cieczy
Ciecz można przegrzać znacznie powyżej temperatury wrzenia, gdy:
• podgrzewamy ciecz bardzo powoli,
• brak jest w cieczy zarodków pary.
• ciecz przegrzana jest w równowadze nietrwałej – łatwo wywołać
wrzenie wybuchowe.
Ciepło parowania
Q
c
m
Jeśli nie ma dopływu ciepła z zewnątrz – ciecz parując odbiera
potrzebne ciepło z samej cieczy – oziębia się.
Podczas kondensacji ciepło jest oddawane – powstająca w wyniku
skraplania ciecz ogrzewa się.
Gęstość pary nasyconej wzrasta z temperaturą
Gęstość cieczy maleje z temperaturą.
Pary nienasycone – przegrzane – zachowują się podobnie jak gazy,
spełniają więc równanie Clapeyrona – odchylenia od równania gazu
doskonałego są większe niż dla innych gazów.
Dla par nasyconych równanie stanu gazu nie jest spełnione.