wspolzaleznosc-zmiennych-losowych-w-procesie

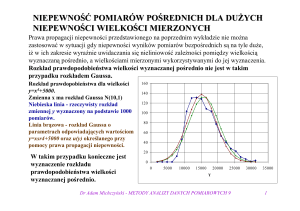
2
Wykład 4
Współzależność zmiennych losowych w procesie symulacji metodami z grupy Monte Carlo
Odzwierciedlenie współzależności jest podstawowym elementem symulacji metodami z gru-py
Monte Carlo. W rzeczywistości gospodarczej większość czynników ryzyka wpływających na
podmioty gospodarcze wykazuje współzależności. Identyfikujemy, między innymi, współ-zależność
zmian kursów walutowych, stóp procentowych, cen towarów i usług, cen akcji, popytu na towary i
usługi. Współzależności mogą mieć różne natężenie i różny kierunek. Najpopularniejszym
sposobem pomiaru natężenia i kierunku współzależności są współczynkorelacji rangowej
Współczynnik korelacji tau Kendall'a oparty na prawdopodobieństwie zmiany. Współczynnik
korelacji liniowej przyjmuje wartości w zakresie od -1 do 1. Wartość współ-czynnika korelacji
liniowej Pearson'a powyżej |0,9| uznawana jest za symptom silnej współ-zależności. Wartość
współczynnika poniżej |0,9| a powyżej |0,6| jest uznawana za symptom średniej współzależności,
dodatnia oznacza w uproszczeniu, iż wysokim (bliskim maksi-mum) wartościom jednego czynnika
ryzyka odpowiadają w
współzależność ujemna oznacza w uproszczeniu, iż wysokim (bliskim maksi-mum) wartościom
jednego czynnika ryzyka, odpowiadają niskie (bliskie minimum) wartości drugiego czynnika
ryzyka. Ważnym aspektem pomiaru współzależności jest określenie prawdopodobieństwa warunkowego mierzonego współczynnikiem determinacji R2, stanowiącym współczynnik Pearson'a
podniesiony do kwadratu. Współczynnik R2, pozwala ocenić jakie jest prawdopodobieństwo, że
zmiana jednego czynnika ryzyka wywoła zmianę drugiego czynnika ryzyka.
Metody symulacyjne umożliwiają generowanie liczb losowych o zadanym natężeniu i kierun-ku
współzależności. Najprostszym rozwiązaniem jest dekompozycja Choleskiego dla standaryzowanych rozkładów normalnych (standaryzowany rozkład normalny, to rozkład normalny o
parametrach μ = 0; σ = 1). Dekompozycja dla przypadku dwuwymiarowego (dwóch zmien-nych
losowych; dwóch czynników ryzyka) przebiega następująco. Gdzie: xA, xB - współzależne liczby
losowe o standaryzowanym rozkładzie normalnym, zA, zB - niezależne liczby losowe o
standaryzowanym rozkładzie normalnym, ρ - współczynnik korelacji liniowej Pearson'a Efektem
dekompozycji są współzależne liczby losowe o standaryzowanym rozkładzie nor-malnym,
spełniające zadaną wartość współczynnika korelacji liniowej.
(…)
…, jeżeli xA, xB są współzależne) Uzyskane metodą inwersji prawdopodobieństwa zachowują w
przybliżeniu zadany współ-czynnik korelacji dla przypadków wielowymiarowych, oraz dokładnie dla przypadków dwuwymiarowych. Na podstawie współzależnych wartości prawdopodobieństwa,
możliwe jest wygenerowanie liczb o żądanym typie rozkładu i żądanych parametrach poprzez
funkcję odwrotną do funkcji dystrybuanty skumulowanego prawdopodobieństwa. Gdzie: Gy, Gv funkcje odwrotne rozkładów typu Y i V yA, yB - współzależne liczby o rozkładach typu Y i V
…
Statystyka - pytanie 66
Statystyka - pytanie 77
Statystyka - pytania i odpowiedzi na egzamin
ekonometria repetytorium
wzory statystyka-estymatory
Rachunek prawdopodobieństwa wykłady cz.2
Reklama































Prawa autorskie
Reklama
Kontakt