strategie gracza 1

Szkicowe rozwiązania i wskazówki dotyczące przykładowych zadań
Zbiór 1
Zadanie 1: strategie gracza 1: AF, AG, BF, BG; strategie gracza 2: C, D, E; równowagi Nasha w
strategiach czystych: (BF, C) oraz (BG, C)
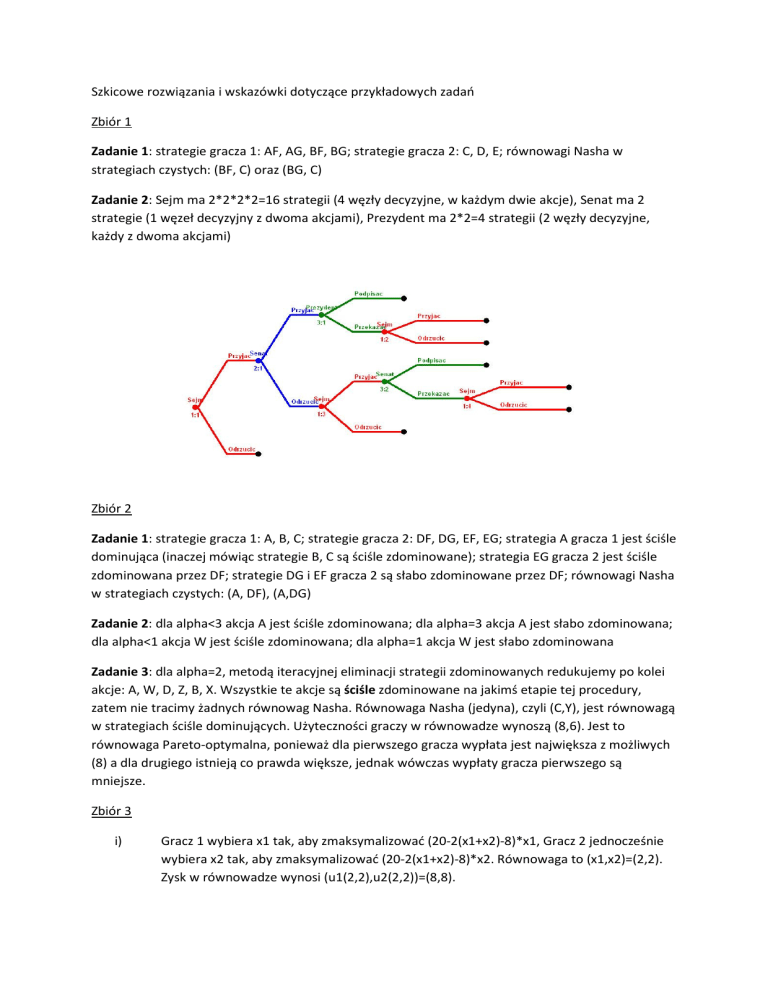
Zadanie 2: Sejm ma 2*2*2*2=16 strategii (4 węzły decyzyjne, w każdym dwie akcje), Senat ma 2
strategie (1 węzeł decyzyjny z dwoma akcjami), Prezydent ma 2*2=4 strategii (2 węzły decyzyjne,
każdy z dwoma akcjami)
Zbiór 2
Zadanie 1: strategie gracza 1: A, B, C; strategie gracza 2: DF, DG, EF, EG; strategia A gracza 1 jest ściśle
dominująca (inaczej mówiąc strategie B, C są ściśle zdominowane); strategia EG gracza 2 jest ściśle
zdominowana przez DF; strategie DG i EF gracza 2 są słabo zdominowane przez DF; równowagi Nasha
w strategiach czystych: (A, DF), (A,DG)
Zadanie 2: dla alpha<3 akcja A jest ściśle zdominowana; dla alpha=3 akcja A jest słabo zdominowana;
dla alpha<1 akcja W jest ściśle zdominowana; dla alpha=1 akcja W jest słabo zdominowana
Zadanie 3: dla alpha=2, metodą iteracyjnej eliminacji strategii zdominowanych redukujemy po kolei
akcje: A, W, D, Z, B, X. Wszystkie te akcje są ściśle zdominowane na jakimś etapie tej procedury,
zatem nie tracimy żadnych równowag Nasha. Równowaga Nasha (jedyna), czyli (C,Y), jest równowagą
w strategiach ściśle dominujących. Użyteczności graczy w równowadze wynoszą (8,6). Jest to
równowaga Pareto-optymalna, ponieważ dla pierwszego gracza wypłata jest największa z możliwych
(8) a dla drugiego istnieją co prawda większe, jednak wówczas wypłaty gracza pierwszego są
mniejsze.
Zbiór 3
i)
Gracz 1 wybiera x1 tak, aby zmaksymalizować (20-2(x1+x2)-8)*x1, Gracz 2 jednocześnie
wybiera x2 tak, aby zmaksymalizować (20-2(x1+x2)-8)*x2. Równowaga to (x1,x2)=(2,2).
Zysk w równowadze wynosi (u1(2,2),u2(2,2))=(8,8).
ii)
iii)
iv)
Indukcja wsteczna: gracz 2 wybiera x2 w zależności od x1 tak, aby zmaksymalizować (202(x1+x2)-8)*x2. Stąd otrzymujemy funkcję reakcji x2(x1)=3-0,5*x1. Teraz funkcję tą
wstawiamy do problemu optymalizacji gracza 1, który maksymalizuje w efekcie (po paru
przekształceniach) (6-x1)*x1 wybierając swój poziom produkcji x1. Wyliczamy optymalny
poziom x1=3 oraz x2(x1)=3/2. Zyski wynoszą odpowiednio 9 i 9/2.
Rozważamy (x1,x2)=(4,1). Łatwo można sprawdzić, że x2=1 jest najlepszą odpowiedzią
gracza 2 na x1=4 gracza 1, stąd wniosek, że graczowi 2 nie opłaca się odchodzić od
strategii x2=1, jeśli gracz 1 gra strategię x1=4. Teraz gracz 1 rozważa jednostronną zmianę
z x1=4 na coś innego. Jeśli zmniejszy swoją produkcję, wówczas gracz 2 wybierze x2=2 i
wtedy gracz 1 powinien wybrać x1=2 (najlepsza odpowiedź na x2=2). W tym wypadku
będzie miał zysk u1(2,2)=8, czyli tyle samo, ile u1(4,1) (czyli w najlepszym wypadku po
zmianie będzie miał tyle samo zysku co przed zmianą, dlatego zmiana się nie opłaca). Jeśli
natomiast zamiast zmniejszyć, gracz pierwszy będzie chciał zwiększyć swoją produkcję
powyżej 4, to gracz 2 wybierze x2=1,5. Najlepszą odpowiedzią gracza 1 na x2=1,5 jest
x1=2,25, czyli nie zwiększenie, ale zmniejszenie swojej produkcji. Dlatego para
(x1,x2)=(4,1) jest równowagą Nasha.
I graczowi 1 i graczowi 2 opłaca się zmienić poziom produkcji pod warunkiem, że
przeciwnik będzie grał tak, jak napisane w zadaniu. Na przykład, jeśli gracz 2 wybiera
x2=1,5 niezależnie od wszystkiego, wtedy gracz 1 powinien wybrać x1=2,25.
Zbiór 4
Zadanie 1: Równowaga doskonała w podgrach to (A,CF). Istnieje jeszcze jedna równowaga Nasha,
która nie jest doskonała w podgrach, mianowicie (B,DF). Jak łatwo zauważyć, żadnemu z graczy nie
opłaca się jednostronnie odejść od tej strategii. Równowaga nie jest doskonała, ponieważ, gracz 2
wybiera D w swoim lewym węźle decyzyjnym, ale tylko dlatego, że gracz 1 nie wybrał A i gracz 2 nie
musi rzeczywiście grać D, które, gdyby się rzeczywiście znalazł w lewym węźle, mu się wcale nie
opłaca. Czyli w podgrze z lewym węzłem decyzyjnym gracza 2 nie postępuje on optymalnie (D nie jest
równowagą Nasha tej małej podgry) - jednak (B,DF) jest równowagą Nasha całej gry ponieważ w tej
równowadze lewy węzeł decyzyjny nie zostanie w ogóle osiągnięty.
Zadanie 2: Są dwie równowagi doskonałe w podgrach w strategiach czystych: (AH, DG) oraz (BH, CG)
Zadanie 3: Są łącznie 3 równowagi doskonałe w podgrach – dwie w strategiach czystych i jedna w
strategiach mieszanych: (BG, DE), (AH, DF), (A(3/4G+1/4H),D(1/4E+3/4F)). Wskazówka – przedstaw w
formie strategicznej podgrę (nie całą grę) zaczynającą się od prawego węzła decyzyjnego gracza 2.
Wskaż tam trzy równowagi – 2 czyste i jedną mieszaną. Potem po kolei podstawiaj użyteczności z
tych trzech równowag jako liść w miejsce prawego węzła decyzyjnego gracza 2 – za każdym razem
znajdziesz jedną równowagę doskonałą w podgrach – łącznie 3.
Zbiór 5
Zadanie 1: Gracz 1 musi dać graczowi 2 przynajmniej tyle, żeby się zgodził na podział. W równowadze
doskonałej x=5/6 a y=1/6, bo pomimo, iż gracz 1 jest altruistą, to i tak woli mieć dla siebie niż dać
drugiemu.
Zadanie 2: Rozwiązanie Nasha: (11/4,13/6)