MATLOS-

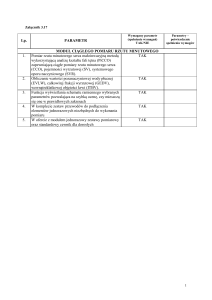
MATLOS
„JAK TEORIA MA SIĘ DO PRAKTYKI?”
Cel projektu:
Sprawdzamy, jaka jest
zależność między
prawdopodobieństwem
a częstością zdarzenia.
Słowniczek
Częstość zdarzenia - w pojedynczym doświadczeniu losowym
o zdarzeniu L (zdarzenie L może zajść lub nie) jest to iloraz l/n, gdzie
l - jest to liczba zajść zdarzenia L,
n - liczba powtórzeń doświadczenia.
Prawdopodobieństwo zdarzenia A - szansa zaistnienia określonego
zdarzenia obliczana zgodnie ze wzorem:
P(A)=n/N
gdzie:
n - to liczba zdarzeń sprzyjających
N- to liczba wszystkich możliwych zdarzeń
I doświadczenie – rzut monetą
Wykonaliśmy trzy doświadczenia – rzuciliśmy monetą 10
razy, 30 razy i 50 razy. Obliczyliśmy częstość
wystąpienia orła w każdym doświadczeniu. Otrzymane
wyniki porównaliśmy z prawdopodobieństwem
otrzymania orła w jednokrotnym rzucie monetą.
Następnie przeprowadziliśmy w programie Excel
symulację 500 oraz 1000 rzutów.
Nr rzutu
1
2
3
4
5
6
7
8
9
10
1 próba-wynik
R
R
R
O
R
R
R
R
O
R
Częstość =
𝟐
𝟏𝟎
Nr rzutu
1
2
3
4
5
6
7
8
9
10
11
2 próba-wynik
R
O
R
R
O
O
R
R
R
R
R
Nr rzutu
1
2
3
4
5
6
7
8
9
10
11
3 próba-wynik
R
R
O
O
R
O
R
O
O
R
R
Nr rzutu
31
32
33
34
35
36
37
38
39
40
41
3 próba-wynik
O
O
R
R
R
R
R
R
R
O
R
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
R
R
O
R
O
O
R
O
R
R
R
R
R
O
O
O
R
R
R
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
R
O
O
O
R
O
O
O
R
O
O
O
R
R
R
R
R
R
O
O
42
43
44
45
46
47
48
49
50
R
O
O
O
R
O
R
O
O
Częstość =
𝟏𝟎
𝟑𝟎
Częstość =
𝟐𝟒
𝟓𝟎
I doświadczenie – rzut monetą
Wniosek:
Im więcej prób, tym częstość zdarzenia jest
bliższa prawdopodobieństwu tego zdarzenia.
II doświadczenie – rzut kostką
Wykonaliśmy trzy doświadczenia –
rzuciliśmy sześcienną kostką do gry 10
razy, 30 razy i 50 razy. Obliczyliśmy
częstość wystąpienia szóstki w każdym
doświadczeniu. Otrzymane wyniki
porównaliśmy z prawdopodobieństwem
otrzymania szóstki w jednokrotnym
rzucie kostką.
Potem przeprowadziliśmy symulację dla
500 i 1000 rzutów.
Nr rzutu
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
1 próba-wynik
6
5
1
2
1
4
4
1
1
5
Częstość =
𝟏
𝟏𝟎
Nr rzutu
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
2 próba-wynik
5
1
5
1
3
1
2
2
6
2
Nr rzutu
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
3 próba-wynik
5
3
6
2
1
5
6
3
6
1
Nr rzutu
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
3 próba-wynik
2
3
5
6
4
6
3
4
6
4
11.
5
11.
1
41.
1
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
6
5
4
2
2
3
4
3
3
1
3
2
3
2
1
3
4
4
6
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
4
2
3
4
6
3
5
2
1
3
4
4
3
2
6
1
4
5
1
42.
43.
44.
45.
46.
47.
48.
49.
50.
3
2
5
6
5
4
4
6
3
Częstość =
𝟑
𝟑𝟎
Częstość =
𝟗
𝟓𝟎
II doświadczenie – rzut kostką
Wniosek:
Im więcej prób, tym
częstość zdarzenia
jest bliższa
prawdopodobieństwu
tego zdarzenia.
III doświadczenie - karty
Z talii 52 kart dokonaliśmy 50 razy losowania karty
(po każdym losowaniu odkładaliśmy kartę do talii
i tasowaliśmy karty). Obliczyliśmy:
 częstość wylosowania asa
i prawdopodobieństwo wylosowania asa,
 częstość wylosowania kiera
i prawdopodobieństwo wylosowania kiera,
 częstość wylosowania figury
i prawdopodobieństwo wylosowania figury.
III doświadczenie - karty
Wniosek:
Im więcej prób, tym
częstość zdarzenia jest
bliższa
prawdopodobieństwu tego
zdarzenia.
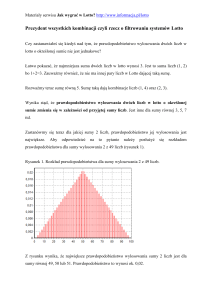
Lotto
Po sprawdzeniu częstości wypadania
poszczególnych liczb w całej historii losowania
Lotto okazało się, że procent wystąpień każdej
z nich jest prawie równy.
Lotto
Po sprawdzeniu
prawdopodobieństwa
trafienia określonej ilości
liczb spośród
wytypowanych,
otrzymaliśmy zestawienie:
prawdopodobieństwo
wygranej
Liczby
lotto
6 0,00000007
5 0,00002
4 0,001
3 0,02
2 0,13
1 0,42
0 0,43
jakakolwiek 0,02
wygrana
Lotto
Na stronie internetowej Lotto typowaliśmy swoje
„szczęśliwe szóstki”. Jedna osoba trafiła za szóstym
razem, inna za jedenastym, jeszcze inna podjęła ponad
trzydzieści prób i nie udało jej się trafić. Wniosek z tego
taki, że mimo to że prawdopodobieństwo trafienia szóstki
w lotto jest równe w przybliżeniu 0 (czyli prawie
niemożliwe), to zawsze znajdzie się „szczęściarz’’,
któremu to się uda.
Lotto
W historii losowań Lotto było
kilka szóstek, które wypadły
dwa razy. Zdarzył się także
przypadek, gdy takie same
liczby zostały wylosowane
dwa razy zrzędu (np.
4,15,23,34,35,42).
Podsumowanie
Wnioski ze wszystkich przeprowadzonych
doświadczeń są następujące:
Im więcej przeprowadzonych prób
doświadczenia, tym bardziej częstość
zdarzenia jest bliższa prawdopodobieństwu
tego zdarzenia. Jest to tzw. Prawo Wielkich
Liczb.
Dziękujemy za uwagę
Julia Nizio
Tomasz Fornala
Radosław Przybyło