Rezonans w obwodach elektrycznych

Rezonans w obwodach
elektrycznych
Patryk Sobczyk
Pojęcie rezonansu
Rezonans jest to taki stan pracy obwodu
elektrycznego, w którym reaktancja wypadkowa
obwodu lub jego susceptancja (przewodność
bierna) wypadkowa jest równa zeru.
Obwodami rezonansowymi są nazywane obwody
elektryczne, w którym występuje zjawisko
rezonansu.
Właściwości rezonansu
W stanie rezonansu napięcie i prąd
na
zaciskach
rozpatrywanego
obwodu są zgodne w fazie, tzn.
argument impedancji zespolonej
obwodu lub admitancji zespolonej
jest równy zeru (=0).
Właściwości rezonansu
Obwód będący w stanie rezonansu nie pobiera ze
źródła mocy biernej, a mówiąc ściśle następuje
zjawisko kompensacji mocy. Moc bierna
indukcyjna pobierana przez obwód jest równa
mocy biernej pojemnościowej. Ponieważ, jak
wiadomo, znaki mocy biernej, indukcyjnej i
pojemnościowej są przeciwne, dlatego w
warunkach rezonansu całkowita moc bierna
obwodu też jest równa zeru.
Właściwości rezonansu
Częstotliwość, przy której reaktancja wypadkowa
lub susceptancja wypadkowa obwodu jest równa
zeru, jest nazywana częstotliwością rezonansową i
oznaczana fr. Obwód elektryczny osiąga stan
rezonansu, jeśli częstotliwość doprowadzonego do
obwodu napięcia sinusoidalnego jest równa
częstotliwości rezonansowej.
W zależności od sposobu połączenia elementów R,
L, C, w obwodzie może wystąpić zjawisko
rezonansu napięć lub zjawisko rezonansu prądów.
Wielkości charakteryzujące rezonans
Impedancja falowa ρ. Nazywamy tak reaktancję
indukcyjną lub pojemnościową obwodu przy
częstotliwości rezonansowej, czyli:
L

C
Wielkości charakteryzujące rezonans
Dobroć wyrażona wzorem:
UL UC IL IC
Q

 
UR UR IR IR
oraz uwzględniając impedancję falową:
w przypadku
rezonansu napięć:
Q

R
w przypadku
rezonansu prądów:
Q
R

Wielkości charakteryzujące rezonans
Reaktancja obwodu szeregowego RLC wyrażana
wzorem:
1
X L
C
.
.
Wielkości charakteryzujące rezonans
Częstotliwość, występujący w czasie rezonansu,
nazywa się częstotliwością
rezonansową
szeregowego obwodu rezonansowego. Wyrażana
jest ona wzorem:
fr 
1
2 LC
Rezonans napięć
Rezonans występujący w obwodzie o szeregowym
połączeniu elementów R, L, C, charakteryzujący się
równością reaktancji indukcyjnej i reaktancji
pojemnościowej nazywamy rezonansem napięć lub
rezonansem szeregowym.
Rezonans napięć
Załóżmy, że do dwójnika szeregowego RLC
doprowadzono napięcie sinusoidalne o wartości
skutecznej zespolonej równej U i o pulsacji = 2πf.
Dla rozpatrywanego obwodu słuszne są zależności:
a) UR=RI
b) UL=jXLI
c) UC=-jXCI
Rezonans napięć
Zgodnie z podaną definicją, rezonans napięć
wystąpi wówczas, gdy X=0, tzn.:
XL  XC
Inaczej:
1
L
C
.
.
Rezonans napięć
W stanie rezonansu szeregowego słuszne są więc
następujące zależności:
a) Z=R
b) U=UR
c) UL+UC =0
d) UL=UC
Rezonans napięć
Opisując słownie można stwierdzić że:
a) reaktancja pojemnościowa równa się reaktancji
indukcyjnej
b) impedancja obwodu jest równa rezystancji, a zatem
argument impedancji zespolonej jest równy zeru, a
oznacza iż wartość współczynnika mocy cos  =1
c) napięcie na indukcyjności jest równe co do modułu
napięciu na pojemności, a suma geometryczna tych
napięć jest równa zeru
d) wobec X=0, prąd w obwodzie może osiągnąć bardzo
dużą wartość, gdyż przy małej rezystancji R, źródło
pracuje w warunkach zbliżonych do stanu zwarcia
Rezonans napięć
W stanie rezonansu napięcie na rezystancji jest równe
napięciu doprowadzonemu do obwodu, tzn. UR=U. Z
tego wynika, że dobroć obwodu Q określa, ile razy
napięcie na indukcyjności lub napięcie na pojemności
jest większe od napięcia na zaciskach obwodu.
Jeśli rezystancja obwodu rezonansowego jest mała, to
dobroć obwodu jest duża i napięcie na elementach
reaktancyjnych znacznie przekracza wartość napięcia
doprowadzonego. Należy więc liczyć się ze zjawiskiem
przepięcia.
Rezonans prądów
Rezonans występujący w obwodzie o równoległym
połączeniu elementów R, L, C charakteryzujący się
równością susceptancji indukcyjnej i susceptancji
pojemnościowej, nazywamy rezonansem prądów
lub rezonansem równoległym.
Rezonans prądów
Załóżmy, że do dwójnika równoległego RLC
doprowadzono napięcie sinusoidalne o wartości
skutecznej zespolonej U i o pulsacji =2πf . Dla
rozpatrywanego obwodu są słuszne następujące
zależności:
a) IR= GU
b) IL=-jBLU
c) IC=jBCU
Rezonans prądów
Zgodnie z podana definicją, rezonans prądów
wystąpi wówczas, gdy B=0, tzn. że:
Inaczej:
BC  BL
1
C 
L
.
.
Rezonans prądów
W stanie rezonansu, z równoległą pojemnością
połączoną
szeregowo
z
rezystancją
oraz
indukcyjnością połączoną szeregowo z rezystancją,
zachodzącego w obwodzie są słuszne następujące
zależności:
a) Y=G
b) I=IR
c) IL+IC=0
d) IL=IC
Rezonans prądów
Opisując słownie:
a) susceptancja pojemnościowa jest równa susceptancji
indukcyjnej
b) admitancja obwodu jest równa konduktancji, a zatem
argument admitancji zespolonej jest równy zeru , czyli
cos =1
c) prąd w gałęzi indukcyjnej jest równy co do modułu
prądowi
w
gałęzi
pojemnościowej,
a
suma
geometryczna tych prądów jest równa zeru
d) wobec B=0, prąd całkowity ma bardzo małą wartość, a
przy bardzo małej konduktancji jest prawie równy zeru i
źródło pracuje w warunkach zbliżonych do stanu
jałowego.
Rezonans prądów
Wobec tego z zależności określającej dobroć obwodu
rezonansowego wynika, że dobroć obwodu Q określa ,
ile razy prąd w gałęzi z indukcyjnością lub w gałęzi z
pojemnością jest większy od prądu dopływającego do
obwodu rezonansowego.
Jeżeli rezystancja obwodu R jest duża (konduktancja G
mała), to dobroć obwodu jest duża i prądy w gałęziach
reaktancyjnych znacznie przekraczają wartość prądu
dopływającego do obwodu. Należy więc się liczyć ze
zjawiskiem przetężenia.
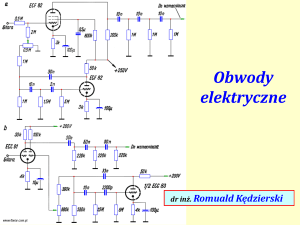
Przykłady obwodów rezonansowych
Przykłady obwodów rezonansowych
Opis obwodów
Schemat przedstawiony po lewej stronie slajdu 22
przedstawia
obwód
rezonansowy
szeregowy
(napięciowy)
oraz równoległy (prądowy). Drugi
schemat po prawej stronie przedstawia równoległy
rezonans wraz z przebiegiem impedancji w nim
zachodzącym. W slajdzie 23 po lewej stronie schemat
przedstawia schemat anteny w odbiorniku „Pionier”
superheterodynowym.
Po
prawej
stronie
przedstawiony został schemat generatora Hartleya w
konfiguracji WE. W ostatnim wymienionym slajdzie
właściwe obwody rezonansowe zostały zaznaczone
czerwonym prostokątem.
Źródła:
1. http://www.zsl.gda.pl/~mp/klasy_2/sala%20149/Badanie%20dwojnikow%20RLC/obwody%
20rezonansowe/Rezonans%20w%20obwodach%20elektrycznych.doc
2. http://www.noss.yoyo.pl/noss/elektronika/elektronika/pe360/pe360_2.png
3. http://www.zgapa.pl/zgapedia/data_pictures/_uploads_wiki/o/obwod_rezonansowy.png
4. http://oldradio.pl/img/pionier/ow2.jpg
5. http://www.eres.alpha.pl/elektronika/fusion_images/elektronika/generatory7.gif
6. http://www.eres.alpha.pl/elektronika/fusion_images/elektronika/generatory9.gif