analiza wariancji

Testy analizy wariancji pozwalają sprawdzić
czy pewne czynniki wywierają wpływ na
kształtowanie się średnich wartości badanych
cech. W teście analizy wariancji dla
klasyfikacji pojedynczej bada się wpływ tylko
jednego czynnika na wyniki obserwacji
badanej cechy.
Procedura testu analizy wariancji jest
następująca:
Mając dane k populacji o rozkładzie
normalnym lub o rozkładzie zbliżonym do
rozkładu normalnego zakłada się, że
wariancje wszystkich k populacji są równe
(ale nie muszą być znane). Jednorodność
wariancji wszystkich populacji można badać
jednym z testów jednorodności wariancji np.
testem Hartleya.
Następnie z każdej z tych populacji należy
wylosować niezależne próby o liczebności ni
elementów. Wyniki z prób oznaczane są
przez xij , gdzie i = 1,2,...,k, a j = 1,2,...,ni,
przy czym
x  m 
ij
i
ij
gdzie  ij oznacza składnik losowy, mający
rozkład N (0,  ).
Na podstawie wyników należy zweryfikować
hipotezę zakładającą równość średnich
wszystkich badanych populacji:
H 0 : m1  m2  ...  mk
wobec hipotezy alternatywnej:
H1 : m1  m2  ...  mk
W celu zweryfikowania tej hipotezy należy
obliczyć z wyników poszczególnych prób
średnie grupowe
xi
i średnią ogólną
x
według poniższych wzorów:
1
xi 
ni
ni
x
j 1
ij
dla i  1, 2, ..., k
k
1 k ni
x   xij gdzie n   ni
n i 1 j 1
i 1
Test analizy wariancji przebiega według
schematu, ujętego w postaci tablicy analizy
wariancji, która wygląda w następujący
sposób:
Źródło
Suma
zmienności
kwadratów
Między
k
2
populacjami  ( x i  x) ni
i 1
(grupami)
Wewnątrz
k n
grup (składnik  ( xij  x i ) 2
i 1 j 1
losowy)
Stopnie
swobody
k-1
i
n-k
Wariancja
Test F
^2
s1
^2
s2
^2
F
s1
^2
s2
gdzie:
k
^2
s1 
2
(
x

x
)
ni
 i
i 1
k 1
k
^2
s2 
ni
2
(
x

x
)
i
 ij
i 1 j 1
nk
Wartość statystyki F porównujemy z wartością
krytyczną F,k-1,n-k odczytaną z tablic
rozkładu F-Snedecora dla ustalonego
poziomu istotności  i dla odpowiedniej
liczby stopni swobody k-1 i n-k.
Jeżeli F  F,k-1,n-k, to hipotezę H0 o równości
średnich w badanych populacjach należy
odrzucić.
Natomiast, gdy F < F,k-1,n-k, to nie ma
podstaw do odrzucenia hipotezy H0.
Odrzucenie hipotezy zerowej oznacza
udowodnienie istotnego wpływu podziału na
badane populacje. W przeciwnym przypadku
wszystkie populacje można uznać za
równoważne z punktu widzenia
otrzymywanych wartości badanej cechy.
Test Hartleya jest jednym z testów
jednorodności wariancji. Służy on do
sprawdzenia równości wariancji wielu (k)
populacji. Test jednorodności wariancji
wykorzystuje się najczęściej jako zagadnienie
pomocnicze przy badaniu analizy wariancji.
Test Hartleya stosuje się w przypadku
równolicznych prób.
Hipoteza zerowa i hipoteza alternatywna
testu Hartleya mają następującą postać:
H 0 :   ...  
2
k
H1 :   ...  
2
k
2
1
2
1
Statystyka testu Hartleya przyjmuje postać:
Fmax
2
max
2
min
s

s
Wzór na wariancję populacji ma postać:
ni
si2 
2
(
x

x
)
 i i
i 1
ni
Statystykę testu Hartleya Fmax porównuje się z
wartością krytyczną odczytaną z tablic
wartości krytycznych w teście Hartleya
fmax(, k, n). Gdzie  oznacza poziom
istotności, a k i n liczbę stopni swobody.
Jeżeli Fmax > fmax(, k, n), to istnieją podstawy
do odrzucenia hipotezy zerowej,
w przeciwnym wypadku nie ma podstaw do
odrzucenia hipotezy zerowej.
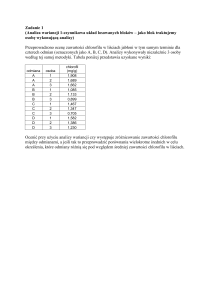
W poniższej tabeli zostały przedstawione
wyniki egzaminu ze statystyki otrzymane
przez studentów trzech różnych grup:
Grupa 1
Grupa 2
Grupa 3
90
88
87
84
85
83
82
84
80
81
76
78
78
74
75
76
72
69
69
67
60
Należy zweryfikować hipotezę (na poziomie
istotności 0,05), że czynnik jakim jest
przynależność do grupy wykładowej znacząco
różnicuje uzyskaną liczbę punktów z
egzaminu ze statystyki 