Hipoteza statystyczna
Hipoteza statystyczna - przypuszczenie dotycz ce rozkładu populacji
Rodzaje hipotez:
podział I
• parametryczne - dotycz warto ci parametru rozkładu np. wariancje dwóch populacji o
rozkładzie normalnym s sobie równe
• nieparametryczne - dotycz postaci funkcyjnej rozkładu populacji np.: populacja
generalna ma rozkład Poissona
podział II
• proste - hipotezy, które jednoznacznie specyfikuj rozkład populacji generalnej np.:
parametr λ w rozkładzie Poissona jest równy 3 (hipotez równie parametryczna)
• zło one - hipotezy, które niejednoznacznie specyfikuj rozkład populacji generalnej np.:
wariancja populacji generalnej jest wi ksza od 5
przy weryfikacji hipotez:
• hipoteza zerowa (H0) - bezpo rednio sprawdzana
• hipoteza alternatywna (H1) - hipoteza konkurencyjna do hipotezy H0.
(H0: m=2; H1:m=5); (H0: p=0.3; H1: p>0.3); (H0: f(x)=f0(x); H1:f(x) ≠ f1(x))
Metody probabilistyczne i statystyka
Wykład 3: Weryfikacja hipotez.
Testy istotno ci
Małgorzata Kr towska
Wydział Informatyki
Politechnika Białostocka
e-mail: [email protected]
Modele statystyczne (studia zaoczne)
1
Modele statystyczne (studia zaoczne)
Weryfikacja hipotez
2
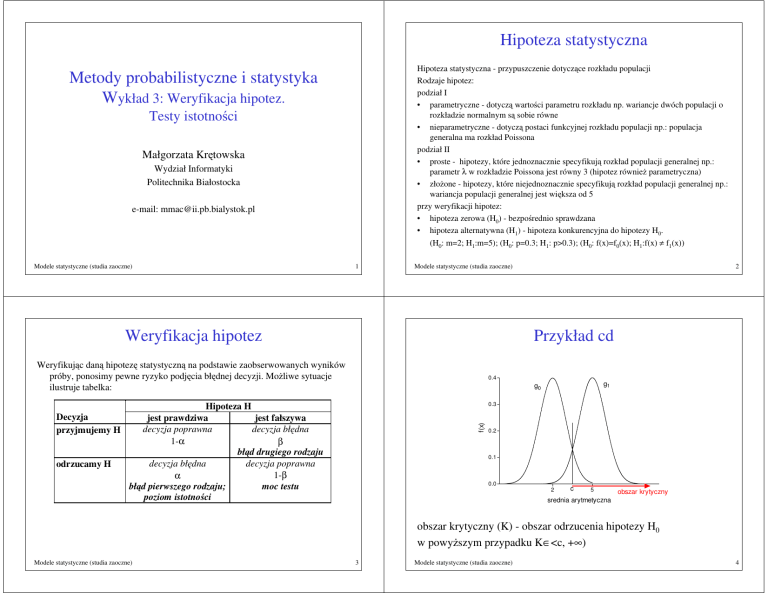
Przykład cd
Weryfikuj c dan hipotez statystyczn na podstawie zaobserwowanych wyników
próby, ponosimy pewne ryzyko podj cia bł dnej decyzji. Mo liwe sytuacje
ilustruje tabelka:
0.4
g1
g0
Hipoteza H
Decyzja
jest prawdziwa
jest fałszywa
decyzja poprawna
decyzja bł dna
przyjmujemy H
1-α
β
bł d drugiego rodzaju
decyzja bł dna
decyzja poprawna
odrzucamy H
1-β
α
moc testu
bł d pierwszego rodzaju;
poziom istotno ci
f(x)
0.3
0.2
0.1
0.0
2
c
5
srednia arytmetyczna
obszar krytyczny
obszar krytyczny (K) - obszar odrzucenia hipotezy H0
w powy szym przypadku K∈<c, +∞)
Modele statystyczne (studia zaoczne)
3
Modele statystyczne (studia zaoczne)
4
Zale no bł dów I i II rodzaju
od liczno ci próby
Przykład cd
0.4
0.4
g1
g0
g1
0.2
f(x)
0.2
0.3
f(x)
g0
f(x)
0.5
0.1
0.1
2
0.0
β c α 5
1-α
α
2
c
5
g1
0.2
0.0
0.0
1-β
β
x ~ N m,
gdzie Zn - statystyka z próby
Modele statystyczne (studia zaoczne)
5
Testy istotno ci
5
srednia arytmetyczna
X~N(m,8)
n=16
1-α=P(Zn∉K/H0)
1- β=P(Zn∈K/H1)
c
2
c 5
srednia arytmetyczna
2
srednia arytmetyczna
srednia arytmetyczna
α=P(Zn∈K/H0)
β=P(Zn∉K/H1)
g0
0.1
X~N(m,8)
n=64
8
= N (m,2 )
16
x ~ N m,
8
= N (m,1)
64
Modele statystyczne (studia zaoczne)
6
Testowane hipotezy i obszary krytyczne
W praktyce wykorzystuje si testy, w których nie oblicza si bł du II rodzaju. Test
buduje si w ten sposób, aby zagwarantowa mał warto bł du I rodzaju,
dan z góry jako poziom istotno ci α. S to testy istotno ci.
Postaci hipotez w testach istotno ci:
Budowa testu istotno ci:
1. Ustalenie postaci hipotezy zerowej H0 i hipotezy alternatywnej H1
2. Wyznaczenie statystyki Zn z próby
3. Okre lenie obszaru krytycznego (K) przy danym poziomie istotno ci α
4. Sprawdzenie czy statystyka Zn nale y do obszaru krytycznego K
5. Sformułowanie wniosku:
– odrzuceniu hipotezy H0 na korzy H1 (przyj cie hipotezy H1)
– brak podstaw do odrzucenie hipotezy H0
H0: θ = θ0
(θ - parametr rozkładu populacji generalnej)
H1: θ ≠ θ0;
H1: θ > θ0;
H1: θ ≠ θ0
H1: θ < θ0
1.0
H0: θ = θ0
f(x)
f(x)
0.4
1.0
0.3
0.3
0.0
g1
g0
0.5
g0
α/2
α/2
0.0
Zn
obszar krytyczny dwustronny
Modele statystyczne (studia zaoczne)
7
Modele statystyczne (studia zaoczne)
8
Wnioskowanie w testach istotno ci
Testowane hipotezy i obszary krytyczne
H0: θ = θ0
H0: θ = θ0
H1: θ > θ0
H1: θ < θ0
1.0
α
0.0
0.5
g0
1.0
0.0
Zn
0.5
Zn
obszar krytyczny prawostrony
Modele statystyczne (studia zaoczne)
9
Warto
f(x)
f(x)
1.0
α
0.0
Zn
0.5
α
0.0
uα
uα
Zn
Modele statystyczne (studia zaoczne)
p (p-value)
g0
0.5
α
g0
obszar krytyczny lewostronny
0.0
1.0
1.0
g0
α
f(x)
0.5
statystyki z próby Zn nale y do obszaru krytycznego:
Zn ∈K => odrzucamy H0 na korzy hipotezy H1
(przyjmujemy H1)
• je eli warto statystyki z próby Zn nie nale y do obszaru krytycznego:
Zn ∉K => brak podstaw do odrzucenia hipotezy H0
(co nie jest jednoznaczne z przyj ciem H0)
Ad 1)
Ad 2)
f(x)
g0
f(x)
f(x)
1.0
• je eli warto
10
Testy dla warto ci redniej
g0
Postaci hipotez:
H0: m=m0
H1: m≠m0;
0.5
m>m0;
m<m0;
p
0.0
uα
α=P(Z < uα)
gdzie uα- warto
Model 1
Zało enia: próba losowa pobrana z populacji o rozkładzie N(m, σ); σ jest znane;
Zn
Estymator parametru m:
p=P(Z<Zn)
graniczna obszaru K
Zn – statystyka z próby
1
n
n
i =1
xi ~ N m,
σ
n
σ
Wnioskowanie:
je eli p ≤ α => odrzucamy H0 na korzy H1
je eli p>α => brak podstaw do odrzucenia hipotezy H0
Przy zało eniu prawdziwo ci hipotezy H0: x ~ N m0 ,
n
Standaryzuj c otrzymujemy statystyk U:
Warto p - najmniejszy poziom istotno ci, przy którym zaobserwowana
warto statystyki testowej prowadzi do odrzucenia hipotezy zerowej.
Modele statystyczne (studia zaoczne)
x=
U=
która ma rozkład N(0,1).
11
Modele statystyczne (studia zaoczne)
x − m0
σ
n
12
Testy dla warto ci redniej
Testy dla warto ci redniej
Model 2
Zało enia: próba losowa pobrana z populacji o rozkładzie N(m, σ); σ jest
nieznane; liczno próby mała (n ≤ 30)
Model 3
Zało enia: próba losowa pobrana z populacji o rozkładzie N(m, σ); σ jest
nieznane; liczno próby duza (n > 30)
Przy estymacji warto ci m korzystamy ze statystyki t Studenta z n-1 stopniami
swobody:
X −m
1 n
t=
n −1
s
=
( xi − X ) 2
s
n
Estymator parametru m:
Modele statystyczne (studia zaoczne)
n −1 =
X − m0
sˆ
n
sˆ =
n
i =1
xi ~ N m,
s
n
s
Przy zało eniu prawdziwo ci hipotezy H0, otrzymujemy:
X − m0
s
1
n
Przy zało eniu prawdziwo ci hipotezy H0: x ~ N m0 ,
n
Standaryzuj c otrzymujemy statystyk U:
i =1
t=
x=
U=
1 n
( xi − X ) 2
n − 1 i =1
x − m0
s
n
która ma rozkład N(0,1).
13
Modele statystyczne (studia zaoczne)
14












